Особенности преподавания математики в условиях введения
ФГОС ООО
Цели и задачи обучения математике в соответствии с ФГОС.
Математическое образование в системе общего среднего образования занимает одно из ведущих мест, что определяется безусловной практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности. Целью обучения математике является наряду с изучением собственно математики развитие универсальных (общих) способностей, умений и навыков, являющихся основой существования человека в социуме.
В результате изучения предметной области «Математика и информатика» (в нее входит учебный предмет «Математика») обучающиеся развивают логическое и математическое мышление, получают представление о математических моделях; овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты; овладевают умениями решения учебных задач; развивают математическую интуицию. Содержание математического образования основной школы формируется на основе Фундаментального ядра школьного математического образования. Оно представлено в виде следующих содержательных разделов: арифметика; алгебра; функции; вероятность и статистика; геометрия. Наряду с этим включены два дополнительных блока: логика и множества; математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся.
2. Особенности организации обучения математике в соответствии с ФГОС.
Очевидно, что новые требования к результатам образовательной деятельности требуют определенных изменений в содержании и организации процесса обучения.
Проектирование УУД в календарно-тематическом планировании представляется принципиально новым элементом деятельности учителя. Каждый учебный предмет раскрывает определенные возможности для формирования УУД. УУД вполне может выступать в качестве предмета обучения; выделяться в тематическом планировании каждого раздела учебной дисциплины и уточняться поурочно в календарно-тематическом планировании. В общем случае УУД должно являться инструментом или способом достижения цели и задач каждого урока. При этом учителю необходимо владеть видами и содержанием каждого из УУД и знать связи между ними.
Действия учителя при планировании учебного занятия:
Выбор УУД в соответствии с целью урока, содержанием учебного материала, технологиями обучения, спецификой учебного предмета, возрастными особенностями учащихся.
Выделение времени для формирования и/или развития УУД в границах учебного занятия или урока.
Определение приемов, методов, способов и форм организации деятельности учащихся для формирования и/или развития УУД.
Проектирование содержания деятельности учащихся для формирования и/или развития УУД через использование системы разнообразных задач и средств их решения.
Еще одной существенной задачей для учителя становится определение ресурсов своего предмета в формировании и совершенствовании УУД: в каких учебных темах, какими средствами формировать те или иные УУД.
Универсальные учебные действия - способность субъекта к саморазвитию путем сознательного, активного присвоения нового социального опыта. Различают 4 вида универсальных учебных действий:
личностные;
регулятивные;
коммуникативные;
познавательные.
Конкретизируем содержание УУД, которые формируются на уроках математики. Следует отметить, что предмет «Математика» направлен, прежде всего, на развитие познавательных универсальных учебных действий. Итак, познавательные УУД:
Общеучебные: построение устных и письменных высказываний, работа с информацией, целеполагание, структурирование знаний, рефлексия, контроль, оценка, создание алгоритмов деятельности, выбор эффективных способов решений.
Логические: формирование понятий, сравнение, сериация, установление причинно-следственных связей, построение логической цепочки, выдвижение гипотез и их доказательство, анализ, синтез, осознание, что такое свойства предмета, умение приводить контрпримеры.
Знаково-символические: замещение, кодирование, декодирование, моделирование, использование знаково-символической записи математического понятия.
Постановка и решение проблемы: формулирование проблемы, создание способов решения проблемы, использование индуктивного умозаключения.
Формирование универсальных учебных действий и является задачей на каждом этапе урока.
Обязательным элементом урока в системно-деятельностном подходе является учебная проблема:
учитель может лично заострить противоречие и сообщить учебную проблему;
учащиеся совершенно самостоятельно осознают противоречие и формулируют проблему;
учитель в диалоге побуждает учеников осознать противоречие и сформулировать учебную проблему.
Т.е. как советует доктор психологических наук Галина Анатольевна Цукерман: «Не давать образцов, ставить ребенка в ситуацию, где его привычные способы действия с очевидностью непригодны, мотивировать поиск существенных особенностей новой ситуации, в которой надо действовать»
3. Структура урока математики по технологии системно-деятельностного подхода
1. Мотивация к учебной деятельности.
Создание настроя и задание мотивации на урок, причины для учёбы, связанной с семантикой ребёнка.
Способы мотивации деятельности детей: вопросы, суждения, ошибки персонажей; задания, для выполнения которых недостаёт знаний; заголовки-вопросы; наблюдения за фактами, в том числе за ошибками, для объяснения которых нужны новые сведения, и др. Учебным действием является лишь то действие, которое «цепляет» ум ученика.
Примеры:
На предыдущем уроке мы делили 28 конфет на 25 человек, и 3 конфеты у нас было в остатке, а сегодня нам нужно одну конфету разделить на двоих, одну шоколадку на троих. Как это сделать?
Пирог, который мама испекла на день рождения Малыша, Карлсон предложил разделить следующим образом: 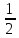 часть Карлсону, а
часть Карлсону, а 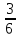 - всем остальным. Как вы считаете, все ли получат поровну?
- всем остальным. Как вы считаете, все ли получат поровну?
Перед уроком по знакомству с понятием «процент» прошу детей быть очень внимательными один день и посчитать, сколько раз за этот день они услышали или прочитали слово «процент».
2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии
Актуализация изученных способов действий, достаточных для построения нового знания, их обобщение и звуковая фиксация.
Примеры:
Проговаривание, на сколько частей будем делить конфету; на сколько частей шоколадку, какие части получим (половина, треть).
Как выяснить, корректно ли поступает Карлсон? (сравнить 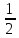 и
и 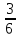 ).
).
После выяснения того, как часто дети встретились со словом «процент» идёт беседа о частях целого и проценте - как сотой части от целого.
3.Выявление места и причины затруднения.
Учащиеся должны восстановить выполненные операции и зафиксировать (вербально и знаково) место, шаг, операцию, где возникло затруднение; соотнести свои действия с используемым способом действий и на этой основе выявить и зафиксировать во внешней речи причину затруднения.
Примеры:
1 (целую конфету или шоколадку) надо разделить на несколько частей, в жизни можно разломить или разрезать, а как в математике?
Как сравнить 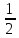 и
и 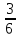 ?
?
Почему берётся именно сотая часть от целого и как это фиксируется на математическом языке?
4. Построение проекта выхода из затруднения.
Использование ошибки на пользу себе и ученику. Ошибка - не неудача, ошибка - это обратная связь, актуализация соответствующих мыслительных операций и познавательных процессов; мотивация к пробному учебному действию («надо» - «могу» - «хочу») и его самостоятельное осуществление; фиксация индивидуальных затруднений в выполнении пробного учебного действия или его обоснования.
Примеры:
Делим целую конфету на две части, каждому достаётся по одной из двух частей; по одной из трёх частей от шоколадки.
Подвод учащихся к тому, что надо в обеих дробях иметь одинаковый знаменатель.
Историческая справка (может быть подготовлена учащимся) о происхождении слова «процент» и знака процента.
Реализация построенного проекта.
Использование на уроке лево-правополушарного подхода. Структурирование учебной информации: дробление, укрупнение, дети учатся переводить текстовую информацию в изобразительную и наоборот. Процесс восприятия информации - процесс сугубо индивидуальный и прежде чем ребенок выйдет на уровень парной, групповой или фронтальной работы, ему необходимо предоставить возможность индивидуально осмыслить учебную информацию в любом ее виде.
Примеры:
Нарисовать целую конфету и целую шоколадку и разделённые на части, подписать. Сделать вывод о делении целого на части, математической записи (понятие дроби, числителя, знаменателя)
Нарисовать пирог, разделенный на б частей. Раскрасить разными цветами. Сделать вывод о том, как изобразить 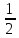 часть пирога, а как -
часть пирога, а как - 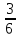 и как из одной дроби получается другая. Вывести и сформулировать правило сокращения дроби и правило приведения дроби к общему знаменателю.
и как из одной дроби получается другая. Вывести и сформулировать правило сокращения дроби и правило приведения дроби к общему знаменателю.
Изобразить 100% в виде круга, закрасить разные его части, выраженные в процентах. Сделать вывод о соотношении частей и процентов.
Первичное закрепление с проговариваиием во внешней речи.
Эффективность учебно-познавательной деятельности учащихся резко повышается с использованием на уроке полимодальной (визуалы, аудиалы, кинестеты) речи: словесные 10% - 20% (слышит), наглядные 50% (видит), практические 90% (делает сам).
Скажи мне, я забываю. Покажи мне, я могу запомнить. Позволь мне сделать это, и это станет моим навсегда (Китайская пословица).
Примеры:
Работа в парах по чтению дробей, проговариванию числителя и знаменателя, по записи частного в виде дроби, выполнению рисунков, нахождению разных способов записи закрашенных частей фигур и не закрашенных.
Работа по сокращению дробей, приведению дробей к общему знаменателю, выполнению рисунков.
Работа по переводу процентов в части, частей в проценты, изображению на рисунках, схемах.
Самостоятельная работа с самопроверкой по эталону.
Сравнивание успехов ученика с его собственным прошлым состоянием, а не с успехами другого.
Включение в систему знаний и повторение.
Поддержание группового раппорта с классом и индивидуального раппорта с каждым учеником. (Раппорт - процесс построения и поддержания отношений взаимного доверия между двумя и более людьми).
Примеры:
Дифференцированная работа с учащимися по освоению понятия: «дробь».
Работа по применению правил сокращения дробей и приведению дробей к общему знаменателю.
Работа в группах по решению задач с процентами.
9. Рефлексия учебной деятельности на уроке.
Фиксируется новое содержание, изученное на уроке, организуется рефлексия и самооценка учениками собственной учебной деятельности. Соотносятся ее цель и результаты, намечаются дальнейшие цели деятельности. Проведение так называемой подстройки к будущему (соединить изученный на уроке материал с уже имеющимся в голове у ученика и сориентировать на восприятие будущего нового материала)
Примеры:
На уроке мы делили целое на части, узнали новую форму записи чисел - дробь, что она означает. А на следующем уроке мы научимся находить целое по его части, а так же часть от целого.
На уроке мы узнали основное свойство дроби, научились сокращать дроби и приводить их к общему знаменателю. Мы работали с дробями, у которых числитель меньше знаменателя, а на следующем уроке мы будем работать с дробями, у которых числитель больше знаменателя и узнаем, как они называются.
На уроке мы узнали что такое «процент», а на следующем уроке мы научимся решать задачи на проценты и узнаем, как они помогают нам в жизни.
Исследовательский метод – высший уровень проблемного подхода. Проблемное изложение и проблемная беседа являются подготовкой учащихся к нему. Исследовательский метод в обучении заключается в самостоятельном решении учащимися проблем, трудных задач познавательного и практического характера. При исследовательской деятельности дети отыскивают не только способы решения поставленных проблем, но и побуждаются к самостоятельной их постановке, к выдвижению целей своей деятельности. В качестве примера применения данного метода можно привести исследовательскую работу при изучении темы «Длина окружности и площадь круга» в 6 классе. В результате своей деятельности обучающиеся приходят к выводу: отношение длины окружности к ее диаметру соответствующей окружности есть число постоянное.
Одной из технологий системно-деятельностного подхода, которую мы применяем, является метод проектов, который мы рассматриваем как специальную форму организации познавательной деятельности.
Метод проектов позволяет строить учебный процесс, исходя из интересов обучающихся, дает возможность обучающемуся проявить самостоятельность в планировании, организации и контроле своей учебно-познавательной деятельности. Метод проектов ориентирован на самостоятельную деятельность обучающихся – индивидуальную, парную, групповую, реализующуюся в течение определенного отрезка времени. При выполнении проекта дети решают поставленную проблему, учатся применять знания из различных областей науки, техники. Результаты выполненных проектов являются «осязаемыми»: если это теоретическая проблема, то ее итогом является конкретное решение, если практическая – конкретный результат, готовый к использованию (на уроке, в школе и т.д.). Примерами краткосрочных проектов, реализуемых на одном уроке, могут служить «Ремонт комнаты» (при изучении темы «Площади и объемы» в 5 классе); «Бизнес-план строительства катка» (по теме «Основные задачи на дроби» в 6 классе), «Экскурсионные маршруты по культурным местам Орехова-Зуева» (при изучении темы «Масштаб»).
При применении системно-деятельностного подхода учащиеся ставятся в такие условия, когда сами добывают знания, участвуют в учебных проектах; ставят личные цели для достижения определённого результата.
О каких-либо серьёзных результатах говорить ещё рано, но думаем, что можем говорить о таких метапредметных результатах как понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем; умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
Знать - значит не просто помнить определенные знания, а выполнять определенную деятельность, связанную с этими знаниями.







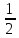 часть Карлсону, а
часть Карлсону, а 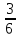 - всем остальным. Как вы считаете, все ли получат поровну?
- всем остальным. Как вы считаете, все ли получат поровну?









