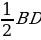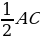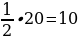Россия, Верхняя Пышма, Свердловская область
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 22.06.2025 15:00
Ячменева Алена Сергеевна
учитель математики
1 141
53 296 
Местоположение
Специализация
Параллелограмм (теория + разбор некоторых задач)
Категория:
Геометрия
31.10.2024 19:27
Просмотр содержимого документа
«Параллелограмм (теория + разбор некоторых задач)»
Параллелограмм
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны и равны.
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства параллелограмма
1. Противолежащие стороны равны.
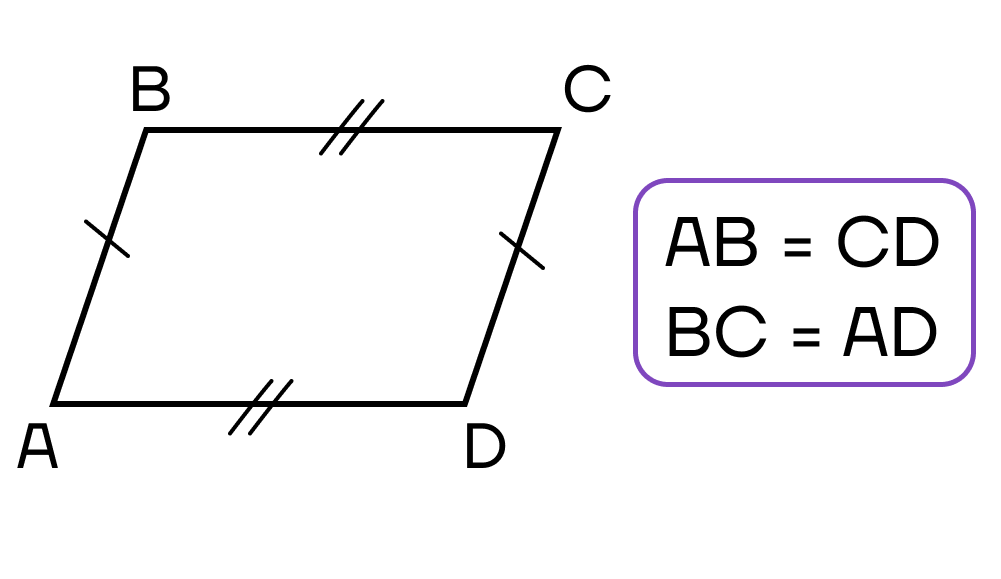
2. Противолежащие стороны параллельны.
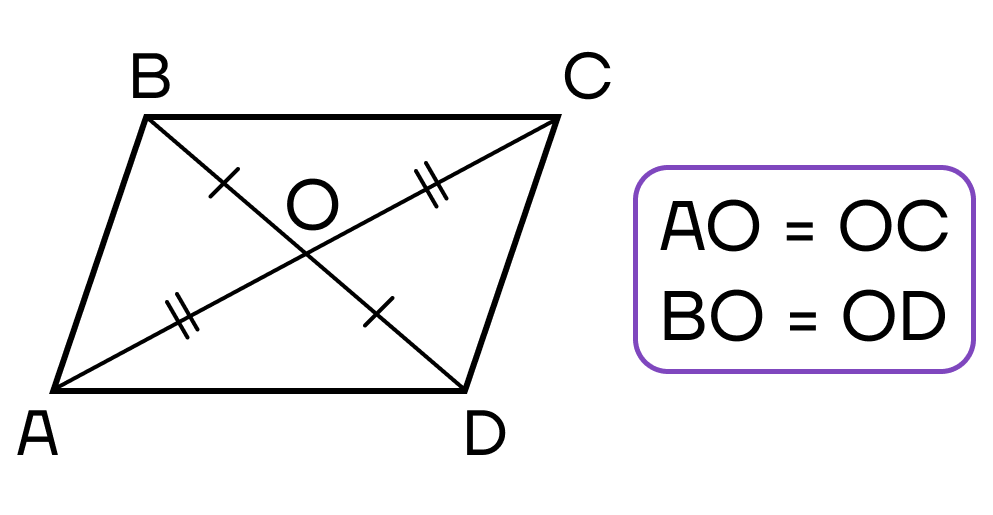
3. Диагонали пересекаются и точкой пересечения делятся пополам.
4. Сумма углов прилежащих к любой стороне равна 1800.
Т
.к. стороны AD и BC — параллельные прямые, а AB — секущая. Следовательно, по свойству двух параллельных прямых и секущей, это односторонние углы и их сумма равна 1800.
5. Противолежащие углы попарно равны. Доказывается через третий признак равенства треугольников, ∆ABD = ∆BDC все стороны равны, а значит и углы тоже.
Три основных признака:
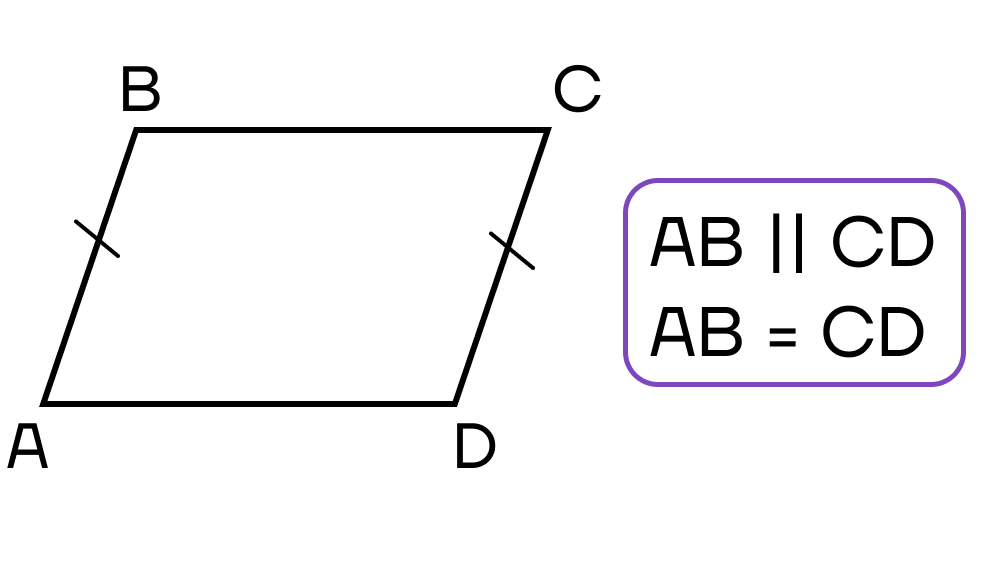
1. Две противоположные стороны четырехугольника параллельны и равны.
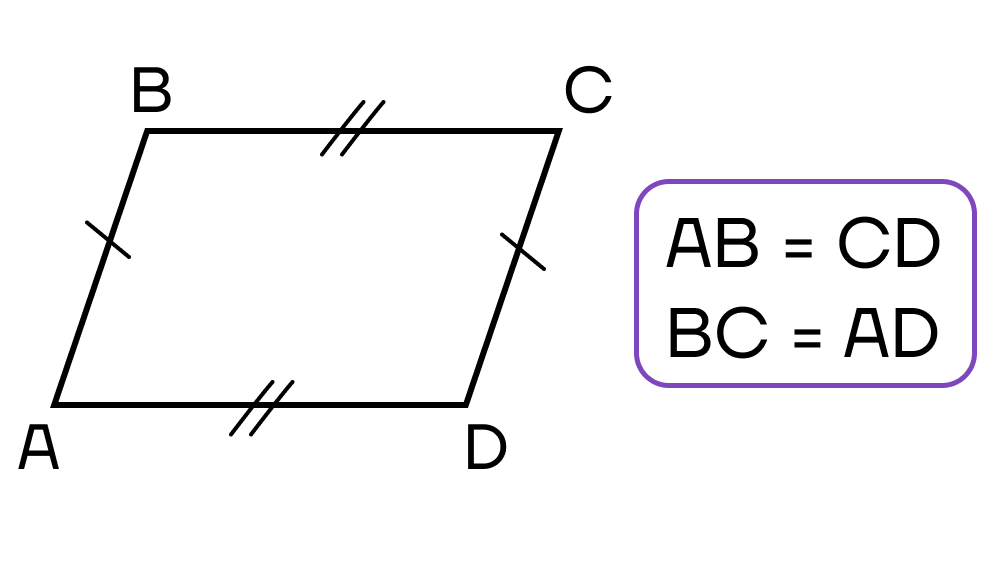
2. Противоположные стороны четырехугольника попарно равны.
3. Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.
Биссектриса в параллелограмме.
Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.
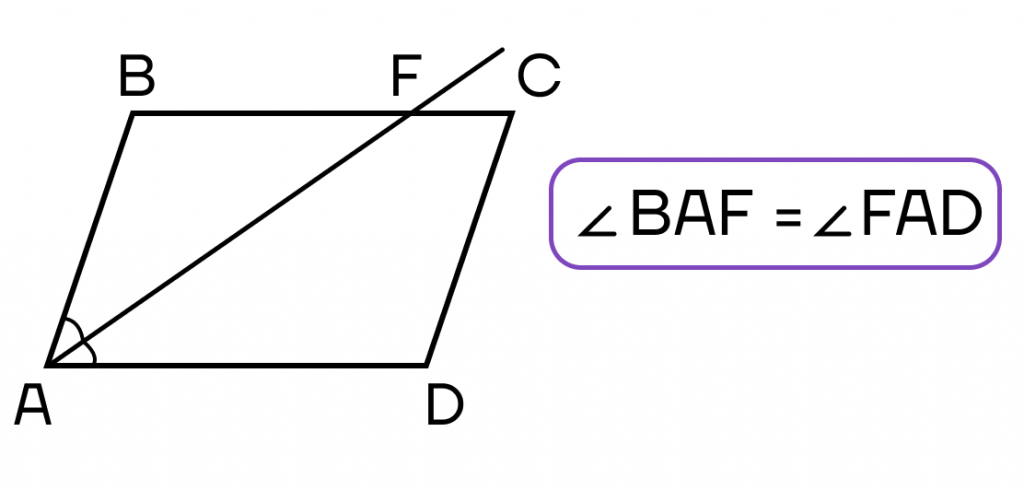
Два полезных факта, связанных с биссектрисой в параллелограмме.
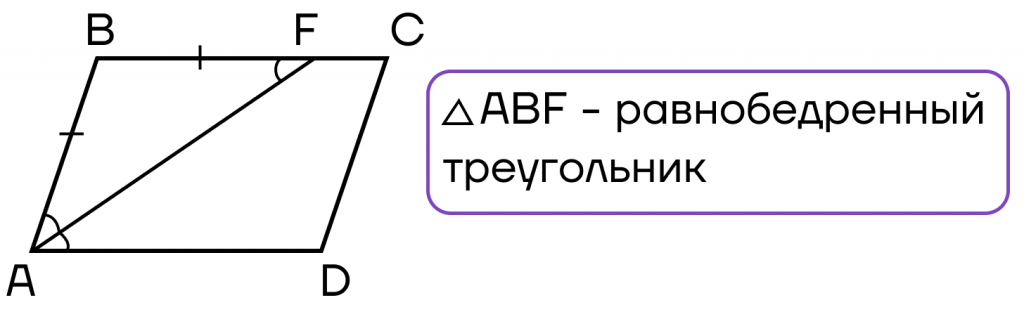
1. Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.
Доказывается с помощью параллельных прямых.
Рассмотрим две параллельные прямые: AD || BC – AF секущая.
∠FAD и= ∠BFA (накрест лежащие).
AF — биссектриса, то ∠BAF = ∠FAD, ∠FAD = ∠BFA тоже, значит и ∠BAF = ∠BFA. Следовательно, ∆BAF — равнобедренный.
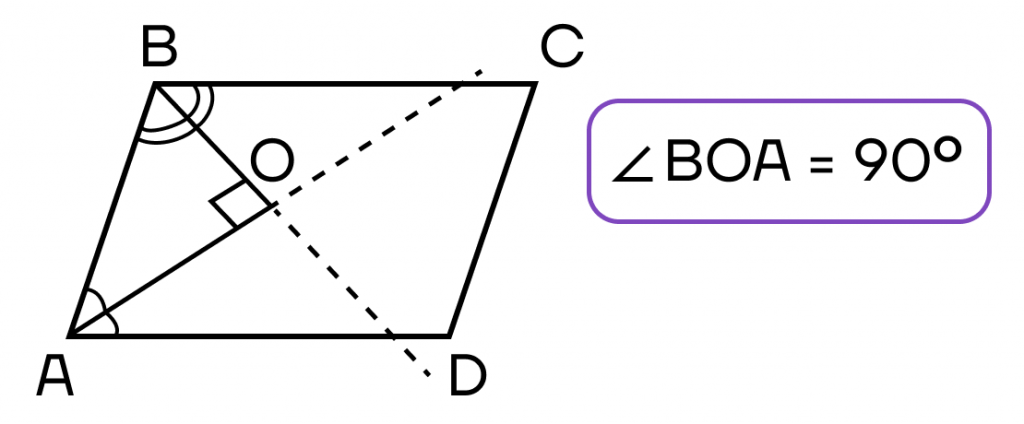
2. Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
Задание ОГЭ 17 вопрос
1. Один угол параллелограмма больше другого на 700. Найдите больший угол параллелограмма. Ответ дайте в градусах.
|
| Дано: АВСD – параллелограмм ∠В на 700 ∠A Найти: ∠В - ?
Решение: Обозначим ∠А = х, тогда ∠В = х+700 В параллелограмме сумма двух углов принадлежащие одной сторона 1800. х + х + 700 = 1800 2х=1800 – 700 2х=1100 х = 550 угол А ∠В = 550 + 700 = 1250 Ответ: 1250 |
2. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
|
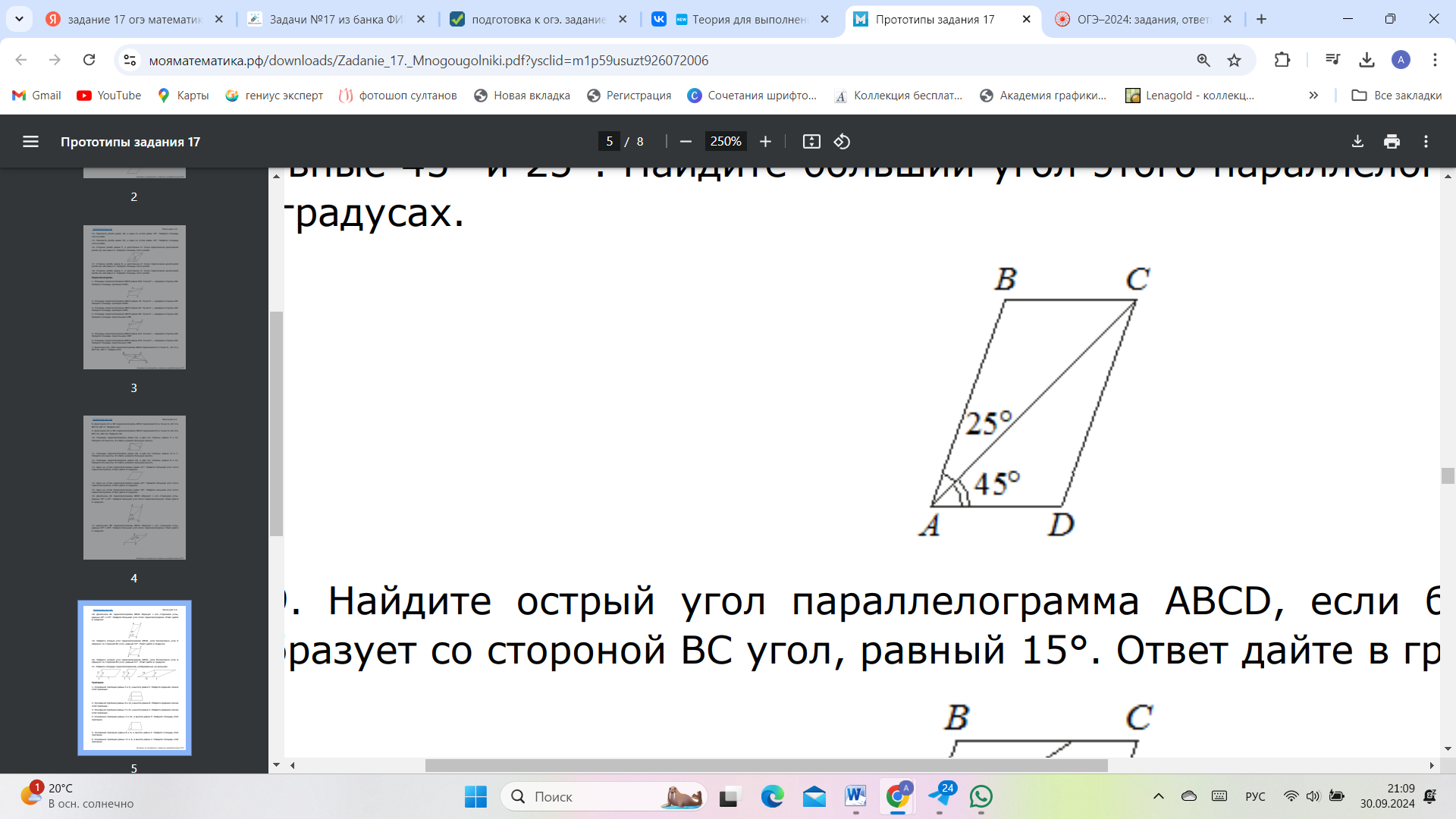
| Дано: АВСD – параллелограмм ∠ВАС = 250 ∠САD = 450 Найти: больший угол Решение: ∠А=∠ВАС + ∠САD ∠А = 250 + 450 = 700 ∠А = ∠С = 700 Сумма углов параллелограмма равна 3600. ∠В = ∠D = (3600 - 2∠А) : 2 ∠В = (3600 – 2 · 700) : 2 = 1100 Ответ: больший угол 1100 |
3. Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
|
К  | Дано: АВСD – параллелограмм АК – биссектриса ∠А ∠ВАК = ∠КАD ∠ВКА = 150 Найти: острый угол параллелограмма Решение: Рассмотрим ∆АВК ∠ВКА = ∠КАD (по условию) ∠КАD = ∠ВКА (накрест лежащие при ВС || АD и секущей АК) ∆АВК – равнобедренный ∠ВКА =∠ВАК = 150 ∠В = 1800 - 2∠ВАК = 1800 - 2· 15 = 1500 Ответ: больший угол 1500 |
4. Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 12, BD = 20, AB = 7. Найдите DO.
|
| Дана: АВСD – параллелограмм АС и ВD - диагонали АС ∩ ВD = O АС = 12 ВD = 20 АВ = 7 Найти: DO - ? Решение: В параллелограмме точки пересечения делятся пополам. ВO = OD = 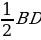АО = ОС = 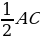DО = 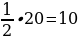Ответ: DО = 10 |
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
