Построение графика квадратичной функции 9 кл.Презентация

Ордашов Магомед Омарович,

МКОУ Гамияхская школа №2,

учитель математики

Конспект урока по алгебре.

Тема урока: Построение квадратичной функции.

Класс: 9

УМК: Учебник для 9 класса общеобразовательных учреждений.

Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковского. , 2011

Место урока: урок проводится после изучения построения функций у=ах²; у=ах²+n; у=а(х-m)²

Цели урока:

Образовательные:

1. Рассмотреть алгоритм построения графика квадратичной функции;

2. Способствовать развитию навыка построения квадратичной функции;

3. Формировать умение работать по алгоритму (образцу)

Развивающие:

1. Развитие аккуратности при построении чертежей, внимательности.

2. Формирования умения работать с ЦОР, программой Master Craph.

3. Формирование умения работать в парах, навыка самоконтроля.

Коррекционные:

1. Развитие у учащихся графических навыков;

1. Развитие зрительного внимания;

2. Развитие логического мышления

Место проведения урока: компьютерный класс.

Оборудование: - Персональные компьютеры, с установленной программой Stratum, для использования ЦОР .

- Программа Master Craph

- Мультимедийный проектор

- Презентация урока

- Распечатки с заданиями для учащихся

- таблицы с терминами : «вершина параболы»,

«ось симметрии»,

«функция»,

«нули функции»,

«парабола»

«корни квадратного трехчлена»

Ход урока.

I. Организационный момент

Приветствие учащихся. Вступительная беседа учителя. Просмотр слайдов №1—8.

Вопросы к демонстрации слайдов:

-Как вы думаете, по какому принципу объединены данные фотографии?

Ответы: контур всех объектов, изображенных на фотографиях, представляет собой параболу.

II. Актуализация знаний

Устная работа по пройденному материалу.

Из перечисленных формул, которые появились на доске, построение графика какой функции мы ещё не рассматривали?

y=ax² +bx+c.

Сегодня наша задача определить алгоритм построения графика квадратичной функции, заданной общей формулой. СЛАЙД №12

Тема сегодняшнего урока: Построение графика квадратичной функции.

Вопросы к учащимся.

Какие понятия, связанные с квадратичной функцией мы разбирали на предыдущих уроках? И что могли определить по графику или с помощью вычислений? СЛАЙД №13

Ответы: Вершина параболы, ось симметрии, нули функции

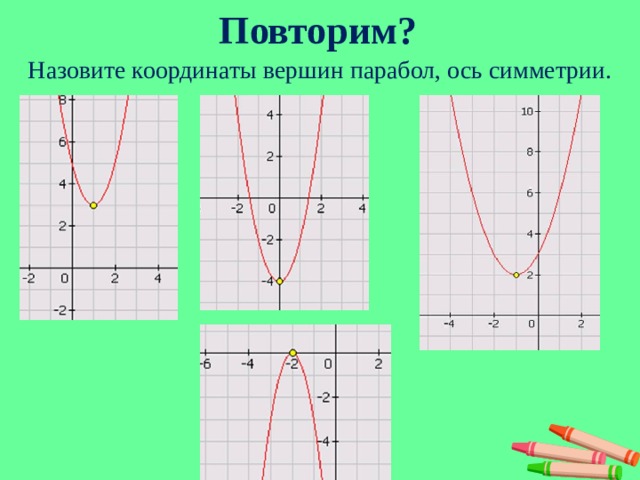
Эти понятия могут нам помочь и сегодня. Давайте их повторим. СЛАЙД №14

Перед вами лежат таблицы, в которых необходимо заполнить пустые графы.

Первая строка выполняется учащимися у доски под контролем учителя. Далее выполнение работы в парах.

Работа по таблице, с использованием образца выполнения.

СЛАЙД №15

Задание №1. заполните пустые графы, найдя вершину параболы, нули функции.

Проверка заполненной таблицы. СЛАЙД №16

Устные выступления от каждой пары, с комментариями по выполнению задания.

Обобщение выполненной работы:

• повторение формулы для нахождения вершины параболы,

• алгоритма нахождения нулей функции и их геометрический смысл.

Вопросы к учащимся: формулы, какой функции представлены в таблице, от чего зависит направления ветвей параболы. Как вы думаете, сможем ли мы, используя полученные данные, построить графики представленных функций? Что для этого надо сделать?

Ответы: построить точки и соединить линией.

Вопрос: Что должно получиться в итоге построения?- парабола.

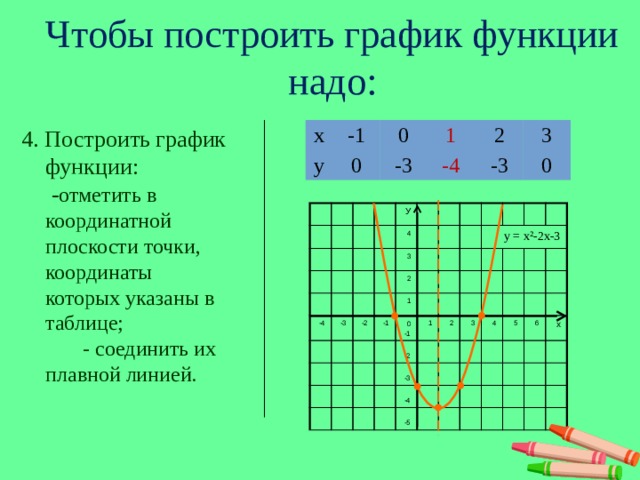
Задание №2. Отметить на координатной плоскости полученные точки.

Для этого у каждого учащегося лежат 4 листа миллиметровки, с заранее построенными координатными плоскостями.

Лист №1. Отметим координаты вершины параболы и нули функции №1. Соединим точки плавной линией.

Лист №2. Отметим координаты вершины параболы и нули функции №2. Соединим точки плавной линией.

Аналогично выполняем на листах №3, 4,

Что в итоге мы с вами получили? – В каждом случае построена параболу.

Задание №3. Проверим, правильно ли мы с вами построили график? И сделаем это с помощью программы Master Craph, установленной на ваших компьютерах. Войдите в программу, выполняя последовательно все указанные действия.

СЛАЙД №17

Слайд №18

Обобщение выполненного задания: Для построения графика квадратичной функции мы использовали вершину параболы, нули функции.

III. Новый материал.

- график какой функции вызвал затруднение при построении? Почему?

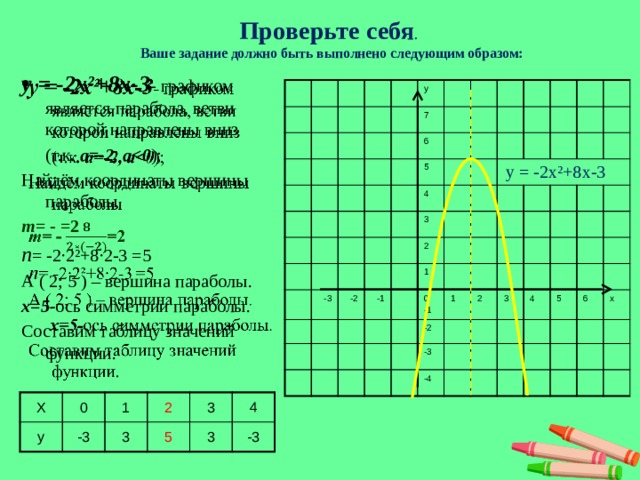
- Какое из перечисленных условий не всегда может быть точно найдено? Для этого рассмотрим построение графика функции у= -2х²- 8х- 5.

- Заполните уже знакомую нам таблицу и построим полученные точки на координатной плоскости.

Проблема: не построить точно нули функции.

Что может помочь нам? Дополнительные точки. Ось симметрии.

Построение таблицы значений функции, с учетом симметричных точек.

Проверяем с помощью программы Master Craph.

Вопросы к учащимся по ходу выполнения задания: Надо ли всегда находить нули функции? В каком случае график будет более точным?

Показ СЛАЙДА раздел «Усвоение знаний и навыков по теме «Построение квадратичной функции» Теория. «Алгоритм построения квадратичной функции» с помощью ЦОР к учебнику «Алгебра», 9 класс, Ю.Н. Макарычев, Миндюк Н.Г. и др.

http://school-collection.edu.ru/catalog/rubr/73bc8240-49f3-44c6-8991-a547d457a20f/112754/?interface=catalog&class=51&subject=17

Работа по учебнику. Алгоритм построения графика квадратичной функции стр.41.

IV. Первичное закрепление материала.

Рассмотрение построение графика функции у= х²- 4х- 2. Поэтапное построение на слайде №21

Работа в тетрадях.

Совместное выполнение задания № 121. Проверка с помощью программы Master Craph.

V. Проверка качества усвоения материала.

Выполнение самостоятельной работы.

Построить графики функций у= х²- 2х+ 8

у= -х²- 4х+ 2

Самопроверка с помощью программы Master Craph .

VI. Подведение итогов урока.

VII. Инструктаж по выполнению домашнего задания.

Алгоритм построения графика квадратичной функции стр.41,

№125(в), 126(б).

№131

Повторим?

Назовите координаты вершин парабол, ось симметрии.

Установите соответствие между графиком функции

формулой и координатами вершины параболы:

9

У

У

У

9

9

4

1

4

4

Х

1

3

2

-1

1

1

Х

Х

3

2

1

2

3

1

-1

-1

Установите соответствие между графиком функции,

формулой и координатами вершины параболы:

9

У

У

У

9

9

4

1

4

4

Х

3

1

2

-1

1

1

Х

Х

3

3

2

1

1

2

-1

-1

Опираясь на ранее изученный материал определить, по какому признаку можно объединить следующие рисунки

Падение баскетбольного мяча

3

Параболический фонтан

3

Библиотека с крышей в форме параболы в Норвегии

3

Лучи прожектора

3

Параболическая солнечная электростанция в Калифорнии (США)

3

Вращающийся сосуд с жидкостью

3

ТЕМА УРОКА:

Построение графика

квадратичной функции

Цели урока:

• Сформулировать алгоритм построения графика квадратичной функции, т. е. функции вида y = ax 2 +bx+c.
• Выработать умение строить график квадратичной функции по алгоритму.

3

Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c , где x - независимая переменная, a, b и с -некоторые числа (причём а≠0 ).

Например:

• у = 5х²+6х+3,
• у = -7х²+8х-2,
• у = 0,8х²+5,
• у = ¾ х²-8х,
• у = -12х²

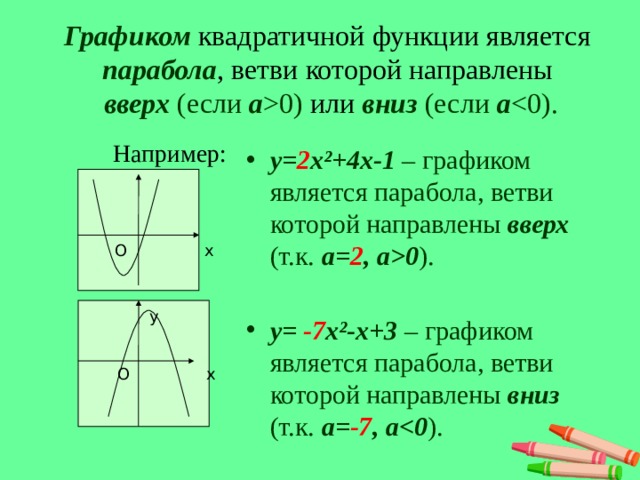0) или вниз (если а Например: у= 2 х²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а= 2 , а0 ). у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а= -7 , а ). О х у О х" width="640"

Графиком квадратичной функции является парабола , ветви которой направлены вверх (если а 0) или вниз (если а

Например:

• у= 2 х²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а= 2 , а0 ).

• у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а= -7 , а ).

О х

у

О х

Чтобы построить график функции надо

1. Описать функцию:

Пример: у = х²-2х-3

• что является графиком функции
• куда направлены ветви параболы

• графиком является парабола,
• ветви которой направлены вверх (т.к. а=1, а0 )

Чтобы построить график функции надо

•  

2. Найти координаты вершины параболы А(m;n) по формулам:

m = -

n = у( m )

т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.

Прямая x=m является осью симметрии параболы.

Пример: y=x 2 -2x-3

•  

(a=1, b=-2, c=-3)

Найдём координаты вершины параболы:

m =-=1;

n =1 2 -2-3=-4

A(1;-4)- вершина параболы

x=1-ось симметрии параблы

Чтобы построить график функции надо

3. Заполнить таблицу значений функции:

• прямая x=m ось симметрии
• вершину параболы расположить в середине таблицы
• посчитать значение функции в выбранных значениях х

Пример : у = х²-2х-3

А(1;- 4) – вершина параболы

х=1 – ось симметрии параболы.

Составим таблицу значений функции:

х

х

у

у

m-2

- 1

m-1

0

0

1

m

- 3

- 4

n

2

m+1

- 3

3

m+2

0

Чтобы построить график функции надо:

4. Построить график функции: - отметить в координатной плоскости точки, координаты которых указаны в таблице; - соединить их плавной линией.

х

-1

у

0

0

1

-3

-4

2

-3

3

0

У

4

-4

3

-3

2

-2

1

-1

у = х²-2х-3

0

-2

1

-1

-3

2

-4

3

-5

4

5

6

х

Постройте график функции у = -2х²+8х-3 План построения :

1. Описать функцию:

•  

• что является графиком функции; куда направлены ветви параболы
• что является графиком функции;
• куда направлены ветви параболы

2. Найти координаты вершины параболы А( m;n)

по формулам: m = - n = у(m)

3. Заполнить таблицу значений функции.

4. Построить график функции:

• отметить в координатной плоскости точки, координаты которых указаны в таблице; соединить их плавной линией.
• отметить в координатной плоскости точки, координаты которых указаны в таблице;
• соединить их плавной линией.

Проверьте себя . Ваше задание должно быть выполнено следующим образом:

у = -2х²+8х-3 - графиком является парабола, ветви которой направлены вниз

•  

(т.к . а=-2, а );

Найдём координаты вершины параболы

m = - =2

n = -2·2²+8·2-3 =5

А ( 2; 5 ) – вершина параболы.

х=5- ось симметрии параболы.

Составим таблицу значений функции.

у

7

6

5

-3

4

-2

3

2

-1

у = -2х²+8х-3

1

0

-2

1

-1

-3

2

-4

3

4

5

6

х

Х

у

0

1

-3

2

3

5

3

3

4

-3

Если у вас получилось тоже самое – вы молодец и я вас поздравляю!!!

Перед продолжением работы запишите домашнее задание

Д/З

Запишите домашнее задание:

П.2.4; №265(а,в),№ 268(а,в),№270.

Желаем успехов!

Выполните следующую работу в тетрадях по вариантам. Постройте графики функций:

• II вариант

у = -х²-6х-7

• I вариант

у = -х²+6х-8

Желаем успеха!

Оцените своё настроение и состояние после проведённого урока.

Спасибо за внимание!

Список литературы:

• Дорофеев Г.В. Алгебра 9 класс .Учебник. М.:Просвещение, 2011г.
• Минаева С.С. Алгебра .Рабочая тетрадь.Просвещение ,2011г.