Презентация к уроку математика в 9 классе по теме "Площадь.Задачи ОГЭ"

Модуль «Геометрия»

Задание № 17 Площади фигур

«Знания по геометрии или умение пользоваться формулами необходимы почти каждому мастеру или рабочему»

А.Н. Колмогоров

Выполнила Трофимова Т.Н.

МОУ «СОШ №58»

Цель нашего урока обобщить, систематизировать, проверить и оценить ваши знания по теме «Площади геометрических фигур»!!!!

ВЕРНО ИЛИ НЕВЕРНО ?

• Площадь трапеции равна половине высоты, умноженной на разность оснований.
• Существует прямоугольник, диагонали которого взаимно перпендикулярны
• В любой четырехугольник можно вписать окружность.
• Отношение площадей подобных треугольников равно коэффициенту подобия.
• Площадь параллелограмма равна половине произведения его диагоналей.
• Существует треугольник со сторонами 6,8,10.
• Две прямые, перпендикулярные третьей прямой, параллельны друг другу.
• Биссектрисы треугольника пересекаются в центре вписанной в него окружности

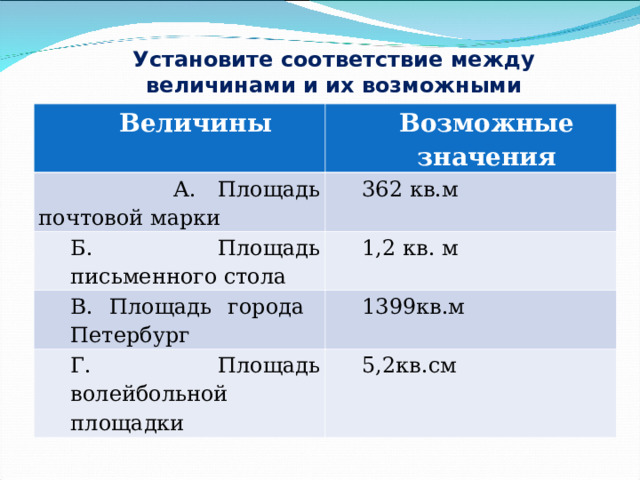
Установите соответствие между величинами и их возможными значениями

Величины

Возможные значения

А. Площадь почтовой марки

362 кв.м

Б. Площадь письменного стола

1,2 кв. м

В. Площадь города Петербург

1399кв.м

Г. Площадь волейбольной площадки

5,2кв.см

Найдите соответствующую формулу

• .
• .
• .
• .
• .
• .
• .
• .
• .
• .
• .
• .

• Площадь прямоугольного

треугольника с катетами a , b

• Площадь треугольника, если известен угол между сторонами
• Площадь круга
• Площадь трапеции
• Площадь параллелограмма, если известна высота
• Площадь параллелограмма, если известен угол между смежными сторонами
• Длина окружности
• Средняя линия треугольника
• Средняя линия трапеции
• Теорема Пифагора
• Теорема косинусов
• Теорема синусов
• Длина дуги окружности

Решение задач из

ОТКРЫТОГО БАНКА ОГЭ

Найдите площадь параллелограмма, изображённого на рисунке.

Решение:

S = a*h

S = (3+7)*4= 40

Ответ: 40

Решение задач из ОТКРЫТОГО БАНКА ОГЭ

Найдите площадь параллелограмма, стороны которого равны 2√3 и 5, а один из углов равен 1200.

Решение:  

S = ab sinα,        

S= 2√3 * 5 *√3/2 = 15,    

Ответ: 15.

Решение задач из ОТКРЫТОГО БАНКА ОГЭ

  Площадь прямоугольного треугольника равна 96, а один из катетов равен 16. Найдите гипотенузу данного треугольника.

Решение:  

S = ½ ab,    

  b = 2S/a,    

  b = 2 *96/16 = 12,    

  с = √256 + 144 = 20      

Ответ: 20.

Решение задач из ОТКРЫТОГО БАНКА ОГЭ

Найдите площадь квадрата, описанного около окружности радиуса 40.

Решение:

S = a^2

S = 80^2= 6400

Решение задач из ОТКРЫТОГО БАНКА ОГЭ

Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.

Решение:

S = ½(a + b)*h

S= ½ (5+13)*9 = 81

Ответ: 81

Самостоятельная работа

Вариант 2

Вариант 1

1. Площадь прямоугольника 20см ^ 2, одна из сторон – 5см. Найти другую сторону.

   1) 15см            2) 4см             3) 5см         4) 100см

2. В параллелограмме одна из сторон 7см, высота, опущенная на нее 3см. Найти площадь.     

   1) 21см   2) 10см ^ 2      3) 21см ^ 2         4)10,5см ^ 2

3. В треугольнике высота, опущенная к стороне с длиной 10см,  равна 6см. Найти площадь.   

     1) 60см ^ 2        2)30см ^ 2    3)16см ^ 2     4) 8см ^ 2

4. Радиус круга 3дм. Найти площадь.

     1) 3π дм ^ 2   2) 9 дм ^ 2  3) 9π дм ^ 2   4) 9π ^ 2 дм ^ 2

5. Площадь квадрата 4 м ^ 2. Найти периметр квадрата.        

1) 1 м             2) 8 м                3) 2 м                4) 16 м

1. Площадь прямоугольника 40см ^ 2, одна из сторон –10см. Найти другую сторону.     

   1) 4см        2) 2см            3) 30см                4) 200см

2. В параллелограмме одна из сторон 8см, высота, опущенная на нее 5см. Найти площадь.

         1) 13см      2) 40см ^ 2      3) 40см       4) 26см ^ 2

3. В треугольнике высота, опущенная к стороне с длиной 9см, равна 4см. Найти площадь.

         1) 35см ^ 2     2) 13см ^ 2    3) 18см ^ 2   4) 72см ^ 2

4. Радиус круга 4дм. Найти площадь.

      1) 16π дм ^ 2    2) 4π дм ^ 2 3) 16 ^ 2 дм ^ 2  4) 16 дм ^ 2

5. Площадь квадрата 16 м. Найти периметр квадрата.

   1) 4 м       2) 64 м             3) 8 м              4) 16 м

Отметка: «5» - нет ошибок, «4» - 1 ошибка, «3» - 2 ошибки, более двух неверных ответов – выучи формулу, упражняйся в устном счете.

Вариант 1

Вариант 2

1 - 1

2 - 2

3 - 3

4 - 1

5 - 4

1 - 2

2 - 3

3 - 2

4 - 3

5 - 2