Презентация " Статистическая обработка данных" алгебра 11 класс

Статистическая обработка данных

Алгебра – 11 класс

На праздничном вечере среди учеников провели лотерею. Каждый из 50 школьников произвольно задумал одну цифру от0 и до 9 и записал ее на левой и правой половинках своего билета. Правые половинки остались у их владельцев а левые попали на стол к организаторам лотереи. Итак, на столе 50 листочков, содержащих необходимую информацию. Как в ней разобраться?

Решение:

Первое, надо как-то упорядочить и сгруппировать данные.Результат группировки показан в таблице.

После этого всем участникам раздавали небольшие призы по шуточным номинациям:

• «Самый популярный» (ответ 5)
• «Почти самый популярный» (ответ 3)
• «Оригинально, но неверно» (ответ 10)
• «Сладкая парочка» (ответ 0)
• «Три богатыря» (ответ 2,6,8)
• «Отличники» (ответы 1,7,9)
• «Хорошисты» (ответ 4).

Ответ

0

Количество ответов

2

1

2

5

3

3

9

4

4

5

6

10

3

7

8

5

3

9

10

5

1

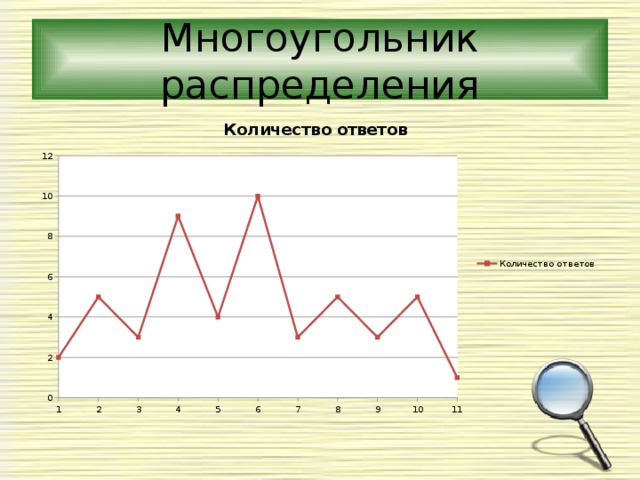
Многоугольник распределения

Гистограмма распределения

Основные этапы простейшей статистической обработки данных:

• Данные упорядочивают и группируют.
• Составляют таблицы распределения данных.
• Строят графики распределения данных (гистограмма, круговая диаграмма).

• Получения паспорта данных измерения (числовые характеристики).

Числовые характеристики

• Объем измерения (50 участников).
• Размах измерения (разность между наибольшим и наименьшим результатами 10-0=10)
• Мода измерения (значение, встречающееся чаще всего – 5)
• Среднее или среднее арифметическое (частное от деления суммы всех результатов измерения на объем измерения – 4.72)

Варианта измерения – каждое число, встретившееся в конкретном измерении.

Если записать все варианты измерения по порядку их получения, то получим ряд данных измерения. Если начать с наименьшей из вариант измерения и записать все остальные в порядке возрастания, то получим сгруппированный ряд данных.

0,0, 1,…1, 2,2,2, 3,…3, 4,4,4,4, 5,…5, 6,6,6, 7,…7, 8,8,8, 9,…9, 10.

2 5 3 9 4 10 3 5 3 5 1

Среднюю варианту в сгруппированном ряде называют медианой измерения. Если таковых две, то медиана равна их полусумме ( в нашем примере №25 – 5 и № 26- 5, значит медиана – 5).

Определение: Если среди всех данных конкретного измерения одна из вариант встретилась k раз, то число k называют кратностью (абсолютной частотой) этой варианты.

Так получается таблица распределения данных измерения.

Варианта

Кратность

0

2

1

5

2

3

3

9

4

5

4

6

10

7

3

5

8

3

9

10

Сумма

5

1

50

Решение задач

№ 1.

На уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их результаты. Получился такой ряд данных (в сантиметрах):

125, 110, 130, 125, 120, 130, 140, 125, 110, 130, 120, 125, 120, 125.

Требуется сгруппировать данные, составить таблицу их распределения, найти размах, моду и медиану измерения.

РЕШЕНИЕ:

Выпишем все варианты измерения в порядке возрастания:

110, 110, 120, 120, 120, 125, 125, 125, 125, 125, 130, 130, 130, 140.

Размах измерения равен 140-110=30. Варианта 125 встретилась наибольшее число раз и ее кратность равна 5; это мода измерения.

Составим таблицу распределения данных:

125 – медиана измерения.

№ 2.

В таблице распределения часть данных утеряна. Восстановите ее, если известно, что объем измерения равен 20, размах равен 6, а мода равна 2.

Варианта

Кратность

110

2

120

125

3

130

5

140

Сумма

3

1

14

Варианта

Кратность

-1

5

0

1

Сумма

3

7

3

- 3

2

4

20

По определению, в графе «Сумма» должен стоять объем измерения, он равен 20. Кратность варианты «0» равна 20 – (5+1+7+3)= 4.

Самая большая кратность равна 7. Значит, над ней и располагается мода измерения, равна 2. Так как размах равен 6, а наибольшая варианта равна 3, то наименьшая варианта равна 3-6 = -3. Эту варианту помещаем в пустую ячейку над кратностью 5.