Продолжение лекции 9 (10) Формулы Ньютона - Котеса: методы прямоугольников, трапеций, парабол
Цель: повторить теоретические знания, полученные в лекции 9, закрепить теорию выполнением практической части
ОТЧЁТ ПРЕДОСТАВИТЬ В ВИДЕ ДОКУМЕНТА EXCEL. В НАЗВАНИИ УКАЗАВ ФАМИЛИЮ НОМЕР ГРУППЫ
Вычисление определенных интегралов вида

Постановка задачи
Пусть требуется вычислить определенный интеграл  , где f(x) – непрерывная на отрезке [a; b] функция.
, где f(x) – непрерывная на отрезке [a; b] функция.
Вычислить определенный интеграл можно с помощью аналитической формулы:
 – формула Ньютона-Лейбница.
– формула Ньютона-Лейбница.
Однако во многих случаях не удается преобразовать f(x) к табличной функции, для которой известна аналитическая формула F(x). В таких случаях приходится решать задачу численного интегрирования.
Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитическом виде, некоторой простой табличной функцией φ(x). Поскольку в этом случае решение является приближенным, то в постановке задачи необходимо задавать точность .
Обзор методов численного интегрирования
Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными).
К квадратурным методам относятся методы Ньютона-Котеса. В этих методах φ(x) – это полиномы различных степеней, к ним относятся: метод прямоугольников, метод трапеций, метод Симпсона.
Метод прямоугольников
Постановка задачи
Дан определенный интеграл  , где f(x)– функция непрерывная на отрезке [a; b] и точность – малое положительное число. Необходимо вычислить интеграл с заданной точностью.
, где f(x)– функция непрерывная на отрезке [a; b] и точность – малое положительное число. Необходимо вычислить интеграл с заданной точностью.
Графическая интерпретация метода
С геометрической точки зрения интеграл при f(x) 0 равен площади криволинейной трапеции, ограниченной кривой y = f(x), осью Ox и прямыми x = a, x = b. Разобьем отрезок [a; b] на n равных частей: x0=a, x1=x0+h, x2=x1+h, … , xn=b, где h=(b-a)/n. Площадь всей криволинейной трапеции заменим суммой площадей «маленьких» криволинейных трапеций, образованных при проведении прямых x=xi. Заменим при вычислении площади каждую «маленькую» криволинейную трапецию прямоугольником, то есть заменим кривую f(x) полиномом нулевой степени – отрезком, параллельным оси абсцисс. При этом прямоугольники можно построить тремя разными способами, взяв за одну из сторон прямоугольника ординату xi-1, или xi, или (xi-1+xi)/2. Таким образом, различают методы левых, правых и средних прямоугольников.

Алгоритм метода прямоугольников
Вводим исходные значения , a, b.
Задаем n=1, S=0.
Приравниваем S0=S, .n=2·n.
Расчет h=(b-a)/n.
Расчет приближенного значения интеграла:
Метод прямоугольников с недостатком (левые прямоугольники).
Приближенное значение интеграла равно сумме площадей прямоугольников:

Метод прямоугольников с избытком (правые прямоугольники).
Приближенное значение интеграла равно сумме площадей прямоугольников:

Метод средних прямоугольников.
Приближенное значение интеграла равно сумме площадей прямоугольников:

Проверка условия |S0-S| ε. Если условие выполняется, то переход к пункту 7, иначе переход к пункту 3.
Расчет закончен. Результат равен S.
Реализация метода в MS Excel
Вычислить  dx с точностью =0,001.
dx с точностью =0,001.
Заполнение клеток листа MS Excel для n=2:
| Адрес клетки | Содержание | Тип |
| A1 | n=2 | Текст |
| C1 | a= | Текст |
| D1 | 0 | Число |
| E1 | b= | Текст |
| F1 | 0,5 | Число |
| B2 | h= | Текст |
| C2 | =(F1-D1)/2 | Формула |
| A4 | x | Текст |
| B4 | xcp | Текст |
| C4 | f левые прямоугольники | Текст |
| D4 | f правые прямоугольники | Текст |
| E4 | f средние прямоугольники | Текст |
| A5 | =D1 | Формула |
| B5 | =(A5+A6)/2 | Формула |
| C5 | =EXP(-A5*A5/2) | Формула |
| D5 | =EXP(-A6*A6/2) | Формула |
| E5 | =EXP(-B5*B5/2) | Формула |
| A6 | =A5+$C$2 | Формула |
| B6 | =(A6+A7)/2 | Формула |
| C6 | =EXP(-A6*A6/2) | Формула |
| D6 | =EXP(-A7*A7/2) | Формула |
| E6 | =EXP(-B6*B6/2) | Формула |
| B6 | Результат | Текст |
| C6 | =СУММ(C5:C6)*$C$2 | Формула |
| D6 | =СУММ(D5:D6)*$C$2 | Формула |
| E6 | =СУММ(E5:E6)*$C$2 | Формула |
Вид листа MS Excel:

Результаты расчета для n=2:
по методу левых прямоугольников 0,4923;
по методу правых прямоугольников 0,4629;
по методу средних прямоугольников 0,4811.
Заполнение клеток листа MS Excel для n=4:
| Адрес клетки | Содержание | Тип |
| H1 | n=4 | Текст |
| J1 | a= | Текст |
| K1 | 0 | Число |
| L1 | b= | Текст |
| M1 | 0,5 | Число |
| I2 | h= | Текст |
| J2 | =(M1-K1)/4 | Формула |
| H4 | x | Текст |
| I4 | xcp | Текст |
| J4 | f левые прямоугольники | Текст |
| K4 | f правые прямоугольники | Текст |
| L4 | f средние прямоугольники | Текст |
| H5 | =K1 | Формула |
| I5 | =(H5+H6)/2 | Формула |
| J5 | =EXP(-H5*H5/2) | Формула |
| K5 | =EXP(-H6*H6/2) | Формула |
| L5 | =EXP(-I5*I5/2) | Формула |
| I6:L8 | автозаполнение формулами диапазона I5: L5 | Формула |
| H6 | =H5+$J$2 | Формула |
| H7:H8 | автозаполнение формулой из H6 | Формула |
| I10 | Результат | Формула |
| J5 | =СУММ(J5:J8)*$J$2 | Формула |
| K5 | =СУММ(K5:K8)*$J$2 | Формула |
| L5 | =СУММ(L5:L8)*$J$2 | Формула |
Вид листа MS Excel:

Результаты расчета для n=4:
по методу левых прямоугольников 0,4867;
по методу левых прямоугольников 0,4720;
по методу левых прямоугольников 0,4802.
Далее выполняем расчеты для n=8,16,32.
Вид листа MS Excel для n=8:
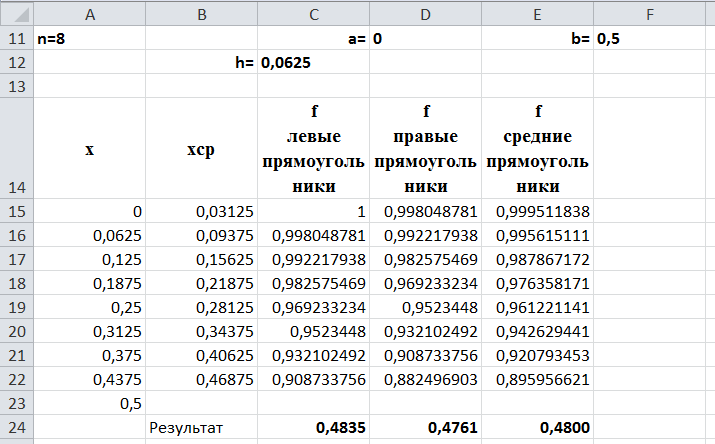
Результаты расчета для n=8:
по методу левых прямоугольников 0,4835;
по методу правых прямоугольников 0,4761;
по методу средних прямоугольников 0,4800.
Вид листа MS Excel для n=16:
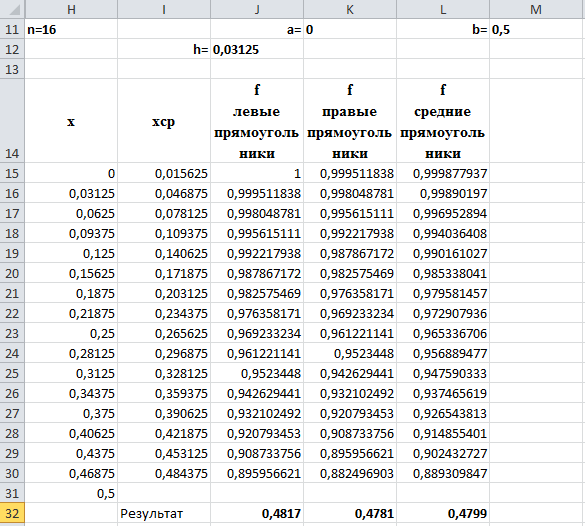
Результаты расчета для n=16:
по методу левых прямоугольников 0,4817;
по методу правых прямоугольников 0,4781;
по методу средних прямоугольников 0,4799.
Вид листа MS Excel для n=32:

Результаты расчета для n=32:
по методу левых прямоугольников 0,4808;
по методу правых прямоугольников 0,4790;
по методу средних прямоугольников 0,4799.
Вид таблицы результатов:

Проанализировав значения в этой таблице, увидим, что требуемая точность 0,001 достигнута на четвертой итерации для методов левые и правые прямоугольники и второй итерации для метода средние прямоугольники.
Метод трапеций
Графическая интерпретация метода
Разобьем отрезок [a; b] на n равных частей: x0=a, x1=x0+h, x2=x1+h, … , xn=b, где h=(b-a)/n. Площадь всей криволинейной трапеции заменим суммой площадей «маленьких» криволинейных трапеций, образованных при проведении прямых x=xi. Заменим при вычислении площади каждую «маленькую» криволинейную трапецию прямолинейной трапецией, то есть заменим кривую f(x) полиномом первой степени – отрезком прямой, соединяющей точки Mi-1{xi-1,f(xi-1)} и Mi{xi,f(xi)}.

Алгоритм метода трапеций
Вводим исходные значения , a, b.
Задаем n=1, S=0.
Приравниваем S0=S, .n=2·n.
Расчет h=(b-a)/n.
Расчет приближенного значения интеграла:

6. Проверка условия |S0-S| ε. Если условие выполняется, то переход к пункту 7, иначе переход к пункту 3.
7. Расчет закончен. Результат равен S.
Реализация метода в MS Excel
Вычислить  dx с точностью =0,001.
dx с точностью =0,001.
Заполнение клеток листа MS Excel для n=2:
| Адрес клетки | Содержание | Тип |
| A1 | n=2 | Текст |
| A2 | a= | Текст |
| B2 | 0 | Число |
| A3 | b= | Текст |
| B3 | 0,5 | Число |
| A4 | h= | Текст |
| B4 | =(B3-B2)/2 | Формула |
| A6 | x | Текст |
| B6 | f | Текст |
| A7 | =B2 | Формула |
| B7 | =EXP(-A7*A7/2) | Формула |
| A8 | =A7+$B$4 | Формула |
| B8 | =EXP(-A8*A8/2) | Формула |
| A9 | =A8+$B$4 | Формула |
| B9 | =EXP(-A9*A9/2) | Формула |
| A10 | S= | Текст |
| B10 | =B4*((B7+B9)/2+B8) | Формула |
Вид листа MS Excel:

Ответ: 0,4776.
Заполнение клеток листа MS Excel для n=4:
| Адрес клетки | Содержание | Тип |
| D1 | n=4 | Текст |
| D2 | a= | Текст |
| E2 | 0 | Число |
| D3 | b= | Текст |
| E3 | 0,5 | Число |
| D4 | h= | Текст |
| E4 | =(E3-E2)/4 | Формула |
| D6 | x | Текст |
| E6 | f | Текст |
| D7 | =E2 | Формула |
| E7 | =EXP(-D7*D7/2) | Формула |
| D8 | =D7+$E$4 | Формула |
| D9:D11 | Автозаполнение формулой из клетки D8 | Формула |
| E8:E11 | Автозаполнение формулой из клетки Е7 | Формула |
| D12 | S= | Текст |
| E12 | =E4*((E7+E11)/2+СУММ(E8:E10)) | Формула |
Вид листа MS Excel:

Ответ: 0,47935.
Далее выполняем расчеты для n=8,16.
В клетку H16 вводим формулу =H4*((H7+H15)/2+СУММ(H8:H14)).
Вид листа MS Excel для n=8:

Ответ: 0,479782.
В клетку К24 вводим формулу =K4*((K7+K23)/2+СУММ(K8:K22)).
Вид листа MS Excel для n=16:

Ответ: 0,479889.
Вид таблицы результатов:

Проанализировав значения в этой таблице, увидим, что требуемая точность 0,001 достигнута на второй итерации.
Метод Симпсона (метод парабол)
Графическая интерпретация метода
Разобьем отрезок [a; b] на n равных частей: x0=a, x1=x0+h, x2=x1+h, … , xn=b, где h=(b-a)/n. Площадь всей криволинейной трапеции заменим суммой площадей «маленьких» криволинейных трапеций, образованных при проведении прямых x=xi. Заменим при вычислении площади каждой «маленькой» криволинейной трапеции кривую f(x) полиномом второй степени – параболой. Для построения параболы требуется три точки, поэтому будем рассматривать не одну «маленькую» криволинейную трапецию, а две. Следовательно, чтобы каждая «маленькая» криволинейная трапеция, нашла пару необходимо, чтобы n было четным. Итак, подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла.

Возьмем три узла x0, x1, x2, через которые проведем параболу, воспользовавшись формулой Ньютона:

Пусть z = x - x0, тогда
Возьмем интеграл по данному интервалу:
.
Для равномерной сетки и четного числа шагов n формула Симпсона принимает вид:
Алгоритм метода Симпсона
Вводим исходные значения , a, b.
Задаем n=1, S=0.
Приравниваем S0=S, .n=2·n.
Расчет h=(b-a)/n.
Расчет приближенного значения интеграла:
6. Проверка условия |S0-S| ε. Если условие выполняется, то переход к пункту 7, иначе переход к пункту 3.
7. Расчет закончен. Результат равен S.
Реализация метода в MS Excel
Вычислить
с точностью =0,001.
Заполнение клеток листа MS Excel для n=2:
| Адрес клетки | Содержание | Тип |
| A1 | n=2 | Текст |
| A2 | a= | Текст |
| B2 | 0 | Число |
| A3 | b= | Текст |
| B3 | 0,5 | Число |
| A4 | h= | Текст |
| B4 | =(B3-B2)/2 | Формула |
| A6 | x | Текст |
| B6 | f | Текст |
| A7 | =B2 | Формула |
| B7 | =EXP(-A7*A7/2) | Формула |
| A8 | =A7+$B$4 | Формула |
| B8 | =EXP(-A8*A8/2) | Формула |
| A9 | =A8+$B$4 | Формула |
| B9 | =EXP(-A9*A9/2) | Формула |
| A10 | S= | Текст |
| B10 | =B4/3*(B7+4*B8+B9) | Формула |
Вид листа MS Excel:
Ответ: 0,479952.
Заполнение клеток листа MS Excel для n=4:
| Адрес клетки | Содержание | Тип |
| D1 | n=4 | Текст |
| D2 | a= | Текст |
| E2 | 0 | Число |
| D3 | b= | Текст |
| E3 | 0,5 | Число |
| D4 | h= | Текст |
| E4 | =(E3-E2)/4 | Формула |
| D6 | x | Текст |
| E6 | f | Текст |
| D7 | =E2 | Формула |
| E7 | =EXP(-D7*D7/2) | Формула |
| D8 | =D7+$E$4 | Формула |
| D9:D11 | Автозаполнение формулой из клетки D8 | Формула |
| E8:E11 | Автозаполнение формулой из клетки Е7 | Формула |
| D12 | S= | Текст |
| E12 | =E4/3*(E7+E11+4*(E8+E10)+2*E9) | Формула |
Вид листа MS Excel:
Ответ: 0,479927.
Далее выполняем расчеты для n=8,16.
В клетку H16 вводим формулу =H4/3*(H7+H15+4*(H8+H10+H12+H14)+2*(H9+H11+H13)).
Вид листа MS Excel для n=8:
Ответ: 0,479925.
В клетку К24 вводим формулу
=K4/3*(K7+K23+4*(K8+K10+K12+K14+K16+K18+K20+K22)+2*(K9+K11+K13+ K15+K17+K19+K21))
Вид листа MS Excel для n=16:
Ответ: 0,479925.
Вид таблицы результатов:
Проанализировав значения в этой таблице, увидим, что требуемая точность 0,001 достигнута сразу после первой итерации.







 Постановка задачи
Постановка задачи  – формула Ньютона-Лейбница.
– формула Ньютона-Лейбница.



 dx с точностью =0,001.
dx с точностью =0,001.
























