

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая программа по математике для направления подготовки 38.02.01 Экономика и бухгалтерский учет (2 курс)
календарно-тематическое планирование по математике
Просмотр содержимого документа
«Рабочая программа по математике для направления подготовки 38.02.01 Экономика и бухгалтерский учет (2 курс)»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
Профессиональное образовательное учреждение
«Гуманитарный педагогический колледж» (ГПК)
УТВЕРЖДАЮ
Директор ПОУ «Гуманитарный педагогический колледж».
___________М.Ханмагомедов
«___» __________ 2017г.
Рабочая программа дисциплины
ЕН.01 Математика
Направление профессиональной подготовки: 38.02.01 Экономика и бухгалтерский учет
Форма обучения: очно/заочная
Программа подготовки: углубленная (на базе основного общего образования)
Махачкала 2017
Автор (ы): преподаватель математики ПОУ «ГПК» Исаева П.М.
Рецензент:
Зайнулабидов Г.М., кандидат физ.-мат. наук, доцент кафедры экономики и информационных технологий ОУ ВО «ДГИ»
Программа утверждена на:
Заседании ПЦК естественнонаучного цикла (протокол №___от «___» 2017 г.)
Председатель ПЦК естественнонаучных дисциплин
Рабаданова А.М. _______________________ (подпись) (дата)
Зам. директора по УМР Идрисова А.Х_____________(подпись)______ (дата)
Согласованно
Представитель работодателя:
Генеральный директор ТНВ «ЛяРиба Финанс»____________ Алискеров М.С
(подпись) (Ф.И.О.)
Цель освоения дисциплины
Цель дисциплины:
Дисциплина ЕН.01 «Математика» должна вооружить студента математическими знаниями, необходимыми для изучения ряда общенаучных дисциплин и дисциплин профессионального цикла, создать фундамент математического образования, необходимый для получения профессиональных компетенций, воспитать математическую культуру и понимание роли математики в различных сферах профессиональной деятельности.
Задачи дисциплины:
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
- обучение студентов методам математического анализа, необходимых им при изучении остальных курсов;
- привитие студентам навыков исследования с использованием математического анализа;
- обучение студентов методам логически строгого построения доказательств;
- формирование навыков и умений, необходимых при практическом применении математических идей и методов для анализа и моделирования сложных систем, процессов, явлений, для поиска оптимальных решений и выбора наилучших способов реализации..
2. Место дисциплины в структуре ППССЗ:
Дисциплина ЕН.01 Математика относится к Математическому и общему естественнонаучному циклу профильных дисциплин образовательной программы направления подготовки 38.02.01 Экономика и бухгалтерский учет
3. Компетенции обучающихся, формируемые в результате освоения дисциплины ЕН.01 Математика.
| Формируемые компетенции | Осваиваемые знания, умения | ||
| Код | Наименование |
| |
|
| Общекультурные компетенции (ОК) | ||
| ОК-2 | Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. | Знать: методики решения задач | |
| Уметь: применять знания на практике
| |||
| Владеть: самостоятельно решает возникающие задачи
| |||
| ОК-4 | Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития. | Знать: самостоятельно искать, извлекать, систематизировать, анализировать и отбирать необходимую для решения учебных задач | |
| Уметь: ориентироваться в информационных потоках, умеет выделять в них главное и необходимое | |||
| Владеть: письменной и устной коммуникацией на математическом языке
| |||
| ОК-5 | Владеть информационной культурой, анализировать и оценивать информацию с использованием информационно-коммуникационных технологий. | Знать: современные средства получения и передачи информации и информационные и телекоммуникационные технологии (аудио-, видеозапись, электронная почта, СМИ, Интернет). Уметь: работать с книгами, учебниками, справочниками, атласами, картами, определителями, энциклопедиями, каталогами, словарями, CD-Rom, Интернет Владеть: разными видами информации: диаграммами, символами, графиками, текстами, таблицами и т.д. | |
| ОК-8 | Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. | Знать: стремление совершенствованию Уметь: саморазвиваться Владеть: самостоятельно повышает квалификацию | |
| Профессиональные компетенции (ПК) | |||
| ПК-1.1 | Обрабатывать первичные бухгалтерские документы. | Знать: основные математические методы решения прикладных задач в области профессиональной деятельности Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-1.2 | Разрабатывать и согласовывать с руководством организации рабочий план счетов бухгалтерского учета организации. | Знать: основные математические методы решения прикладных задач в области профессиональной деятельности Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-1.3 | Проводить учет денежных средств, оформлять денежные и кассовые документы. | Знать: основные математические методы решения прикладных задач в области профессиональной деятельности Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-1.4 | Формировать бухгалтерские проводки по учету имущества организации на основе рабочего плана счетов бухгалтерского учета. | Знать: основные математические методы решения прикладных задач в области профессиональной деятельности Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-2.1 | Формировать бухгалтерские проводки по учету источников имущества организации на основе рабочего плана счетов бухгалтерского учета. | Знать: основные математические методы решения прикладных задач в области профессиональной деятельности Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-2.3 | Отражать в бухгалтерских проводках зачет и списание недостачи ценностей (регулировать инвентаризационные разницы) по результатам инвентаризации. | Знать: основные математические методы решения прикладных задач в области профессиональной деятельности Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-2.4 | Проводить процедуры инвентаризации финансовых обязательств организации. | Знать: основные методические методы решения прикладных задач в области профессиональной деятельности Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-3.1 | Формировать бухгалтерские проводки по начислению и перечислению налогов и сборов в бюджеты различных уровней. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-3.2 | Оформлять платежные документы для перечисления налогов и сборов в бюджет, контролировать их прохождение по расчетно-кассовым банковским операциям. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-3.3 | Формировать бухгалтерские проводки по начислению и перечислению страховых взносов во внебюджетные фонды. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-3.4 | Оформлять платежные документы на перечисление страховых взносов во внебюджетные фонды, контролировать их прохождение по расчетно-кассовым банковским операциям. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-4.1 | Отражать нарастающим итогом на счетах бухгалтерского учета имущественное и финансовое положение организации, определять результаты хозяйственной деятельности за отчетный период. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности: | |
| ПК-4.2 | Составлять формы бухгалтерской отчетности в установленные законодательством сроки. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-4.3 | Составлять налоговые декларации по налогам и сборам в бюджет, налоговые декларации по Единому социальному налогу (ЕСН) и формы статистической отчетности в установленные законодательством сроки. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности | |
| ПК-4.4 | Проводить контроль и анализ информации об имуществе и финансовом положении организации, ее платежеспособности и доходности. | Знать: основные принципы построения экономической системы организации Уметь: решать прикладные задачи в области профессиональной деятельности | |
В результате освоения дисциплины обучающийся должен
уметь:
-решать прикладные задачи в области профессиональной деятельности;
-решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления;
-находить аналитическое выражение производной по табличным данным;
-решать простейшие дифференциальные уравнения;
-выполнять операции над множествами;
-совершать арифметические операции над матрицами;
-находить определитель матрицы;
-решать системы уравнений методами Крамера, Гаусса, методом обратной матрицы;
-совершать операции с комплексными числами;
-решать простейшие задачи, используя элементы теории вероятности и математической статистики.
В результате освоения дисциплины обучающийся должен
знать:
-значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы;
-основные математические методы решения прикладных задач в области профессиональной деятельности;
-основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
-основы интегрального и дифференциального исчисления.
3. Структура и содержание дисциплины
Общая трудоемкость дисциплины составляет 96 ч. В том числе:
Структура дисциплины
| № п/п | Наименование раздела дисциплины | Семестр | недель | Виды учебной работы (в академических часах) |
Всего | |||
| Л | ПЗ | ЛБ | CP | |||||
| 1. | Раздел 1. Математический анализ | 3 |
| 6 | 6 |
| 4 | 16 |
| 2. | Раздел 2. Основы дискретной математики | 3 |
| 4 | 4 |
| 6 | 14 |
| 3. | Раздел 3. Элементы линейной алгебры | 3 |
| 6 | 4 |
| 6 | 16 |
| 4. | Раздел 4. Теория комплексных чисел | 4 |
| 8 | 8 |
| 8 | 24 |
| 5. | Раздел 5 Основы теории вероятностей и математической статистики | 4 |
| 8 | 10 |
| 8 | 26 |
|
| Всего |
|
| 32 | 32 |
| 32 | 96 |
|
| Вид промежуточной аттестации (зачет, экзамен) | Контрольная работа, дифф.зачет | ||||||
Заочная форма обучения
| № п/п | Наименование раздела дисциплины | Семестр | недель | Виды учебной работы (в академических часах) |
Всего | |||
| Л | ПЗ | ЛБ | CP | |||||
| 1. | Раздел 1. Математический анализ | 3 |
| 2 | 2 |
| 2 | 6 |
| 2. | Раздел 2. Основы дискретной математики | 3 |
| 2 | 2 |
| 2 | 6 |
| 3. | Раздел 3. Элементы линейной алгебры | 3 |
| 2 | 2 |
| 2 | 6 |
| 4. | Раздел 4. Теория комплексных чисел | 4 |
| 2 | 2 |
| 2 | 6 |
| 5. | Раздел 5 Основы теории вероятностей и математической статистики | 4 |
| 2 | 2 |
| 2 | 6 |
|
| Всего |
|
| 10 | 10 |
| 10 | 30 |
|
| Вид промежуточной аттестации (зачет, экзамен) | Дифференцированный зачет | ||||||
Содержание дисциплины
(Очная форма обучения)
| № п/п | Наименование раздела дисциплины | Содержание раздела (дидактические единицы) | Кол. часов | Форма контроля | В интер. форме | Реализ. копмет. |
| 1. | Раздел 1. Математический анализ | Содержание учебного материала: Функции одной независимой переменной. Пределы. Непрерывность функций. Производная, геометрический смысл. Исследование функций. Неопределенный интеграл. Непосредственное интегрирование. Замена переменной. Определенный интеграл. Вычисление определенного интеграла. Геометрический смысл определенного интеграла. Функции нескольких переменных. Приложение интеграла к решению прикладных задач. Частные производные.
| 12 | КР | Демонстрация материалов урока с помо-щью ИТО | ОК-2,4,5,8 ПК-1.1; ПК-1.2 ПК-1.3 ПК-1.4 ПК-2.1 ПК-2.2 ПК-2.3 ПК-2.4 ПК-3.1 ПК-3.2 ПК-3.3. ПК-4.1 ПК-4.4 ПК-4.2 |
|
| Тема 1.1. Дифференциальное и интегральное исчисление
| Практические занятия: 1Производная функции. Правила вычисления производных. Вычисление пределов функций с использованием первого и второго замечательного пределов. Исследование функций на непрерывность. Нахождение производных по алгоритму. Вычисление производной сложных функций. Интегрирование простейших функций. Вычисление простейших определенных интегралов. Решение прикладных задач. Самостоятельная работа обучающихся: Производная, ее геометрический смысл. Непрерывность функций. Асимптоты. Неопределенный интеграл. Геометрический смысл определенного интеграла. | 4 | КР |
|
|
|
| Тема 1.2. Обыкновенные дифференциальные уравнения | Содержание учебного материала: Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами. Практические занятия: Решение дифференциальных уравнений с разделяющимися переменными. Решение прикладных задач. Самостоятельная работа обучающихся: Решение однородных дифференциальных уравнений первого порядка. Решение линейных однородных уравнений второго порядка. | 4 | КР |
|
|
|
| Тема1.3. Дифференциальные уравнения в частных производных | Содержание учебного материала: Простейшие дифференциальные уравнения в частных производных. Дифференциальные уравнения линейные относительно частных производных. Самостоятельная работа обучающихся: Решение простейших дифференциальных уравнений линейных относительно частных производных. | 4 | КР |
|
|
| 2. | Раздел 2. Основы дискретной математики | Содержание учебного материала: Элементы и множества. Задание множеств. Операции над множествами. Свойства операций над множествами. Отношения. Свойства отношений.
| 8 | КР |
| ОК-2,4,5,8 ПК-1.1; ПК-1.2 ПК-1.3 ПК-1.4 ПК-2.1 ПК-2.2 ПК-2.3 ПК-2.4 ПК-3.1 ПК-3.2 ПК-3.3. ПК-4.1 ПК-4.4 ПК-4.2 |
|
| Тема 2.1. Множества и отношения. Свойства отношений. Операции над множествами | Практические занятия: Операции над множествами. Самостоятельная работа обучающихся: Отношения; свойства отношений.
| 8 | КР |
|
|
| 3. | Раздел 3. Элементы линейной алгебры | Содержание учебного материала: Матричные модели. Операции над матрицами. Транспонированная матрица. Обратная матрица. Определитель матрицы. Правило треугольников.
| 10 | КР |
| ОК-2,4,5,8 ПК-1.1; ПК-1.2 ПК-1.3 ПК-1.4 ПК-2.1 ПК-2.2 ПК-2.3 ПК-2.4 ПК-3.1 ПК-3.2 ПК-3.3. ПК-4.1 ПК-4.4 ПК-4.2 |
|
| Тема3.1. Основные понятия теории матриц | Практические занятия: Вычисление суммы и разности матриц. Умножение матрицы на число. Умножение двух матриц. Вычисление определителя матриц. Самостоятельная работа обучающихся: Нахождение обратных матриц. Нахождение транспонированных матриц. Вычисление определителя матриц второго порядка. | 4 | КР |
|
|
|
| Тема 3.2. Решение матричных уравнений. | Содержание учебного материала: Решение систем линейных уравнений методами Гаусса, Крамера. Решений систем линейных уравнений методом обратной матрицы. Практические занятия: Нахождение решений систем линейных уравнений тремя методами. Самостоятельная работа обучающихся: Решение матричных уравнений. Контрольная работа: «Математический анализ. Матричные уравнения» | 6 | КР |
|
|
| 4. | Раздел 4. Теория комплексных чисел | Содержание учебного материала: Понятие комплексных чисел. Мнимая единица. Арифметические операции над комплексными числами. Сопряженное комплексное число. Комплексные числа на координатной плоскости. Геометрические модели комплексных чисел.
| 16 | КР |
| ОК-2,4,5,8 ПК-1.1; ПК-1.2 ПК-1.3 ПК-1.4 ПК-2.1 ПК-2.2 ПК-2.3 ПК-2.4 ПК-3.1 ПК-3.2 ПК-3.3. ПК-4.1 ПК-4.4 ПК-4.2 |
|
| Тема 4.1 Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость. | Практические занятия: Операции над комплексными числами. Изображение на координатной плоскости комплексных чисел. Самостоятельная работа обучающихся: Работа с комплексными числами. | 6 | КР |
|
|
|
| Тема 4.2 Тригонометрическая форма записи комплексного числа | Содержание учебного материала: Модуль комплексного числа. Модуль произведения комплексных чисел. Комплексное число на числовой окружности. Тригонометрическая форма записи комплексного числа. Аргумент комплексного числа. Практические занятия: Нахождение модуля комплексного числа. Нахождение аргумента комплексного числа. Запись комплексного числа в стандартной тригонометрической форме. | 4 | КР |
|
|
|
| Тема 4.3 Комплексные числа и квадратные уравнения. Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа | Содержание учебного материала: Квадратный корень из комплексного числа. Алгоритм извлечения квадратного корня из комплексного числа. Формула Муавра. Возведение комплексного числа в n – ю степень. Кубический корень из комплексного числа. Алгоритм извлечения кубического корня из комплексного числа. Практические занятия: Решение квадратных уравнений. Вычисление квадратного корня из комплексного числа. Возведение в степень комплексных чисел. Вычисление кубического корня из комплексного числа. Самостоятельная работа обучающихся: Выполнение действий с комплексными числами | 6 | КР |
|
|
| 5. | Раздел 5 Основы теории вероятностей и математической статистики | Содержание учебного материала: Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятностей. Элементы комбинаторики | 18 | КР |
| ОК-2,4,5,8 ПК-1.1; ПК-1.2 ПК-1.3 ПК-1.4 ПК-2.1 ПК-2.2 ПК-2.3 ПК-2.4 ПК-3.1 ПК-3.2 ПК-3.3. ПК-4.1 ПК-4.4 ПК-4.2 |
|
| Тема 5.1. Основные понятия теории вероятностей. | . Практические занятия: Решение задач по теории вероятности. Самостоятельная работа обучающихся: Теорема умножения вероятностей. | 8 | КР |
|
|
|
| Тема 5.2.Основы математической статистики. | Содержание учебного материала Основные понятия и задачи математической статистики. Практическое занятие: Решение задач математической статистики. Самостоятельная работа обучающихся: Решение задач математической статистики. Контрольная работа «Матричные уравнения. Теория комплексных чисел. Основы теории вероятностей и математической статистики» | 10 | КР |
|
|
Образовательные технологии
| № п/п | Вид и тема занятий (лекция, пр.р., л/р.) | Используемые интерактивные технологии | Колич. часов | |
| 1 | Лекция:1 Тема: Дифференциальное и интегральное исчисление | Демонстрация материалов урока с помощью ИТО | 4 | |
| Практическое занятие (семинар): Форма проведения: решение задач | ||||
| 2 | Лекция 2. Обыкновенные дифференциальные уравнения | Демонстрация материалов урока с помощью ИТО | 2 | |
| Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 2 | ||
| 3 | Лекция 3. Дифференциальные уравнения в частных производных | Демонстрация материалов урока с помощью ИТО | 2 | |
| Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 2 | ||
| 4 | Лекция 4. Тема 2.1. Множества и отношения. Свойства отношений. Операции над множествами | Демонстрация материалов урока с помощью ИТО | 4 | |
| 5 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 4 | |
| 6 | Лекция 5. Основные понятия теории матриц | Демонстрация материалов урока с помощью ИТО | 4 | |
| 7 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 2 | |
| 8 | Лекция 6. Тема 3.2.Решение матричных уравнений | Демонстрация материалов урока с помощью ИТО | 2 | |
| 9 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 2 | |
| 10 | Лекция Тема 4.1 Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость. | Демонстрация материалов урока с помощью ИТО | 2 | |
| 11 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 2 | |
| 12 | Лекция Тема 4.2 Тригонометрическая форма записи комплексного числа | Демонстрация материалов урока с помощью ИТО | 4 | |
| 13 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 4 | |
| 14 | Лекция Тема 4.3 Комплексные числа и квадратные уравнения. Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа | Демонстрация материалов урока с помощью ИТО | 2 | |
| 15 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 2 | |
| 16 | Лекция Тема 5.1. Основные понятия теории вероятностей. | Демонстрация материалов урока с помощью ИТО | 8 | |
| 17 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помо-щью ИТО |
| |
| 18 | Лекция Тема 5.2.Основы математической статистики. | Демонстрация материалов урока с помощью ИТО | 8 | |
| 19 | Практическое занятие (семинар): Форма проведения: решение задач | Демонстрация материалов урока с помощью ИТО | 10 | |
| Всего | 64 | |||
6. Самостоятельная работа студентов.
(Очная форма обучения)
| №п/п | Наименование раздела дисциплины | Вид самостоятельной работы | Трудоемкость (в академических часах) | Форма отчетности |
| 1. | Раздел 1. Математический анализ
| Самостоятельная работа обучающихся: Производная, ее геометрический смысл. Непрерывность функций. Асимптоты. Неопределенный интеграл. Геометрический смысл определенного интеграла. Самостоятельная работа обучающихся: Решение однородных дифферен-циальных уравнений первого порядка. Решение линейных однородных уравнений второго порядка. | 4
| КР |
| 2. | Раздел 2. Основы дискретной математики | Самостоятельная работа обучающихся: Отношения; свойства отношений | 6 | кроссворд |
| 3. | Раздел 3. Элементы линейной алгебры
| Самостоятельная работа обучающихся: Нахождение обратных матриц. Нахождение транспонированных матриц. Вычисление определителя матриц второго порядка.
Самостоятельная работа обучающихся: Решение матричных уравнений. | 6 | КР |
| 4. | Раздел 4. Теория комплексных чисел | Самостоятельная работа обучающихся: Работа с комплексными числами. | 8 | Тест |
| 5. | Раздел 5 Основы теории вероятностей и математической статистики | Самостоятельная работа обучающихся: Решение задач математической статистики. | 8 | КР |
|
| Всего |
| 32 |
|
Заочная форма обучения
| №п/п | Наименование раздела дисциплины | Вид самостоятельной работы | Трудоемкость (в академических часах) | Форма отчетности |
| 1. | Раздел 1. Математический анализ
| Самостоятельная работа обучающихся: Производная, ее геометрический смысл. Непрерывность функций. Асимптоты. Неопределенный интеграл. Геометрический смысл определенного интеграла. Самостоятельная работа обучающихся: Решение однородных дифферен-циальных уравнений первого порядка. Решение линейных однородных уравнений второго порядка. | 4
| КР |
| 2. | Раздел 2. Основы дискретной математики | Самостоятельная работа обучающихся: Отношения; свойства отношений | 6 | кроссворд |
| 3. | Раздел 3. Элементы линейной алгебры
| Самостоятельная работа обучающихся: Нахождение обратных матриц. Нахождение транспонированных матриц. Вычисление определителя матриц второго порядка.
Самостоятельная работа обучающихся: Решение матричных уравнений. | 6 | КР |
| 4. | Раздел 4. Теория комплексных чисел | Самостоятельная работа обучающихся: Работа с комплексными числами. | 8 | Тест |
| 5. | Раздел 5 Основы теории вероятностей и математической статистики | Самостоятельная работа обучающихся: Решение задач математической статистики. | 8 | КР |
|
| Всего |
| 32 |
|
7. Текущий контроль успеваемости и промежуточная аттестация
7.1 Текущий контроль успеваемости
| №
| Текущий контроль успеваемости |
| 1. | Тестовые задания
|
| 2. | Практические задания Тема: Пределы Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
|
| 3. | Темы для самостоятельного изучения |
7.2. Промежуточная аттестация в форме дифференцированного зачета
| № | Темы курсовых работ/проектов, рефератов, вопросы и задания | |||||||||||||||||||||||||||||||||
| 1 | Темы рефератов
| |||||||||||||||||||||||||||||||||
| 2 | Тест по всему объему дисциплины Производная и ее применение. 1. Найдите производную функции: А) В) С) D) Е) 2. Найдите производную функции: А) В) С) D) Е) 3. Найдите производную функции: А) В) С) D) Е) 4. Найдите в точке А) 4 В) С) 0 D) -3 Е) 5. Производная функции А) В) С) D) Е) 6. Дана функция А) 1 В) 2 С) 3 D) 0 Е) 4 7. Найдите критические точки функции А) 0,5;2 В) -1,5;2 С) -1;3 D) -1,5;-2 Е) -2;1,5 8. Производная функции А) В) С) D) Е) 9. Вычислите значение производной функции: А) В) С) D) Е) 10. Точкой, в которой выполняются необходимые условиея существования экстремума функции А) В) С) D) Е) 11. Найдите в точке А) В) С) D) 1 Е) 12. Если А) 1 В) 0 С) -1 D) 3 Е) 2 13. Найдите производную функции: А) В) С) D) Е) 14. Найдите производную функции: А) В) С) D) Е) 15. Найдите а) наименьшее; б) наибольшее значения функции A) а) -3, б) 40 B) а) 3, б) 40 C) а) -40, б) -3 D) а) -38, б)-2 E) а) -40, б) 3 16. Какой угол образуют с направлением оси Ох касательная к графику A) B) Прямой C) Острый D)Тупой E) 17. В каких точках касательная к графику функции А) В) С) D) Е) 18. Найдите наибольшее и наименьшее значения функции А) В) С) D) Е) Тест 2 Первообразная и интеграл Вариант 1 А1. Выберите первообразную для функции 1)
А2. Какая из данных функций не является первообразной для функции 1) А3. Найдите общий вид первообразных для функции 1) А4. Вычислите интеграл А5. Вычислите интеграл А6. Вычислите интеграл
А7. Найдите площадь фигуры, ограниченной линиями 1)
А8. Найдите площадь фигуры, изображенной на рисунке 1. 1)
А9. Найдите площадь фигуры, изображенной на рисунке 2.
1) Рис. 2 Тест 3 Первообразная и интеграл Вариант 2 А1. Выберите первообразную для функции 1) А2. Какая из данных функций не является первообразной для функции 1) А3. Найдите общий вид первообразных для функции 1) А4. Вычислите интеграл А5. Вычислите интеграл А6. Вычислите интеграл
А7. Найдите площадь фигуры, ограниченной линиями 1)
А8. Найдите площадь фигуры, изображенной на рисунке 1. 1)
А9. Найдите площадь фигуры, изображенной на рисунке 2.
1) Рис. 2
А10. Найдите площадь фигуры, изображенной на рисунке 3.
1) Рис. 3
Ответы:
«Функция. Предел функции» Инструктаж: выбрать один правильный ответ 1.Для обозначения различных меняющихся величин применяют термин а) функция 2.Переменная Х - это а) функция 3.Если дана зависимость между переменными и каждому Х однозначно определено значение У то это а) функция 4.Область определения функции – это множество всех а) возможных значений У 5.Область определения функции обозначают буквой а) А 6.Множество точек плоскости с координатами (х, f(х)) называется а) графиком функции f 7.Множество всех возможных значений переменной Х - это а) область определения функции 8.Линейную функцию определяет зависимость вида а) C/х 9.Квадратичную функцию определяет зависимость вида а) C/х 10.Дробно-линейную функцию определяет зависимость вида а) C/х 11.Числовая последовательность – это выражение вида а) (х, f(х)) 12.Число А называется пределом функции F(x) в точке Х0, когда к А сходится последовательность из значений а) аргумента 13.Число А называется пределом функции в точке Х0, когда к Х0 сходится последовательность из значений а) аргумента 14. Символическое обозначение предела функции при х Х0 а) lim f(x) = А б) lim f(x) = А в) lim f(x) = А г) lim f(x) = А x Х - x ∞ x Х+ x Х0 15. Символическое обозначение левого предела функции а) lim f(x) = А б) lim f(x) = А в) lim f(x) = А г) lim f(x) = А x Х- x ∞ x Х+ x Х0 16. Символическое обозначение предела функции при х ∞ а) lim f(x) = А б) lim f(x) = А в) lim f(x) = А г) lim f(x) = А -Теория вероятности Вариант 1
| |||||||||||||||||||||||||||||||||
| 3 | Вопросы аттестации (зачет, экзамен) Вопросы к промежуточному и итоговому контролю: 1. Множества. Операции над множествами. 2. Ограниченные множества. Грани множества. 3. Последовательности. Сходящиеся последовательности. 4. Свойства сходящихся последовательностей. 5. Функция. Способы задания функции. Сложная и обратная функции. 6. Ограниченные и монотонные функции, свойства. 7. Четные и нечетные функции, свойства. 8. Периодические функции, свойства. 9. Предел функции (в конечной точке, в бесконечной точке). Геометрическая иллюстрация. 10. Односторонние пределы. Теорема о связи предела и односторонних пределов. 11. Основные теоремы о пределах (теорема о единственности предела; об ограниченности функции, имеющей предел; теорема о предел сложной функции). 12. Бесконечно малые функции (б.м.ф.) Свойства б.м.ф. (теоремы о сумме, произведении б.м.ф.) 13. Теоремы о пределах функций, связанные с арифметическими операциями. 14. Теоремы о пределах функций, связанные с неравенствами (теорема о переходе к пределу в неравенстве, теорема о пределе промежуточной функции). 15. Первый замечательный предел. 16. Второй замечательный предел. 17. Сравнение бесконечно малых функций (б.м.ф.). Принцип замены эквивалентных б.м.ф. 18. Сравнение бесконечно малых функций (б.м.ф.). Принцип отбрасывания б.м.ф. высших порядков. 19. Непрерывность функции в точке (определения на языке приращений). Односторонняя непрерывность в точке. 20. Теоремы об арифметических операциях над непрерывными функциями. 21. Непрерывность функции на множестве. Теоремы о свойствах непрерывных функций на отрезке ( без доказательства). 22. Точки разрыва функции и их классификация. 23. Производная функции в точке. Табличное дифференцирование. Необходимое условие существования производной. 24. Правила дифференцирования суммы, произведения, отношения. 25. Геометрический и механический смысл производной. 26. Уравнение касательной и нормали к графику функции. 27. Теорема о производной сложной функции. 28. Логарифмическое дифференцирование. 29. Теорема о производной обратной функции. 30. Производная параметрически заданной функции. 31. Дифференцируемость функции в точке. Критерий дифференцируемости в точке. 32. Дифференциал функции, его свойства. 33. Геометрический смысл дифференциала. Применение дифференциала в приближенных вычислениях. 34. Свойство инвариантности записи дифференциала. 35. Производные и дифференциалы высших порядков. 36. Теорема Ролля. 37. Теорема Лагранжа. Формула конечных приращений. 38. Теорема Коши. 39. Правило Лопиталя раскрытия неопределенностей. 40. Формула Тейлора. Различные формы остаточного члена. 41. Возрастание и убывание функций. Достаточное условие. 42. Экстремум функции. Необходимое условие экстремума. Достаточные условия экстремума. 43. Наибольшее и наименьшее значение функции на отрезке. | |||||||||||||||||||||||||||||||||
| 4 | | |||||||||||||||||||||||||||||||||
| 5 |
|
8. Основная и дополнительная литература
Основные источники:
1. Богомолов Н.В. Математика. – М.: Издательский центр «Высшая школа», 2012.
2. Богомолов Н.В. Практические занятия по математики.- М.: Издательский центр «Высшая школа», 2012.
Яковлев Г.Н., Математика для ССУЗов, в 2 частях, М: Новая волна, 2010 г.
4. Григорьев С.Г., Иволгина С.В. Математика. – М.: Издательский центр «Академия», 2011.
5. Дадаян А.А. Сборник задач по математике. – М.: Издательский центр «ФОРУМ: ИНФРА», 2011.
6. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика. – М.: Издательский центр «Академия», 2011.
Дополнительные источники:
Бычков А.Г. Сборник задач по теории вероятностей, математической статистики и методам оптимизации. – М.: Издательский центр «ФОРУМ», 2010.
Беспалова Г.А. Сборник дидактических заданий по дисциплине «Математика»,2010
Григорьев В.П., Дубинский Ю.А. Элементы высшей математики. – М.:
Издательский центр «Академия», 2010.
Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике. – М.: Издательский центр «Академия», 2010.
Спирина М.С., Спирин П.А. Дискретная математика. – М.: Издательский центр «Академия», 2010.
9. Перечень ресурсов информационно-телекоммуникационной сети «Интернет», необходимых для освоения дисциплины (модуля)
Интернет-ресурсы:
Конев В.В., Линейная алгебра: электронный учебник. Форма доступа:
http://portal.tpu.ru:7777/SHARED/k/KONVAL/Sites/Russian_sites/index1.htm
Конев В.В., Пределы последовательностей и функций: электронный учебник
Форма доступа:
http://portal.tpu.ru:7777/SHARED/k/KONVAL/Sites/Russian_sites/01.htm
Российская государственная библиотека. Форма доступа: http://www.rsl.ru
Теория вероятностей, математическая статистика и их приложения:
электронные книги, статьи. Форма доступа: http://www.teorver.ru/
10. Методические указания для обучающихся по освоению дисциплины (модуля)
| Результаты обучения (освоенные умения, усвоенные знания) | Формы и методы контроля и оценки результатов обучения |
| Освоенные умения:
Усвоенные знания:
|
практическое занятие, самостоятельная работа
выполнение заданий, комбинированный опрос
выполнение письменных заданий, фронтальный опрос
выполнение индивидуальных заданий по карточкам
выполнение контрольных и самостоятельных заданий
практические занятия, внеаудиторная самостоятельная работа, фронтальный опрос
практические занятия, выполнение контрольной работы |
Аннотация
рабочей программы дисциплины ЕН.01 Математика
Направление подготовки: 38.02.01 Экономика и бухгалтерский учет
Квалификация: бухгалтер
1. Цель и задачи освоения дисциплины
Цель дисциплины:
Дисциплина «Математика» должна вооружить студента математическими знаниями, необходимыми для изучения ряда общенаучных дисциплин и дисциплин профессионального цикла, создать фундамент математического образования, необходимый для получения профессиональных компетенций, воспитать математическую культуру и понимание роли математики в различных сферах профессиональной деятельности.
Задачи дисциплины:
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
- обучение студентов методам математического анализа, необходимых им при изучении остальных курсов;
- привитие студентам навыков исследования с использованием математического анализа;
- обучение студентов методам логически строгого построения доказательств;
- формирование навыков и умений, необходимых при практическом применении математических идей и методов для анализа и моделирования сложных систем, процессов, явлений, для поиска оптимальных решений и выбора наилучших способов реализации..
.
2. Место дисциплины в структуре ППССЗ
Дисциплина ЕН.01 Математика относится к Математическому и общему естественнонаучному циклу профильных дисциплин образовательной программы направления 38.02.01 Экономика и бухгалтерский учет
3. Программа дисциплины «Математика».
Раздел 1. Математический анализ
Раздел 2.Основы дискретной математики
Раздел 3. Элементы линейной алгебры
Раздел 4.Теория комплексных чисел
Раздел 5 Основы теории вероятностей и математической статистики
4. Требования к результатам освоения дисциплины «Математика».
4.1. Процесс изучения дисциплины ЕН.01 Математика направлен на формирование следующих компетенций обучающихся (в соответствии с ФГОС СПО и требованиями к результатам освоения основной образовательной программы (ППССЗ):
| Формируемые компетенции | |
| Код | Наименование |
|
| |
| ОК-2 | Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. |
| ОК-4 | Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития. |
| ОК-5 | Владеть информационной культурой, анализировать и оценивать информацию с использованием информационно-коммуникационных технологий. |
| ОК-8 | Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. |
| ПК-1.1 | Обрабатывать первичные бухгалтерские документы. |
| ПК-1.2 | Разрабатывать и согласовывать с руководством организации рабочий план счетов бухгалтерского учета организации. |
| ПК-1.3 | Проводить учет денежных средств, оформлять денежные и кассовые документы. |
| ПК-1.4 | Формировать бухгалтерские проводки по учету имущества организации на основе рабочего плана счетов бухгалтерского учета. |
| ПК-2.1 | Формировать бухгалтерские проводки по учету источников имущества организации на основе рабочего плана счетов бухгалтерского учета. |
| ПК-2.3 | Отражать в бухгалтерских проводках зачет и списание недостачи ценностей (регулировать инвентаризационные разницы) по результатам инвентаризации. |
| ПК-2.4 | Проводить процедуры инвентаризации финансовых обязательств организации. |
| ПК-3.1 | Формировать бухгалтерские проводки по начислению и перечислению налогов и сборов в бюджеты различных уровней. |
| ПК-3.2 | Оформлять платежные документы для перечисления налогов и сборов в бюджет, контролировать их прохождение по расчетно-кассовым банковским операциям. |
| ПК-3.3 | Формировать бухгалтерские проводки по начислению и перечислению страховых взносов во внебюджетные фонды. |
| ПК-3.4 | Оформлять платежные документы на перечисление страховых взносов во внебюджетные фонды, контролировать их прохождение по расчетно-кассовым банковским операциям. |
| ПК-4.1 | Отражать нарастающим итогом на счетах бухгалтерского учета имущественное и финансовое положение организации, определять результаты хозяйственной деятельности за отчетный период. |
| ПК-4.2 | Составлять формы бухгалтерской отчетности в установленные законодательством сроки. |
| ПК-4.3 | Составлять налоговые декларации по налогам и сборам в бюджет, налоговые декларации по Единому социальному налогу (ЕСН) и формы статистической отчетности в установленные законодательством сроки. |
| ПК-4.4 | Проводить контроль и анализ информации об имуществе и финансовом положении организации, ее платежеспособности и доходности. |
4.2. В результате освоения дисциплины «Математика» студент должен:
уметь:
-решать прикладные задачи в области профессиональной деятельности;
-решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления;
-находить аналитическое выражение производной по табличным данным;
-решать простейшие дифференциальные уравнения;
-выполнять операции над множествами;
-совершать арифметические операции над матрицами;
-находить определитель матрицы;
-решать системы уравнений методами Крамера, Гаусса, методом обратной матрицы;
-совершать операции с комплексными числами;
-решать простейшие задачи, используя элементы теории вероятности и математической статистики.
знать:
-значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы;
-основные математические методы решения прикладных задач в области профессиональной деятельности;
-основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
-основы интегрального и дифференциального исчисления
5. Общая трудоемкость дисциплины составляет 96 часов
6. Разработчик: преподаватель математики ПОУ « ГПК» Исаева П.М.
23




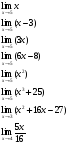

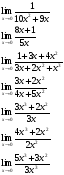




















 значение производной функции
значение производной функции 










