

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая программа по математике (алгебра) 9 класс
Рабочая программа разработана в соответствии с основными положениями федерального государственного образовательного стандарта основного общего образования, планируемыми результатами основного общего образования по математике, ориентирована на работу по учебно-методическому комплекту Дорофеева Г.В. Алгебра. 9 класс, М.: «Просвещение», 2016г.
Просмотр содержимого документа
«Рабочая программа по математике (алгебра) 9 класс»
Муниципальное общеобразовательное учреждение
«Лицей № 12»
«Принята» «Утверждена»
на заседании педагогического
совета, Протокол №1 Приказом №
от 30 августа 2016 г. от 31 августа 2016 г.
Председатель педагогического Директор МОУ «Лицей № 12»
совета
______________/ ____________/
РАБОЧАЯ ПРОГРАММА
по МАТЕМАТИКЕ (АЛГЕБРА)
(основное общее образование)
9 класс
2016 – 2017 учебный год
Учитель математики МОУ «Лицей №12»
Каримова Е. В.
г. Железногорск
2016 г.
Раздел 1. Пояснительная записка
Настоящая рабочая программа разработана в соответствии с основными положениями федерального государственного образовательного стандарта основного общего образования, планируемыми результатами основного общего образования по математике, требованиями Основной образовательной программы МОУ «Лицей №12» г. Железногорска и ориентирована на работу по учебно-методическому комплекту
Дорофеев Г.В.Алгебра. 9 класс: учебник / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова. -М.: «Просвещение», 2016г.
Видеман Т.Н. Поурочные планы. 9 класс. К учебному комплекту Г.В. Дорофеев (В помощь школьному учителю) –М.: Просвещение, 2009г.
Макарычев Ю.Н. Дидактические материалы по алгебре для 9 класса. –М.: Просвещение,2010г.
Учебно-методический комплект по математике. Алгебра 7-9 классы. (Электронное досье школьного учителя математики),2010г.
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития, учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Задачи учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
В рамках указанных содержательных линий решаются следующиезадачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул;
совершенствование практических навыков и вычислительной культуры; приобретение практических навыков, необходимых для повседневной жизни;
формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности;
развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений;
развитие воображения, способностей к математическому творчеству;
важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры;
формирование функциональной грамотности — умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты в простейших прикладных задачах.
Нормативные документы, в соответствии с которыми разработана рабочая программа:
Федеральный закон от 29.12.2012г. №273-ФЗ «Об образовании в Российской Федерации».
Основная образовательная программа МОУ «Лицей №12» г. Железногорска на 2016-2017 учебный год
Федеральный государственный образовательный стандарт основного общего образования /МО и науки РФ. – М.: Просвещение,2011г. -48с.-
Примерные программы основного общего образования. Математика. – (Стандарты второго поколения). – 3-е изд., перераб. – М.: Просвещение, 2011.
«Алгебра. Сборник рабочих программ 7 - 9 классы». Составитель Т. А. Бурмистрова.– М.: Просвещение, 2011. – 96 с.
Формирование универсальных учебных действий в основной школе. Система заданий / А. Г. Асмолов, О. А. Карабанова. – М.: Просвещение, 2010.
Раздел 2. Общая характеристика курса
Практическая направленность курса в достижении обучающимися планируемых личностных, метапредметных и предметных результатов.
Изучение математики в основной школе дает возможность учащимся достичь следующих результатов развития:
в личностном направлении:
уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контр примеры;
уметь распознавать логически некорректные высказывания, отличать гипотезу от факта, вырабатывать критичность мышления;
представлять математическую науку как сферу человеческой деятельности, представлять этапы её развития и значимость для развития цивилизации;
вырабатывать креативность мышления, инициативу, находчивость, активность при решении математических задач;
уметь контролировать процесс и результат учебной математической деятельности;
вырабатывать способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
в метапредметном направлении:
иметь первоначальное представление об идеях и методах математики как об универсальном языке науки и техники, о средствах моделирования явлений и процессов;
уметь видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
уметь выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
уметь применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимать сущность алгоритмических предписаний и уметь действовать в соответствии с предложенным алгоритмом;
уметь самостоятельно ставить цели, выбирать и создавать алгоритм для решения учебных математических проблем;
уметь планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
в предметном направлении:
овладеть базовыми понятиями по основным разделам содержания; представлениями об основных изучаемых понятиях как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
уметь работать с математическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики;
развить представление о числе, овладеть навыками устных, письменных, инструментальных вычислений.
Ценностные ориентиры содержания курса
Математическое образование играет важную роль, как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная- с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения – от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использование современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможно стать образованным человеком.
В школе математика служит опорным предметом для изучения смежных дисциплин.
В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включается индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач – основной учебной деятельности на уроках алгебры - развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у учащихся точную, экономную, и информационную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры в 7-9 классахосновной школы отводится 315 ч из расчета 3 ч в неделю.
Рабочая программа для 9 класса рассчитана на 3 часа в неделю, всего 102 часа. Планирование учебного материала по алгебре рассчитано на 102 учебных часа согласно календарно-тематическому планированию на учебный год.
Изменения, внесенные в авторскую учебную программу и их обоснование:
В начале учебного года данной Рабочей программой предусмотрено повторение материала 8 класса в объёме 2 часа. В соответствии с планом внутри школьного контроля с целью изучения качества преподавания предметов, выносимых на итоговую аттестацию,добавлены две контрольные работы: входная контрольная работа (за курс алгебры 8 класса) и административная контрольная работа (за I полугодие), также запланирован пробный экзамен за курс основной школы в формате ОГЭ.В связи с этим, изменено соотношение часов на раздел «Повторение», и вместо предложенных в авторской программе 13 часов, в рабочей программе 11 часов. Количество контрольных работ 9.
Раздел 3. Содержание учебного предмета, курса.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса.
Содержание курса алгебры 9 класса включает следующие тематические блоки:
| № | Тема | Количество часов | Зачётные работы |
| 1 | Повторение материала 7-8 класса. | 2 |
|
| 2 | Неравенства. | 19 | 1 |
| 3 | Квадратичная функция. | 20 | 1 |
| 4 | Уравнения и системы уравнений. | 25 | 2 |
| 5 | Арифметическая и геометрическая прогрессии. | 17 | 1 |
| 6 | Статистика и вероятность. | 8 |
|
|
| Повторение. Решение задач по курсу алгебры 7-9 | 8 | 1 |
|
| Контрольные работы по тексту администрации: -входной контроль -промежуточный контроль -пробный ОГЭ |
|
1 1 1 |
|
| Итого | 102ч | 9 |
Отбор содержания обучения осуществляется на основе следующих дидактических принципов: соответствие обязательному минимуму содержания образования в основной школе; Усиление общекультурной направленности материала; учёт психолого-педагогических особенностей, актуальных для этого возрастного периода; создание условий для понимания и осознания воспринимаемого материала. В предлагаемом курсе алгебры выделяются следующие основные содержательные линии:
1.Неравенства.
Действительные числа как бесконечные десятичные дроби. Числовые неравенства и их свойства. Доказательство числовых иалгебраических неравенств. Линейные неравенства с одной переменной и их системы. Точность приближения, относительнаяточность.
Основная цель — познакомить учащихся со свойствами числовых неравенств и их применением к решению задач (сравнение и оценка значений выражений, доказательство неравенств и др.); выработать умение решать линейные неравенства с одной переменной и их системы.
Изучение темы начинается с обобщения и систематизации знаний о действительных числах, повторения известных учащимся терминов: натуральные, целые, рациональные, действительные числа — и рассмотрения отношений между соответствующими числовыми множествами.
Свойства числовых неравенств иллюстрируются геометрически и подтверждаются числовыми примерами. Рассмотрение вопроса о решении линейных неравенств с одной переменной сопровождается введением понятий равносильных уравнений и неравенств, формулируются свойства равносильности уравнений и неравенств. Приобретенные учащимися умения получают развитие при решении систем линейных неравенств с одной переменной. Рассматривается вопрос о доказательстве неравенств. Учащиеся знакомятся с некоторыми приемами доказательства неравенств; система упражнений содержит значительное число заданий на применение аппарата неравенств.
2.Квадратичная функция
Функция у = ах2 + bх + с и ее график. Свойства квадратичной функции: возрастание и убывание, сохранение знака на промежутке, наибольшее (наименьшее) значение. Решение неравенств второй степени с одной переменной.
Основная цель — познакомить учащихся с квадратичной функцией как с математической моделью, описывающей многие зависимости между реальными величинами; научить строить график квадратичной функции и читать по графику ее свойств сформировать умение использовать графические представлен для решения квадратных неравенств.
Изучение темы начинается с общего знакомства с функцией у =ах2 + bх + с; рассматриваются готовые графики квадратичных функций и анализируются их особенности (наличие оси симметрии, вершины, направление ветвей, расположение по отношению к оси х), при этом активизируются общие сведения о функциях, известные учащимся из курса 8 класса; учащиеся учатся строить параболу по точкам с опорой на ее симметрию. Далее следует более детальное изучение свойств квадратичной функции, особенностей ее графика и приемов его построения. В связи с этим рассматривается перенос вдоль осей координат произвольных графиков. Центральным моментом темы является доказательство того, что график любой квадратичной функции у = ах2 + bх + с может быть получен с помощью сдвигов вдоль координатных осей параболы у = ах2. Теперь учащиеся по коэффициентам квадратного трехчлена ах2+ bх + с могут представить общий вид соответствующей параболы и вычислить координаты ее вершины.
В системе упражнений значительное место должно отводиться задачам прикладного характера, которые решаются с опорой на графические представления.
3.Уравнения и системы уравнений
Рациональные выражения. Допустимые значения переменных, входящих в алгебраические выражения. Тождество, доказательство тождеств. Решение целых и дробных уравнений с одной переменной. Примеры решения нелинейных систем уравнений с двумя переменными. Решение текстовых задач. Графическая интерпретация решения уравнений и систем уравнений.
Основная цель — систематизировать сведения о рациональных выражениях и уравнениях; познакомить учащихся с некоторыми приемами решения уравнений высших степеней, обучить решению дробных уравнений, развить умение решать системы нелинейных уравнений с двумя переменными, а также текстовые задачи; познакомить с применением графиков для исследования и решения систем уравнений с двумя переменными и уравнений с одной переменной.
В данной теме систематизируются, обобщаются и развиваются теоретические представления и практические умения учащихся, связанные с рациональными выражениями, уравнениями, системами уравнений. Уточняется известное из курса 7 класса понятие тождественного равенства двух рациональных выражений; его содержание раскрывается с двух позиций — алгебраической и функциональной. Вводится понятие тождества, обсуждаются приемы доказательства тождеств.
Значительное место в теме отводится решению уравнений с одной переменной. Систематизируются и углубляют знания, учащихся о целых уравнениях, основное внимание уделяется решению уравнений третьей и четвертой степени уже знакомыми учащимся приемами — разложением на множители и введением новой переменной. Продолжается решение систем уравнений, в том числе рассматриваются системы, в которых одно уравнение первой, а другое — второй степени, и примеры более сложных систем.
В заключение проводится графическое исследование уравнений с одной переменной. Вообще графическая интерпретация алгебраических выражений, уравнений и систем должна широко использоваться при изложении материала всей темы.
4. Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии. Формулы n– гочлена и суммы nчленов арифметической и геометрической прогрессий. Простые и сложные проценты.
Основная цель — расширить представления, учащихся о числовых последовательностях; изучить свойства арифметической и геометрической прогрессий; развить умение решать задачи на проценты.
В данной теме вводятся необходимые термины и символика, в результате чего создается содержательная основа для осознанного изучения числовых последовательностей, которые неоднократно встречались в предыдущих темах курса. Введение понятий арифметической и геометрической прогрессий следует осуществлять на основе рассмотрения примеров из реальной жизни. На конкретных: примерах вводятся понятия простых и сложных процентов, которые позволяют рассмотреть большое число практико-ориентированных задач.
5. Статистические исследования
Генеральная совокупность и выборка. Ранжирование данных. Полигон частот. Интервальный ряд. Гистограмма. Выборочная дисперсия, среднее квадратичное отклонение.
Основная цель — сформировать представление о статистических исследованиях, обработке данных и интерпретации результатов.
В данной теме представлен завершающий фрагмент вероятностно-статистической линии курса. В ней рассматриваются доступные учащимся примеры комплексных статистических исследований, в которых используются полученные ранее знания о случайных экспериментах, способах представления данных и статистических характеристиках.
Характеристика основных видов деятельности ученика (на уровне учебных действий)
| Основное содержание по темам | Характеристика основных видов деятельности ученика (на уровне учебных действий) |
| Неравенства (19 ч) | |
| Действительные числа. Общие свойства неравенств. Решение линейных неравенств. Решение систем линейных неравенств. Доказательство неравенств. Что означают слова «с точностью до …». | Приводить примеры иррациональных чисел; распознавать рациональные и иррациональные числа; изображать числа точками координатной прямой. Находить десятичные приближения рациональных и иррациональных чисел; сравнивать и упорядочивать действительные числа. Описывать множество действительных чисел. Использовать в письменной математической речи обозначения и графические изображения числовых множеств, теоретико-множественную символику. Использовать разные формы записи приближённых значений; делать выводы о точности приближения по записи приближённого значения. Формулировать свойства числовых неравенств, иллюстрировать их на координатной прямой, доказывать алгебраически; применять свойства неравенств в ходе решения задач. Решать линейные неравенства, системы линейных неравенств с одной переменной. Доказывать неравенства, применяя приёмы, основанные на определении отношений «больше» и «меньше», свойствах неравенств, некоторых классических неравенствах. Распознавать на чертежах, рисунках, в окружающем мире геометрические фигуры. Приводить примеры аналогов в окружающем мире. Изображать геометрические фигуры и их конфигурации от руки и с использованием чертежных инструментов. Изображать геометрические фигуры на клетчатой бумаге. Измерять с помощью инструментов и сравнивать длины отрезков. Строить отрезки заданной длины с помощью линейки. Знать понятие координатного луча, единичного отрезка и координаты точки. Уметь начертить координатный луч и отметить на нем заданные числа, назвать число, соответствующее данному штриху на координатном луче. |
| Квадратичная функция (20 ч) | |
| Какую функцию называют квадратичной. График и свойства функции у=ах2. Сдвиг графика функции у=ах2 вдоль осей координат. График функции у=ах2 +bх+с. Квадратные неравенства. | Распознавать квадратичную функцию, приводить примеры квадратичных зависимостей из реальной жизни, физики, геометрии. Выявлять путём наблюдений и обобщать особенности графика квадратичной функции. Строить и изображать схематически графики квадратичных функций; выявлять свойства квадратичных функций по их графикам. Строить более сложные графики на основе графиков всех изученных функций. Проводить разнообразные исследования, связанные с квадратичной функцией и её графиком. Выполнять знаково-символические действия с использованием функциональной символики; строить речевые конструкции с использованием функциональной терминологии. Решать квадратные неравенства, а также неравенства, сводящиеся к ним, путём несложных преобразований; решать системы неравенств, в которых одно неравенство или оба являются квадратными. Применять аппарат неравенств при решении различных задач. |
| Уравнения и системы уравнений. (25ч) | |
| Рациональные выражения. Целые уравнения. Дробные уравнения. Системы уравнений с двумя переменными. Решение задач. Графическое исследование уравнений. | Распознавать рациональные и иррациональные выражения, классифицировать рациональные выражения. Находить область определения рационального выражения; доказывать тождества. Давать графическую интерпретацию функциональных свойств выражений с одной переменной. Распознавать целые и дробные уравнения. Решать целые и дробные выражения, применяя различные приёмы. Строить графики уравнений с двумя переменными. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Решать системы двух уравнений с двумя переменными, используя широкий набор приёмов. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путём составления уравнения или системы уравнений; решать составленное уравнение (систему уравнений); интерпретировать результат. Использовать функционально-графические представления для решения и исследования уравнений и систем. |
| Арифметическая и геометрическая прогрессии. (17 ч) | |
| Числовые последовательности. Арифметическая прогрессия. Сумма первых n членов арифметической прогрессии. Геометрическая прогрессия. Сумма первых nчленов геометрической прогрессии. Простые и сложные проценты. Сумма квадратов первых n натуральных чисел. | Применять индексные обозначения, строить речевые высказывания с использованием терминологии, связанной с понятием последовательности. Вычислять члены последовательностей, заданных формулой n-го члена или рекуррентной формулой. Устанавливать закономерность в построении последовательности, если выписаны первые несколько её членов. Изображать члены последовательности точками на координатной плоскости. Распознавать арифметическую и геометрическую прогрессии при разных способах задания. Выводить на основе доказательных рассуждений формулы общего члена арифметической и геометрической прогрессий, суммы первыхn членов арифметической и геометрической прогрессий; решать задачи с использованием этих формул. Рассматривать примеры из реальной жизни, иллюстрирующие изменения в арифметической прогрессии, в геометрической прогрессии; изображать соответствующие зависимости графически. Решать задачи на сложные проценты, в том числе задачи из реальной практики (с использованием калькулятора) |
| Статистика и вероятность. (8 ч) | |
| Выборочные исследования. Интервальный ряд. Гистограмма. Характеристики разброса. Статистическое оценивание и прогноз. | Осуществлять поиск статистической информации, рассматривать реальную статистическую информацию, организовывать и анализировать её (ранжировать данные, строить интервальные ряды, строить диаграммы, полигоны частот, гистограммы; вычислять различные средние, а также характеристики разброса). Прогнозировать частоту повторения события на основе имеющихся статистических данных. |
| Повторение. (8 ч) | |
Характеристики универсальных учебных действий,
осваиваемых в рамках изучаемого предмета:
Реализации программы способствует достижению следующих результатов:
в сфере личностных универсальных учебных действий у учащихся будут сформированы следующие качества:
независимость и критичность мышления;
воля и настойчивость в достижении цели.
Средством достижения этих результатов является:
– система заданий учебников;
– представленная в учебниках в явном виде организация материала по принципу минимакса;
– использование совокупности технологий, ориентированных на развитие самостоятельности и критичности мышления: технология системно- деятельностного подхода в обучении, технология оценивания.
в сфере регулятивных универсальных учебных действий учащиеся овладеют следующими типами учебных действий:
самостоятельно обнаруживать и формулировать учебную проблему, определять
цель учебной деятельности, выбирать тему проекта;
выдвигать версии решения проблемы, осознавать (и интерпретировать в случае
необходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;
составлять (индивидуально или в группе) план решения проблемы (выполнения
проекта);
работая по плану, сверять свои действия с целью и, при необходимости, исправлятьошибки самостоятельно (в том числе и корректировать план);
в диалоге с учителем совершенствовать самостоятельно выработанные критерии оценки.
Средством формирования регулятивных УУД служат технология системно- деятельностного подхода на этапе изучения нового материала и технология оценивания образовательных достижений (учебных успехов).
в сфере познавательных универсальных учебных действий учащиеся научаться:
преобразовывать модели с целью выявления общих законов, определяющих предметную область;
сопоставлять и отбирать информацию, полученную из разных источников;
передавать содержание в сжатом, выборочном или развёрнутом виде;
делать предложения об информации, которая нужна для решения учебной задачи;
строить логически обоснованное рассуждение, включающее установление причинно-следственных связей;
Средством формирования познавательных УУД служат учебный материал и прежде всего продуктивные задания учебника.
– Использование математических знаний для решения различных математических задач и оценки полученных результатов.
– Совокупность умений по использованию доказательной математической речи. – Совокупность умений по работе с информацией, в том числе и с различными математическими текстами.
– Умения использовать математические средства для изучения и описания реальных процессов и явлений.
– Независимость и критичность мышления.
– Воля и настойчивость в достижении цели.
в сфере коммуникативных универсальных учебных действий учащиеся научаться:
самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);
отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; – в дискуссии уметь выдвинуть контраргументы;
учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;
понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;
уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.
Средством формирования коммуникативных УУД служат технология проблемного обучения, организация работы в малых группах, также использование на уроках технологии личностно- ориентированного и системно - деятельностного обучения.
Предметными результатами изучения учебного предмета являются следующие умения:
-сравнивать и оценивать значение выражений, доказывать неравенства, знать свойства числовых неравенств и применять их при решении задач;
-знать понятие квадратичной функции, описывать её свойства, строить график квадратичной функции, по графику читать её свойства;
- вырабатывать умение решать квадратные неравенства, опираясь на графическое представление;
- находить область определения рациональных выражений;
-решать целые и дробные уравнения с одной переменной; решать системы уравнений с двумя переменными, содержащих одно уравнение первой, другое – второй степени;
-решать текстовые задачи с помощью уравнений и систем уравнений;
-вычислять сумму первых n членов арифметической и геометрической прогрессий; решать задачи на простые и сложные проценты.
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций (у=кх, где к
 0, у=кх+b, у=х2, у=х3, у =
0, у=кх+b, у=х2, у=х3, у =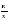 , у=
, у=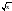 , у=ах2+bх+с, у= ах2+n, у= а (х- m)2), строить их графики;
, у=ах2+bх+с, у= ах2+n, у= а (х- m)2), строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
Элементы логики, КОМБИНАТОРИКИ, СТАТИСТИКИ и теории вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Раздел 4. Учебно-методическое и материально-техническое обеспечение.
Печатные пособия:
1. «Алгебра. Сборник рабочих программ 7 - 9 классы». Составитель Т. А. Бурмистрова. – – М.: Просвещение, 2011. – 96 с.
2. Дорофеев Г.В. Алгебра. 9 класс: учебник / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова. -М.: «Просвещение», 2016.
3. Видеман Т.Н. Поурочные планы. 9 класс. К учебному комплекту Г.В. Дорофеев (В помощь школьному учителю) –М.: Просвещение, 2009.
4.Макарычев Ю.Н. Дидактические материалы по алгебре для 9 класса. –М.: Просвещение,2010.
5. Гришина И.В. Математика. ГИА. Тренировочные работы. – Саратов: Лицей, 2014. – 64 с.
Технические средства обучения:
1) Компьютер.
2) Видеопроектор.
Интернет- ресурсы:
http://www.prosv.ru- сайт издательства «Просвещение» (рубрика «Математика»)
http:/www.drofa.ru - сайт издательства Дрофа (рубрика «Математика»)
http://festival.1september.ru/ - Я иду на урок математики (методические разработки)
http://pedsovet.su/load/18 - Уроки, конспекты.
http://vk.com/club91095222 - группа «Математика для всех» (для дистанционных консультаций учащихся)
http://www.center.fio.ru/som - методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.
http://www.edu.ru - Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента, сервер информационной поддержки Единого государственного экзамена.
http://www.internet-scool.ru- сайт Интернет – школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, включают подготовку сдачи ЕГЭ, ГИА.
http://www.legion.ru– сайт издательства «Легион»
http://www.intellectcentre.ru– сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений
http://www.fipi.ru- портал информационной поддержки мониторинга качества образования, здесь можно найти Федеральный банк тестовых заданий.
Контрольно-измерительный материал.
Контрольные (зачётные) работы составляются с учетом обязательных результатов обучения.
Тексты контрольных (зачётных) работ взяты из:
1.«Алгебра. Сборник рабочих программ 7 - 9 классы». Составитель Т. А. Бурмистрова. – М.: Просвещение, 2011. – 96 с.
2. Видеман Т.Н. Поурочные планы. 9 класс. К учебному комплекту Г.В. Дорофеев (В помощь школьному учителю) – М.: Просвещение, 2009.
Контрольные (зачётные) работы
Зачёт №1 «Неравенства»
| Отметка | «Зачёт» | «4» | «5» |
| Обязательная часть | 5 заданий | 5 заданий | 5 заданий |
| Дополнительная часть |
| 1 задание | 2 задания |
Вариант 1
Обязательная часть
1. Сравните числа: 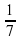 и 0,143… .
и 0,143… .
2. Оцените периметр прямоугольника со сторонами, а см и b см, если 7≤ а ≤ 8, 14 ≤ b≤ 15.
3. Решите неравенство 1 – (8 + х) ≥ 3х – 10 и изобразите множество его решений на координатной прямой.
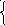
Решите систему неравенств (4 – 5):
4. х – 1
2х - 4
6. Запишите промежуток 20 ≤ х ≤ 24 в форме х = а ± h.
Дополнительная часть
7. Решите двойное неравенство х – 3
 8. Решите систему неравенств
8. Решите систему неравенств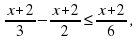
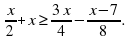
9. При каких значениях с уравнение 2х2 – 6х + с = 0 имеет два корня?
Вариант 2
Обязательная часть
1. Расположите в порядке возрастания: 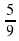 ; 0,54; 0,551… .
; 0,54; 0,551… .
2. Оцените площадь прямоугольника со сторонами х см и у см, если 9≤ х≤ 10, 15 ≤ у≤ 16.
3. Решите неравенство 2(х - 6) + 74х + 3 и изобразите множество его решений на координатной прямой.
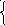
Решите систему неравенств (4 – 5):
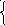
4. 3х + 4 ≥1, 5. 2х – 6
2х + 3≥ 7. x – 2
6. В рулоне содержится 57 м ткани с точностью до 0,5 м. Запишите это с помощью знака ± и с помощью двойного неравенства.
Дополнительная часть
7. Найдите все отрицательные решения неравенства 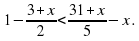
8. Решите систему неравенств
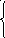 12 ≤ 6х,
12 ≤ 6х,
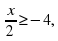
9 – 3х 0.
9. Не пользуясь калькулятором, сравните числа: 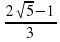 и
и 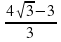
Зачёт №2 «Квадратичная функция»
| Отметка | «Зачёт» | «4» | «5» |
| Обязательная часть | 6 заданий | 6 заданий | 7 заданий |
| Дополнительная часть |
| 1 задание | 2 задания |
Каждый пункт, обозначенный буквой а или б, или в, считается как отдельное задание.
Вариант 1
Обязательная часть
1. С помощью графика (рис. 2.7 учебника) ответьте на вопросы:
а) Через сколько секунд после начала полёта ракеты достигла максимальной высоты?
б) Какое расстояние пролетела ракета за 3 с полёта?
2. Функция задана формулой у = 3х2 + 2х – 5.
а) Найдите значение функции при х=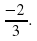
б) Найдите нули функции.
3. а) Постройте график функции у = -х2 + 4.
б) Укажите значения аргумента, при которых функцияпринимает отрицательные значения.
в) Укажите промежуток, на котором функция убывает.
4. Решите неравенство х2 – 3х + 2
Дополнительная часть
5. Запишите уравнение параболы, если известно, что она получена сдвигом параболы у = 2х2 вдоль оси х на четыре единицы вправо и вдоль оси у на две единицы вниз.
6. Найдите область определения функции 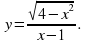
7. При каких значениях p и q вершина параболы у = х2 + pх + q находится в точке (-1; 5)?
Вариант 2
Обязательная часть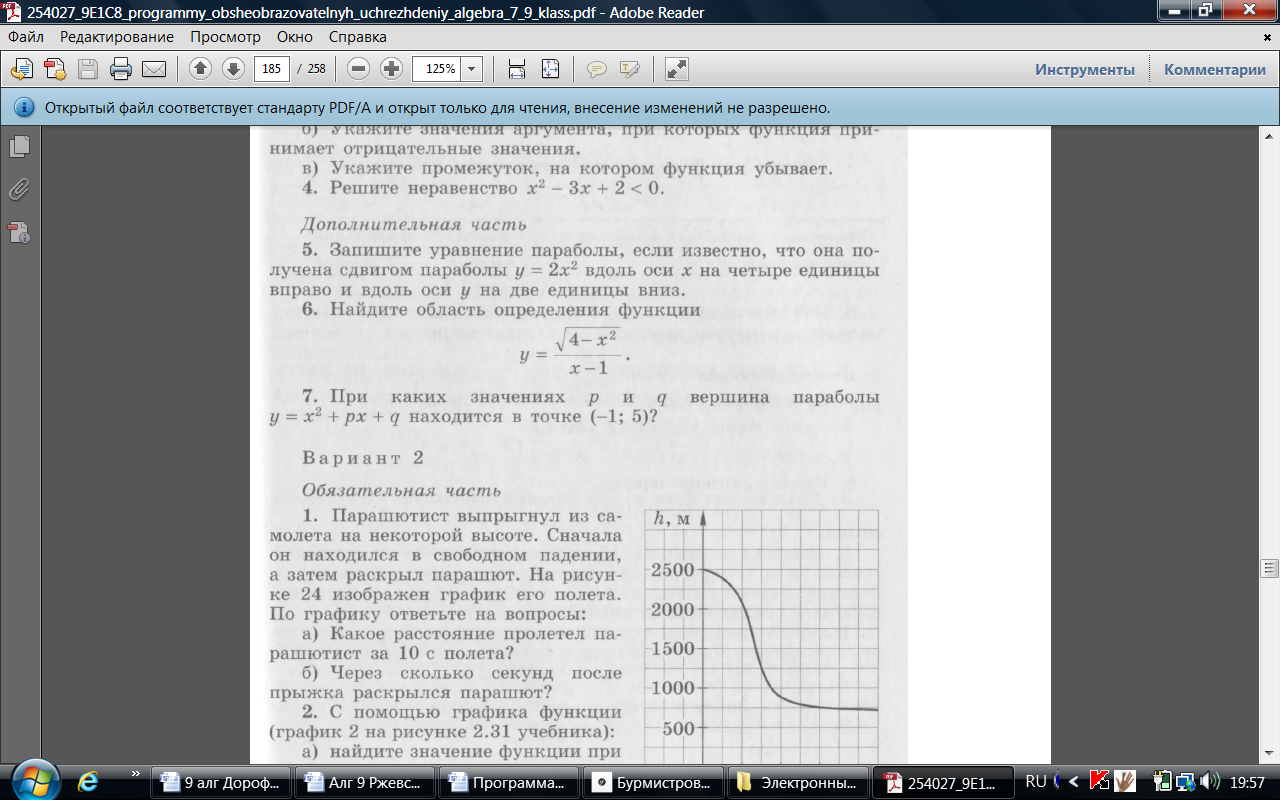
1. Парашютист выпрыгнул из самолёта на некоторой высоте. Сначала он находился в свободном падении, а затем раскрыл парашют. На рисунке изображён график его полёта. По графику ответьте на вопросы:
а) Какое расстояние пролетел парашютист за 10 с полёта?
б) Через сколько секунд после прыжка раскрылся парашют?
2. С помощью графика функции (график 2 на рис 2.31 учебника):
а) найдите значение функции при х = 3;
б) определите значение х, при которых функция принимает значение, равное -6.
3. а) Постройте график функции у = х2 + х – 6.
б) Укажите значение аргумента, при которых функция принимает положительные значения.
4. Решите неравенство х2 – 6х - 5
Дополнительная часть
5. Определите значения коэффициентов bи c, при которых вершина параболы у = 2х2 + bх + c находится в точке А (-1; 3).
6. Найдите область определения функции 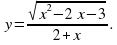
7. Найдите все целые значения m, при которых график функции у = 4х2 + mх + 1 расположен выше оси х.
Зачёт №3 «Рациональные выражения. Уравнения»
| Отметка | «Зачёт» | «4» | «5» |
| Обязательная часть | 4 заданий | 4 заданий | 5 заданий |
| Дополнительная часть |
| 1 задание | 2 задания |
Вариант 1
Обязательная часть
1.Упростить выражение 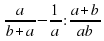 и найдите его значение при а = 0,2 и b= 0,3.
и найдите его значение при а = 0,2 и b= 0,3.
Найдите корни уравнения (2 – 3):
2. х(2х + 3)(2 – х) = 0 3. х + 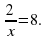
4. Укажите значения х, при которых выражение имеет смысл.
5. Бабушка прополола 15 грядок, после чего за прополку взялся внук и прополол 14 грядок. Всего они работали 5 ч. Сколько времени работал каждый, если за 1 ч бабушка пропалывала на 2 грядки меньше внука?
Выберите уравнение, соответствующее условию задачи, если через х обозначено количество грядок, пропалываемых внуком за 1 ч?
Дополнительная часть
8. Швея собиралась сшить 120 воротников к определённому сроку. Она подсчитала, что если будет в час шить на 2 воротника больше, чем наметила первоначально, то уже за 3 ч до срока сошьёт 136 воротников. Сколько воротников в час наметила шить швея первоначально?
Вариант 2
Обязательная часть
1.Упростить выражение 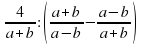 и найдите его значение при, а = 0,25 иb= 0,5.
и найдите его значение при, а = 0,25 иb= 0,5.
Найдите корни уравнения (2 – 3):
2. 2х3 – 8х = 0 3. 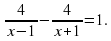
4. Укажите значения х, при которых выражение имеет смысл.
5. Машинистка должна напечатать 300 стр. Если она будет печатать в час на 1 стр. больше, чем обычно, то выполнит работу на 2 ч быстрее. С какой скоростью обычно печатает машинистка?
Выберите уравнение, соответствующее условию задачи, если буквой х обозначено количество страниц, которое обычно печатает машинистка за 1 ч?
А. Б.
В. 300(х + 1) – 300х = 2 Г.
Дополнительная часть
6. Решите уравнение 3х4 – 2х3 – 3х + 2 = 0.
7. Найдите область определения функции и постройте её график.
8. Одна уборочная машина работает в 3 раза быстрее, чем другая. Начав работу одновременно, они вместе могут заданный объём работы выполнить за 3 ч. За сколько часов каждая из машин, работая отдельно, может выполнить этот объём работы?
Зачёт №4 «Системы уравнений»
| Отметка | «Зачёт» | «4» | «5» |
| Обязательная часть | 3 заданий | 3 заданий | 4 заданий |
| Дополнительная часть |
| 1 задание | 2 задания |
Вариант 1
Обязательная часть
1. Решите систему уравнений х - у = 4,
х2 – 2у = 11.
2. Вычислите координаты точки пересечения графиков уравнений х2 + у2 = 5 и х – у = 1.
3. Гипотенуза прямоугольного треугольника равна 15 см, а один из катетов на 3 см меньше другого. Найдите катеты треугольника.
4. Выясните с помощью графиков, показанных на рисунке 3.22, а из учебника, сколько корней имеет уравнение х3 = Запишите его корни.
Дополнительная часть
5. Решите систему уравнений х – у = - 2,
6. Решите графически систему уравнений у = │х│,
у = 2х2 – 6.
7. Дорога между пунктами А и В состоит из двух участков: 24 км подъёма и 16 км спуска. Велосипедист преодолевает этот путь от А до В за 4 ч 20 мин, а обратный путь – 4 ч. Определите скорость велосипедиста на подъёме и на спуске.
Вариант 2
Обязательная часть
1. Решите систему уравнений ху = - 10,
х- у = 7.
2. Вычислите координаты точки пересечения графиков уравнений х2 - у2 =13 и х + у = -5.
3. Газон прямоугольной формы обнесён бордюром, длина которого 40 м. Площадь газона 96 м2. Найдите стороны газона.
4. Выясните с помощью графиков, показанных на рисунке 3.14, а из учебника, сколько корней имеет система уравнений х2 – у = 8,
у + х = - 2.
Запишите её решения.
Дополнительная часть
5. Решите систему уравнений х2 + у2 = 26,
ху = -5.
6. Решите графически уравнение х3 – 3х + 2 = 0.
7. Два велосипедиста выехали одновременно навстречу друг другу из пунктов А и В, расстояние между которыми 24 км, и встретились через 1 ч 20 мин. Первый прибыл в пункт В на 36 мин раньше, чем второй в пункт А. Найдите скорость каждого велосипедиста.
Зачёт №5 «Арифметическая и геометрическая прогрессия»
| Отметка | «Зачёт» | «4» | «5» |
| Обязательная часть | 4 заданий | 5 заданий | 5 заданий |
| Дополнительная часть |
| 1 задание | 2 задания |
Задания, отмеченные aи б, считаются как отдельные задания.
Вариант 1
Обязательная часть
1.Последовательность задана формулой n-го члена:
а) Запишите первые три члена этой последовательности и найдите
б) Является ли членом этой последовательности число 132?
2. Одна из двух данных последовательностей является арифметической прогрессией, другая – геометрической:
(): 12; 8; 4; …, (
): - 32; - 16; - 8; … .
а) Продолжите каждую из этих прогрессий, записав следующие её три члена.
б) Найдите двенадцатый член геометрической прогрессии.
3. Чтобы накопить денег на покупку велосипеда, Андрей в первую неделю отложил 10 р., а в каждую следующую откладывал на 5 р. больше, чем в предыдущую. Какая сумма будет у него через 10 недель?
Дополнительная часть
4. Найдите сумму всех двузначных чисел, кратных 3.
5. Сумма первых членов геометрической прогрессии равна - 40, знаменатель прогрессии равен -3. Найдите сумму первых восьми членов геометрической прогрессии.
6. Семья Петровых взяла кредит 25000 р. на покупку телевизора. Процентная ставка кредита равна 2% в месяц (проценты ежемесячно начисляются на всю сумму долга, включая начисленный в предыдущий месяц процент). Петровы выплатили весь кредит единовременно через полгода. Какую сумму они выплатили? Запишите выражение для вычисления этой суммы.
Вариант 2
Обязательная часть
1.Последовательность задана формулой n-го члена:
а) Запишите первые три члена этой последовательности и найдите
б) Какой номер имеет член этой последовательности, равный 110?
2. Одна из двух данных последовательностей является арифметической прогрессией, другая – геометрической:
(): 1; 2; 4; …, (
): - 15; - 12; - 9; … .
а) Продолжите каждую из этих прогрессий, записав следующие её три члена.
б) Найдите двадцатый член арифметической прогрессии.
3. Турист в первый день прошёл 20 км, а в каждый следующий – на 2 км меньше, чем в предыдущий. Какое расстояние прошёл турист за 7 дней?
Дополнительная часть
4. Сколько последовательных натуральных чисел, начиная с единицы, надо сложить, чтобы сумма превзошла 210?
5. Найдите сумму первых шести членов геометрической прогрессии, если её десятый член равен 64, а знаменатель равен
6. Автомобильный завод каждые два года снижает цену на определённую марку автомобиля на 20% по сравнению с её предыдущей ценой. В первый год выпуска новая модель стоила 40 000 р. Сколько будет стоить эта модель через 10 лет?
III Календарно-тематическое планирование по алгебре 9 класс (3 часа)
| Дата по плану | Дата по факту | № п/п | Тема урока | Виды учебной деятельности | Виды контроля |
|
|
| 1. | Повторение курса 7-8 кл. | Решение заданий с комментированием | ИРК |
|
|
| 2. | Повторение курса 7-8 кл. | Решение заданий с комментированием | ДРЗ |
|
|
| 3. | Диагностическая контрольная работа по тексту администрации | Индивидуальная работа |
|
| Глава I. Неравенства. (19 ч) | |||||
|
|
| 4. | Действительные числа. | Работа с учебником | ФО |
|
|
| 5. | Действительные числа. | Учебная практическая работа в парах | ФО, ОСР |
|
|
| 6. | Действительные числа. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 7. | Общие свойства неравенств. | Работа с учебником | ДРЗ |
|
|
| 8. | Общие свойства неравенств. | Индивидуальная работа с самооценкой. | СР |
|
|
| 9. | Решение линейных неравенств. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 10. | Решение линейных неравенств. | Решение примеров с комментированием | ФО, ОСР |
|
|
| 11. | Решение линейных неравенств. | Индивидуальная работа с самопроверкой | СР |
|
|
| 12. | Решение линейных неравенств. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 13. | Решение линейных неравенств. | Индивидуальная работа с самооценкой. | ИРК |
|
|
| 14. | Решение систем линейных неравенств. | Работа с учебником | ДРЗ |
|
|
| 15. | Решение систем линейных неравенств. | Практикум решения задач | СР |
|
|
| 16. | Решение систем линейных неравенств. | Практикум решения задач | ИДР |
|
|
| 17. | Доказательство неравенств. | Работа с учебником | ИДР |
|
|
| 18. | Доказательство неравенств. | Индивидуальная работа с самопроверкой | ДРЗ |
|
|
| 19. | Доказательство неравенств. | Индивидуальная работа с самооценкой. | СР |
|
|
| 20. | Что означают слова «с точностью до …» | Работа с учебником | ФО, ОСР |
|
|
| 21. | Что означают слова «с точностью до …» | Работа с учебником | ИКР |
|
|
| 22. | Зачёт №1 | Индивидуальная работа |
|
| Глава II. Квадратичная функция. (20 ч) | |||||
|
|
| 23. | Какую функцию называют квадратичной. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 24. | Какую функцию называют квадратичной. | Решение примеров с комментированием | ДРЗ |
|
|
| 25. | Какую функцию называют квадратичной. | Работа с учебником | ИРК |
|
|
| 26. | Какую функцию называют квадратичной. | Индивидуальная работа с самопроверкой | СР |
|
|
| 27. | График и свойства функции у = ах2 | Составление опорного конспекта | ФО, ОСР |
|
|
| 28. | График и свойства функции у = ах2 | Индивидуальная работа с самопроверкой | СР |
|
|
| 29. | Сдвиг графика функции у = ах2 вдоль осей координат. | Составление опорного конспекта | ФО, ОСР |
|
|
| 30. | Сдвиг графика функции у = ах2 вдоль осей координат. | Работа с учебником | ИРК |
|
|
| 31. | Сдвиг графика функции у = ах2 вдоль осей координат. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 32. | Сдвиг графика функции у = ах2 вдоль осей координат. | Решение примеров с комментированием | ДРЗ |
|
|
| 33. | Сдвиг графика функции у = ах2 вдоль осей координат. | Индивидуальная работа с самопроверкой | ИДР |
|
|
| 34. | График функции у = ах2 + bх + с. | Составление опорного конспекта | ФО, ОСР |
|
|
| 35. | График функции у = ах2 + bх + с. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 36. | График функции у = ах2 + bх + с. | Решение примеров с комментированием | ИРК |
|
|
| 37. | График функции у = ах2 + bх + с. | Индивидуальная работа с самопроверкой | ИДР |
|
|
| 38. | Квадратные неравенства. | Составление опорного конспекта | ФО, ОСР |
|
|
| 39. | Квадратные неравенства. | Практикум решения задач | ИРК |
|
|
| 40. | Квадратные неравенства. | Индивидуальная работа с самопроверкой | ДРЗ |
|
|
| 41. | Квадратные неравенства. | Практикум решения задач | ИДР |
|
|
| 42. | Зачёт №2 | Индивидуальная работа |
|
|
|
| 43. | Контрольная работа по тексту администрации. | Индивидуальная работа |
|
| Глава III. Уравнения и системы уравнений. (25 ч) | |||||
|
|
| 44. | 3.1 Рациональные выражения. | Работа с учебником | ДРЗ |
|
|
| 45. | 3.1 Рациональные выражения. | Решение примеров с комментированием | ИДР |
|
|
| 46. | 3.1 Рациональные выражения. | Индивидуальная работа с самопроверкой | СР |
|
|
| 47. | 3.1 Рациональные выражения. | Решение примеров с комментированием | ДРЗ |
|
|
| 48. | 3.2 Целые уравнения. | Работа с учебником | ФО, ОСР |
|
|
| 49. | 3.2 Целые уравнения. | Индивидуальная работа с самопроверкой | СР |
|
|
| 50. | 3.3 Дробные уравнения. | Работа с учебником | ДРЗ |
|
|
| 51. | 3.3 Дробные уравнения. | Решение примеров с комментированием | ИДР |
|
|
| 52. | 3.3 Дробные уравнения. | Практикум решения задач | ИРК |
|
|
| 53. | 3.3 Дробные уравнения. | Индивидуальная работа с самопроверкой | ПР |
|
|
| 54. | 3.4 Решение задач. | Работа с учебником | ДРЗ |
|
|
| 55. | 3.4 Решение задач. | Практикум решения задач | Т |
|
|
| 56. | 3.4 Решение задач. | Практикум решения задач | СР |
|
|
| 57. | 3.4 Решение задач. | Индивидуальная работа с самопроверкой | ИДР |
|
|
| 58. | 3.5 Системы уравнений с двумя переменными. | Составление опорного конспекта | ФО, ИДР |
|
|
| 59. | 3.5 Системы уравнений с двумя переменными. | Работа с учебником | ДРЗ |
|
|
| 60. | 3.5 Системы уравнений с двумя переменными. | Индивидуальная работа с самопроверкой | ФО, ОСР |
|
|
| 61. | 3.5 Системы уравнений с двумя переменными. | Практикум решения задач | ИРК |
|
|
| 62. | 3.6 Решение задач. | Решение примеров с комментированием | ФО, ИДР |
|
|
| 63. | 3.6 Решение задач. | Индивидуальная работа с самопроверкой | ПР |
|
|
| 63. | 3.7 Графическое исследование уравнений. | Составление опорного конспекта | ДРЗ |
|
|
| 65. | 3.7 Графическое исследование уравнений. | Решение примеров с комментированием | ИРК |
|
|
| 66. | 3.7 Графическое исследование уравнений. | Практикум решения задач | ПР |
|
|
| 67. | Зачёт №3 | Индивидуальная работа |
|
|
|
| 68. | Зачёт №4 | Индивидуальная работа |
|
| Глава IV. Арифметическая и геометрическая прогрессии. (17 ч) | |||||
|
|
| 69. | 4.1 Числовые последовательности. | Составление опорного конспекта | ФО, ИДР |
|
|
| 70. | 4.1 Числовые последовательности. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 71. | 4.2 Арифметическая прогрессия. | Работа с учебником | ДРЗ |
|
|
| 72. | 4.2 Арифметическая прогрессия. | Решение примеров с комментированием | ИРК |
|
|
| 73. | 4.2 Арифметическая прогрессия. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 74. | 4.3 Сумма первых n членов арифметической прогрессии. | Работа с учебником | ДРЗ |
|
|
| 75. | 4.3 Сумма первых n членов арифметической прогрессии. | Решение примеров с комментированием | ИДР |
|
|
| 76. | 4.3 Сумма первых n членов арифметической прогрессии. | Практикум решения задач | ПР |
|
|
| 77. | 4.4 Геометрическая прогрессия. | Работа с учебником | ДРЗ |
|
|
| 78. | 4.4 Геометрическая прогрессия. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 79. | 4.4 Геометрическая прогрессия. | Решение примеров с комментированием | ИДР |
|
|
| 80. | 4.5 Сумма первых n членов геометрической прогрессии. | Работа с учебником | ФО |
|
|
| 81. | 4.5 Сумма первых n членов геометрической прогрессии. | Практикум решения задач | ИРК |
|
|
| 82. | 4.6 Простые и сложные проценты. | Работа с учебником | ДРЗ |
|
|
| 83. | 4.6 Простые и сложные проценты. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 84. | 4.6 Простые и сложные проценты. | Практикум решения задач | ПР |
|
|
| 85. | Зачёт №5 | Индивидуальная работа |
|
| Глава V. Статистика и вероятность. (8 ч) | |||||
|
|
| 86. | 5.1 Выборочные исследования. | Работа с учебником | ДРЗ |
|
|
| 87. | 5.1 Выборочные исследования. | Учебная практическая работа в парах | ОСР |
|
|
| 88. | 5.2 Интервальный ряд. Гистограмма. | Составление опорного конспекта | ФО, ИДР |
|
|
| 89. | 5.2 Интервальный ряд. Гистограмма. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 90. | 5.3 Характеристики разброса. | Работа с учебником | ОСР |
|
|
| 91. | 5.3 Характеристики разброса. | Решение примеров с комментированием | ДРЗ |
|
|
| 92. | 5.4 Статистическое оценивание и прогноз. | Практикум решения задач | ПР |
|
|
| 93. | 5.4 Статистическое оценивание и прогноз. | Учебная практическая работа в парах | ФО, ИДР |
|
|
| 94. | Пробный экзамен. | Индивидуальная работа |
|
| Повторение. (8 ч) | |||||
|
|
| 95. | Повторение. Неравенства. | Практикум решения задач | СР |
|
|
| 96. | Повторение. Квадратичная функция. | Индивидуальная работа с самопроверкой | Т |
|
|
| 97. | Повторение. Уравнения и системы уравнений. | Индивидуальная работа с самопроверкой | Т |
|
|
| 98. | Повторение. Арифметическая и геометрическая прогрессии | Практикум решения задач | Т |
|
|
| 99. | Повторение. Статистика и вероятность. | Индивидуальная работа с самопроверкой | СР |
|
|
| 100. | Выполнение тестовых заданий в формате ОГЭ. | Индивидуальная работа с самопроверкой | Т |
|
|
| 101. | Выполнение тестовых заданий в формате ОГЭ. | Индивидуальная работа с самопроверкой | Т |
|
|
| 102. | Выполнение тестовых заданий в формате ОГЭ. | Индивидуальная работа с самопроверкой | Т |
ОСР – обучающая самостоятельная работа
ДРЗ – дифференцированное решение задач
ФО- фронтальный опрос
ИДР – индивидуальная работа у доски
ТЗ – творческое задание
ИРК – индивидуальная работа по карточкам
СР – самостоятельная работа
ПР – проверочная работа
Т – тестовая работа












