| «Согласовано» Руководитель МО Учителей предметников Пименова Н.А.______ Протокол №___ от «____ 20_____г.»
| «Согласовано» Заместитель директора по УВР _______ /Горшкова О.В./ «_____» ______20______г | «Утверждаю» Директор МОУ «СОШ им. Героя Советского Союза Н.Г.Маркелова с.Красная Звезда Ртищевского района Саратовской области» ______ /Крюкова Т.А./ Приказ № _________ от «_____» ______ 20_____ г. |
Рабочая программа
учебного предмета
«Математика»
основного общего образования
7 класс
Рассмотрено на заседании
педагогического совета
протокол № _____ от «____ « ____ 20____ г.
2022 – 2023 учебный год
Алгебра
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ УЧЕБНОГО ПРЕДМЕТА.
личностные:
1) ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
2) формирования коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
3) умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
4) первоначального представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
5) критичности мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
6) креативности мышления, инициативы, находчивости, активности при решении арифметических задач;
7) умения контролировать процесс и результат учебной математической деятельности;
8) формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
1) способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
2) умения осуществлять контроль по образцу и вносить необходимые коррективы;
3) способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
4) умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
5) умения создавать, применять и преобразовывать знаковосимволические средства, модели и схемы для решения учебных и познавательных задач;
6) развития способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
7) формирования учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
8) первоначального представления об идеях и о методах математики как об универсальном языке науки и техники;
9) развития способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
10) умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
11) умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
12) умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
13) понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
14) умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
15) способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
1) умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, ис-пользовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;
2) владения базовым понятийным аппаратом: иметь представление о числе, дроби, процентах, об основных геометрических объектах (точка, прямая, ломаная, угол, многоугольник, многогранник, круг, окружность, шар, сфера и пр.), формирования представлений о статистических закономерностях в реальном мире и различных способах их изучения;
3) умения выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
4) умения пользоваться изученными математическими формулами;
5) знания основных способов представления и анализа статистических данных; умения решать задачи с помощью перебора всех возможных вариантов;
6) умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА.
1. Выражения, тождества, уравнения.
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.
Основная цель - систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.
Первая тема курса 7 класса является связующим звеном между курсом математики 5—6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.
Нахождение значений числовых и буквенных выражений дает возможность повторить с учащимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.
В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки 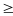 и
и 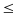 дается понятие о двойных неравенствах.
дается понятие о двойных неравенствах.
При рассмотрении преобразований выражений формально-оперативные умения остаются на том, же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.
Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия учащимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах = bпри различных значениях а и b. Продолжается работа по формированию у учащихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.
Изучение темы завершается ознакомлением учащихся с простейшими статистическими характеристиками: средним арифметическими, модой, медианой, размахом. Учащиеся должны уметь использовать эти характеристики для анализа ряда данных в несложных ситуациях.
2. Функции
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и ее график.
Основная цель - ознакомить учащихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.
Данная тема является начальным этапом в систематической функциональной подготовке учащихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у учащихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу.
Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида — прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у = kх, где k0, как зависит от значений kи bвзаимное расположение графиков двух функций вида у = kх + b
Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.
3. Степень с натуральным показателем
Степень с натуральным показателем и ее свойства. Одночлен. Функции у = х2, у = х3и их графики.
Основная цель — выработать умение выполнять действия над степенями с натуральными показателями.
В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора. Рассматриваются свойства степени с натуральным показателем. На примере доказательства свойств аm • аn = аm+n , аm : аn =аm-nгде mn, (аm)п = аmn, (аb)п = аnbnучащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений, содержащих степени, особое внимание следует обратить на порядок действий.
Рассмотрение функций у = х2, у = х3позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание учащихся на особенности графика функции у = х2 : график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.
Умение строить графики функций у = х2и у = х3используется для ознакомления учащихся с графическим способом решения уравнений.
4. Многочлены
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Основная цель — выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.
Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.
Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.
В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
5. Формулы сокращенного умножения .
Формулы (а ± b)2= а2 ± 2аb + b2, (а ± b)3= а3 ± 3а2Ь + Заb2 ± b3, (а ± b) (а2аb + b2) = а3 ± b3. Применение формул сокращенного умножения в преобразованиях выражений.
Основная цель — выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
В данной теме продолжается работа по формированию у учащихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b) (а + b) = а2 - Ь2, (а ± b)2= а2 + 2аb + b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».
Наряду с указанными рассматриваются также формулы (a ± b)3 = а3 ± За2b + Заb2 ± b3, а3 ± b3 = (а + b) (а2аb + b2). Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.
6. Системы линейных уравнений
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Основная цель - ознакомить учащихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.
Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.
Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.
Формируется умение строить график уравнения а + bу = с, где а 0 или Ь 0, при различных значениях а, b, с. Введение графических образов дает возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными.
Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.
7.Повторение
Календарно - тематическое планирование
| № урока п/п | Наименование разделов, тем | Сроки прохождения |
| План | Факт |
| 1 | Числовые выражения, содержащие знаки «+», «-» |
|
|
| 2 | Упрощение выражений. Числовые промежутки |
|
|
| 3 | Круг. Площадь круга |
|
|
| 4 | Входная контрольная работа |
|
|
| 5 | Анализ контрольной работы. Числовые выражения |
|
|
| 6 | Выражения с переменными. |
|
|
| 7 | Сравнения значений выражений |
|
|
| 8 | Свойства действий над числами |
|
|
| 9 | Тождества. |
|
|
| 10 | Тождественные преобразования выражений. |
|
|
| 11 | Контрольная работа № 1 «Преобразование выражений» |
|
|
| 12 | Анализ контрольной работы. Уравнения и его корни |
|
|
| 13 | Линейное уравнение с одной переменной |
|
|
| 14 | Линейное уравнение с одной переменной. |
|
|
| 15 | Решение задач с помощью уравнений |
|
|
| 16 | Решение задач с помощью уравнений |
|
|
| 17 | Решение задач с помощью уравнений |
|
|
| 18 | Среднее арифметическое
|
|
|
| 19 | Размах и мода |
|
|
| 20 | Медиана как статистическая характеристика |
|
|
| 21 | Медиана – срединное число |
|
|
| 22 | Контрольная работа № 2 по теме «Уравнения» |
|
|
| 23 | Анализ контрольной работы. Функции. |
|
|
| 24 | Вычисление значений функции по формуле |
|
|
| 25 | График функции |
|
|
| 26 | Построение графика функции по формуле |
|
|
| 27 | Прямая пропорциональность и её график |
|
|
| 28 | Прямая пропорциональность и её график |
|
|
| 29 | Линейная функция |
|
|
| 30 | Линейная функция и ее график |
|
|
| 31 | Взаимное расположение графиков линейных функций. |
|
|
| 32 | Задание функции несколькими формулами |
|
|
| 33 | Контрольная работа № 3 «Линейная функция» |
|
|
| 34 | Анализ контрольной работы. Определение степени с натуральным показателем |
|
|
| 35 | Определение степени с натуральным показателем |
|
|
| 36 | Умножение степеней |
|
|
| 37 | Деление степеней |
|
|
| 38 | Возведение в степень произведения и степени |
|
|
| 39 | Одночлен и его стандартный вид |
|
|
| 40 | Одночлен и его стандартный вид |
|
|
| 41 | Умножение одночленов |
|
|
| 42 | Возведение одночлена в степень |
|
|
| 43 | Функции у=х2, у=х3 и их графики |
|
|
| 44 | Контрольная работа № 4 «Степень с натуральным показателем» |
|
|
| 45 | Анализ контрольной работы. Многочлен и его стандартный вид |
|
|
| 46 | Сложение многочленов |
|
|
| 47 | Вычитание многочленов |
|
|
| 48 | Произведение одночлена и многочлена |
|
|
| 49 | Умножение одночлена на многочлен |
|
|
| 50 | Умножение одночлена на многочлен |
|
|
| 51 | Вынесение общего множителя за скобки |
|
|
| 52 | Разложение на множители многочлена |
|
|
| 53 | Решение уравнений |
|
|
| 54 | Контрольная работа № 5 «Действия с одночленами и многочленами» |
|
|
| 55 | Анализ контрольной работы. Произведение многочленов |
|
|
| 56 | Умножение многочлена на многочлен |
|
|
| 57 | Умножение многочлена на многочлен |
|
|
| 58 | Разложение многочлена на множители способом группировки |
|
|
| 59 | Разложение многочлена на множители способом группировки |
|
|
| 60 | Разложение многочлена на множители способом группировки |
|
|
| 61 | Контрольная работа № 6 «Действия с многочленами»
|
|
|
| 62 | Анализ контрольной работы. Возведение в квадрат суммы двух выражений |
|
|
| 63 | Возведение в квадрат разности двух выражений |
|
|
| 64 | Разложение на множители с помощью формул квадрата суммы и квадрата разности |
|
|
| 65 | Разложение на множители с помощью формул квадрата суммы |
|
|
| 66 | Разложение на множители с помощью формул квадрата разности |
|
|
| 67 | Умножение разности двух выражений на их сумму |
|
|
| 68 | Умножение разности двух выражений на их сумму |
|
|
| 69 | Умножение разности двух выражений на их сумму |
|
|
| 70 | Разложение разности квадратов на множители. |
|
|
| 71 | Разложение разности квадратов на множители. |
|
|
| 72 | Разложение разности квадратов на множители. |
|
|
| 73 | Сумма и разность кубов |
|
|
| 74 | Преобразование целых выражений |
|
|
| 75 | Преобразование целого выражения в многочлен |
|
|
| 76 | Применение различных способов для разложения на множители |
|
|
| 77 | Применение различных способов для разложения на множители |
|
|
| 78 | Применение преобразований целых выражений |
|
|
| 79 | Применение преобразований целых выражений |
|
|
| 80 | Контрольная работа № 7 «Преобразование выражений» |
|
|
| 81 | Анализ контрольной работы. Линейное уравнение с двумя переменными и их системы |
|
|
| 82 | Линейное уравнение с двумя переменными |
|
|
| 83 | График линейного уравнения с двумя переменными |
|
|
| 84 | График линейного уравнения с двумя переменными |
|
|
| 85 | Системы линейных уравнений с двумя переменными |
|
|
| 86 | Решение систем линейных уравнений |
|
|
| 87 | Способ подстановки |
|
|
| 88 | Способ подстановки |
|
|
| 89 | Способ сложения |
|
|
| 90 | Способ сложения |
|
|
| 91 | Способ сложения |
|
|
| 92 | Решение задач с помощью систем уравнений |
|
|
| 93 | Решение задач с помощью систем уравнений |
|
|
| 94 | Решение задач с помощью систем уравнений |
|
|
| 95 | Решение задач с помощью систем уравнений |
|
|
| 96 | Итоговая контрольная работа № 8 |
|
|
| 97 | Анализ контрольной работы. Выражения, тождества, уравнения |
|
|
| 98 | Формулы сокращенного умножения |
|
|
| 99 | Степень с натуральным показателем |
|
|
| 100 | Степень с натуральным показателем |
|
|
| 101 | Функции. |
|
|
| 102 | Системы линейных уравнений |
|
|
Геометрия
Планируемые результаты освоения учебного предмета на текущий учебный год
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
личностные:
формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов;
формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
формирование коммуникативной компетентности и общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициативу, находчивость, активность при решении геометрических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
регулятивные универсальные учебные действия:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
познавательные универсальные учебные действия:
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
формирование первоначальных представлений об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
коммуникативные универсальные учебные действия:
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;
умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов;
слушать партнера;
формулировать, аргументировать и отстаивать свое мнение;
предметные:
овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (геометрическая фигура, величина) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
овладение навыками устных письменных, инструментальных вычислений;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, умение применять систематические знания о них для решения геометрических и практических задач;
умение измерять длины отрезков, величины углов;
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочные материалы и технические средства.
Содержание учебного предмета
Основные свойства простейших геометрических фигур
Возникновение геометрии из практики. Начальные понятия планиметрии. Геометрические фигуры: точка, прямая, луч, плоскость. Отрезок, ломаная. Длина отрезка и его свойства. Угол. Виды углов: прямой, тупой, острый. Величина угла и ее свойства. Равенство отрезков, углов, треугольников.
Смежные и вертикальные углы
Смежные и вертикальные углы и их свойства. Биссектриса угла и её свойства. Параллельные прямые. Определения, доказательства, аксиомы и теоремы, следствия. Перпендикулярность прямых. Контрпример, доказательство от противного.
Признаки равенства треугольников
Треугольник, прямоугольные, остроугольные и тупоугольные треугольники. Признаки равенства треугольников: первый, второй, третий. Медиана, биссектриса и высота треугольника. Равнобедренный и равносторонний треугольники. Свойства и признаки равнобедренного треугольника. Прямая и обратная теоремы.
Основные задачи на построение с помощью циркуля и линейки
Сумма углов треугольника
Параллельные и пересекающиеся прямые. Основное свойство параллельных прямых. Признаки параллельности прямых. Сумма углов треугольника. Внешний угол треугольника.
Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная к прямой. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Свойство серединного перпендикуляра к отрезку.
Геометрические построения
Окружность и круг. Центр окружности, радиус, диаметр. Взаимное расположение прямой и окружности. Касательная и секущая к окружности, свойство касательной к окружности, равенство касательных, проведенных из одной точки. Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис. Окружность, описанная около треугольника. Окружность, вписанная в треугольник. Основные задачи на построение с помощью циркуля и линейки: построение треугольника по трём сторонам; угла, равного данному; биссектрисы угла; перпендикуляра к прямой, деление отрезка пополам. Понятие о геометрическом месте точек.
Повторение
Календарно - тематическое планирование
| № урока | Содержание учебного материала |
|
| Дата |
| план | факт |
| 1 | Геометрические фигуры. Точка и прямая. |
|
|
| 2 | Отрезок.
|
|
|
| 3 | Измерение отрезков |
|
|
| 4 | Полуплоскости. Полупрямая. |
|
|
| 5 | Угол. Прямые, острые и тупые углы.
|
|
|
| 6 | Биссектриса угла. |
|
|
| 7 | Откладывание отрезков
|
|
|
| 8 | Откладывание углов |
|
|
| 9 | Треугольник. Существование треугольника, равного данному. |
|
|
| 10 | Высота, биссектриса и медиана треугольника. |
|
|
| 11 | Существование треугольника, равного данному. |
|
|
| 12 | Параллельные прямые. |
|
|
| 13 | Теоремы и доказательства. Аксиомы. |
|
|
| 14 | Решение задач по теме «Основные свойства простейших геометрических фигур».
|
|
|
| 15 | Решение задач по теме «Основные свойства простейших геометрических фигур». |
|
|
| 16 | Контрольная работа №1 по теме «Основные свойства простейших геометрических фигур» |
|
|
| 17 | Анализ контрольной работы. Смежные углы.
|
|
|
| 18 | Свойство смежных углов. |
|
|
| 19 | Вертикальные углы |
|
|
| 20 | Свойство вертикальных углов. |
|
|
| 21 | Перпендикулярные прямые.
|
|
|
| 22 | Доказательство от противного. |
|
|
| 23 | Биссектриса угла. |
|
|
| 24 | Контрольная работа №2 по теме «Смежные и вертикальные углы» |
|
|
| 25 | Анализ контрольной работы. Первый признак равенства треугольников. |
|
|
| 26 | Использование аксиом при доказательстве теорем. |
|
|
| 27 | Второй признак равенства треугольников. |
|
|
| 28 | Закрепление. Второй признак равенства треугольников. |
|
|
| 29 | Равнобедренный треугольник. Обратная теорема.
|
|
|
| 30 | Обратная теорема. |
|
|
| 31 | Закрепление по темам: «равнобедренный треугольник.» «Обратная теорема.»
|
|
|
| 32 | Высота, биссектриса и медиана треугольника |
|
|
| 33 | Свойство медианы равнобедренного треугольника. |
|
|
| 34 | Свойство медианы равнобедренного треугольника. |
|
|
| 35 | Третий признак равенства треугольников. |
|
|
| 36 | Решение задач по теме «Признаки равенства треугольников».
|
|
|
| 37 | Контрольная работа №3 по теме « Признаки равенства треугольников» |
|
|
| 38 | Анализ контрольной работы. Закрепление по теме «Признаки равенства треугольников».
|
|
|
| 39 | Параллельность прямых. |
|
|
| 40 | Углы, образованные при пересечении двух прямых секущей. |
|
|
| 41 | Признак параллельности прямых. |
|
|
| 42 | Свойство углов, образованных при пересечении параллельных прямых секущей. |
|
|
| 43 | Свойство углов, образованных при пересечении параллельных прямых секущей. |
|
|
| 44 | Сумма углов треугольника. |
|
|
| 45 | Сумма углов треугольника. |
|
|
| 46 | Внешние углы треугольника. |
|
|
| 47 | Прямоугольный треугольник. |
|
|
| 48 | Существование и единственность перпендикуляра к прямой. |
|
|
| 49 | Решение задач по теме «Сумма углов треугольника». |
|
|
| 50 | Контрольная работа №4 по теме «Сумма углов треугольника» |
|
|
| 51 | Анализ контрольной работы. Окружность. |
|
|
| 52 | Окружность, описанная около треугольника. |
|
|
| 53 | Касательная к окружности. |
|
|
| 54 | Окружность, вписанная в треугольник. |
|
|
| 55 | Что такое задачи на построение.. |
|
|
| 56 | Построение треугольника с данными сторонами |
|
|
| 57 | Построение угла, равного данному. Построение биссектрисы угла |
|
|
| 58 | Деление отрезка пополам. Построение перпендикулярной прямой. |
|
|
| 59 | Итоговая контрольная работа |
|
|
| 60 | Анализ контрольной работы. Геометрическое место точек. Метод геометрических мест. |
|
|
| 61 | Повторение курса геометрии 7 класса. Решение задач. |
|
|
| 62 | Сумма углов треугольников. |
|
|
| 63 | Высота, биссектриса и медиана треугольника. |
|
|
| 64 | Смежные и вертикальные углы. |
|
|
| 65 | Признаки равенства треугольников |
|
|
| 66 | Внешние углы треугольника. Прямоугольный треугольник |
|
|
| 67 | Окружность, описанная около треугольника |
|
|
| 68 | Окружность, описанная около треугольника |
|
|
















