Министерство Образования и Науки Российской Федерации
Муниципальное общеобразовательное бюджетное учреждение
«Средняя общеобразовательная школа № 12»
| Полное название темы работы | Приемы устного быстрого счета |
| Тип работы | исследовательская работа
|
| Фамилия имя автора | Зонов Константин |
| Домашний адрес автора | город Минусинск, улица ……, дом ….., квартира …., индекс 662610 |
| Место учебы: | Муниципальное общеобразовательное бюджетное учреждение «Средняя общеобразовательная школа № 12» |
| Класс | 6 |
| Руководитель | Глебов Алексей Юрьевич, «МОБУ СОШ № 12», учитель математики и информатики, контактный телефон: +7 9233176757 |
| e-mail (обязательно)
Контактный телефон | Ваш ящик написать и телефон. руководитель работы: zahage@mail.ru
|
Минусинск 2014
АННОТАЦИЯ
Зонов Константин
г. Минусинск, МОБУ «СОШ № 12», 6 класс
«Приемы устного быстрого счета»
руководитель: Глебов Алексей Юрьевич, МОБУ «СОШ № 12», учитель математики и информатики.
Работа состоит из двух частей: теоретическая часть (глава 1 и 2), где собраны основные сведения о людях обладающими феноменальными вычислительными способностями, а также сами методы быстрого устного счета, и практическая часть, где приведены результаты опытно-экспериментальной работа. В приложении собран материал для тренинга.
Цель работы: доказать результативность использования различных видов устного счета для увеличения вычислительных навыков.
Методы исследования:
Анализ литературы;
Наблюдение;
Диагностика;
Сравнительный анализ.
В результате исследования были получены следующие результаты:
-
с помощью приемов быстрого устного счета можно улучшить вычислительные навыки школьников, независимо от их феноменальных математических способностей.
-
Знание приемов быстрого счета позволяет упрощать вычисления, развивает логическое мышление и гибкость ума, экономит время на самостоятельных и контрольных работах;
-
Представленные приемы быстрого устного счета, могут быть использованы учителями для развития вычислительных навыков у учащихся 5- 6 классах.
Содержание АННОТАЦИЯ Введение 5
Глава 1. О ФЕНОМЕНАЛЬНЫХ СПОСОБНОСТЯХ ЛЮДЕЙ-СЧЕТЧИКОВ 7
Глава 2. Способы быстрого устного счета 12
2.1 Способы быстрого сложения чисел 12
Поразрядное сложение чисел………………………………………………………... 12
Прибавление к одному числу отдельных разрядов другого числа, всегда начиная с высших………………………………………………………………………………... 12
Сложение путем округления………………………………………………………... 12
Сложение с использованием свойств действий с числами……………………….. 12
Сложение десятичных дробей, путем поразрядного сложения, начиная с высших разрядов………………………………………………………………………………. 12
2. 2 Способы быстрого вычитания чисел 13
Поразрядное вычитание……………………………………………………………… 13
Вычитание с использованием свойств действий с числами………………………..13
Вычитание путем уравнивания числа единиц последних разрядов уменьшаемого.13
Вычитание путем округления уменьшаемого или вычитаемого или одновременно обоих…………………………………………………………………………………… 13
2.3 Способы быстрого умножения чисел .13
Умножение на 4, 8,16 и т.д………………………………………………………….... 13
Умножение на 5, 50, 0,5………………………………………………………………..13
Умножение на 25, 2,5, 0,25…………………………………………………………… 14
Умножение на 125, 12,5, 1,25, 0,125…………………………………………………. 14
Умножение на 1,5 и на 15…………………………………………………………….. 14
Умножение на 11……………………………………………………………………… 14
Умножение двузначного числа на 101 и на 10101………………………………….. 15
Умножение на 9, 99 и 999……………………………………………………………...13
Применение распределительного закона умножения относительно сложения и вычитания ко множителям, один из которых представлен в виде суммы или разности………………………………………………………………………………... 14
2.4 Способы быстрого деления чисел ..15
Последовательное деление…………………………………………………………… 15
Деление на 0,5, 5, 50 и 500……………………………………………………………. 16
Деление на 25, 2,5, 0,25………………………………………………………………. 16
Деление на 125, 12,5, 1,25, 0,125……………………………………………………... 16
2.5 Без карандаша и бумаги 16
ГЛАВА 3. ДИАГНОСТИКА ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ 19
ЗАКЛЮЧЕНИЕ 21
список используемой литературы 22
ПРИЛОЖЕНИЕ 1 «ЧУДО СЧЕТЧИКИ» 23
ПРИЛОЖЕНИЕ 2 «МАТЕРИАЛ ДЛЯ ТРЕНИНГА» 25
ВВЕДЕНИЯ
Актуальность. В наш век, век новых технологий и развития компьютерной техники, разговор об устном счете может показаться неуместным, однако и по сей день гибкость ума является предметом гордости людей, а способность, производить в уме вычисления вызывает откровенное удивление.
Во все времена математика была и остается одним из основных предметов в школе, потому что математические знания необходимы всем людям. Не каждый школьник, обучаясь в школе, знает, какую профессию он выберет в будущем, но каждый понимает, что математика необходима для решения многих жизненных задач: расчеты в магазине, оплата за коммунальные услуги, расчет семейного бюджета и т.д. Кроме того, всем школьникам необходимо сдавать экзамены в 9-м классе и в 11-м классе, а для этого, обучаясь с 1-го класса, необходимо качественно осваивать математику и прежде всего, нужно научиться считать.
Сегодня все чаще на помощь ученикам приходят калькуляторы, и все большее количество учеников не может считать устно. А ведь изучение математики развивает логическое мышление, память, гибкость ума, приучает человека к точности, к умению видеть главное, сообщает необходимые сведения для понимания сложных задач, возникающих в различных областях деятельности современного человека. Поэтому в своей работе я хочу показать, как можно считать быстро и правильно и что процесс выполнения действий может быть не только полезным, но и интересным занятием.
Тема «Приемы устного быстрого счета».
В данной работе мы рассмотрим некоторые способы быстрых вычислений, которые могут пригодиться на уроках математики в школе и не только.
Структура работы:
-
введение;
-
теоретическая часть, которая включает в себя сведения о людях, обладающих феноменальными способностями в области устного счета и подбора задач на эту тему, основные приемы быстрого устного счета;
-
практическая, которая демонстрирует эксперимент по изучению приемов устного счета;
-
заключение,
-
использованная литература;
-
приложение.
Цель работы: доказать результативность использования различных видов устного счета для улучшения вычислительных навыков.
Объект исследования: приемы быстрого устного счета.
Предмет исследования: эффективность приемов быстрого устного счета у школьников.
Гипотеза исследования: с помощью приемов быстрого устного счета можно улучшить вычислительные навыки школьников, независимо от их феноменальных математических способностей.
Для достижения цели работы и подтверждения гипотезы я поставил следующие задачи:
-
Изучение способов быстрого устного счета.
-
Подбор материалов для тренинга.
-
Проведение диагностики, изучение результатов исследования.
-
Сделать выводы, по использованию данных видов устных упражнений.
-
Сведения о людях, которые имеют феноменальные способности быстрого счета.
Методы исследования:
Теоретическая значимость работы: сделан анализ и произведено обобщение теоретического и практического материала.
Практическая значимость: работа представляет интерес как для нас школьников, так и для родителей и для учителей. Подготовлены рекомендации. Презентация может быть использована на уроках обществознания в восьмых классах, а также на классных часах в школе.
ГЛАВА I. «О ФЕНОМЕНАЛЬНЫХ СПОСОБНОСТЯХ ЛЮДЕЙ-СЧЕТЧИКОВ»
Иногда встречаются лица с феноменальной способностью производить в уме математические действия буквально с астрономическими числами, рассчитывать день недели любого, сколь угодного далекого года, запоминать в прямой и обратной последовательности большое количество слов и цифр. В соответствующей обстановке это производит сильное эмоциональное воздействие на зрителей. Очевидцы рассказывают, что И.В.Курчатов – научный руководитель проекта по созданию первого советского атомного оружия – легко обходился без таблицы десятичных логарифмов, поскольку многие значения из нее помнил на память. Шахматисты высокого уровня довольно успешно играют вслепую на многих досках одновременно. Этим отличался, в частности, известный любителям шахмат знаменитый гроссмейстер М. Таль. Здесь имеет место благоприятное сочетание прирожденных особенностей мозга с длительной тренировкой.
Принципиально важно, что, несмотря на внешне трюковое проявление, реальность феномена быстрого счета оценивается по абсолютным показателям, проверка обмана достигается объективными приемами, а сами счетчики для демонстрации своих способностей, как правило, не предъявляют требований к созданию каких-то особых условий, кроме, пожалуй, тишины.
Ни одна из возможностей нашего мозга не кажется столь удивительной, как загадка чудо-счетчиков.
...В зрительном зале погас свет. На сцену, ярко освещенную огнями рампы, вышел человек в строгом черном костюме - не цирковой артист, не конферансье, не исполнитель популярных песенок. У него в руках мел и тряпка. Они как-то непривычны на сцене.
Эстрадный номер начинается.
- Назовите мне, пожалуйста, – обращается артист к зрителям, – многозначное множимое и многозначный множитель, и прошу вас найти вместе со мной их произведение.
- Один миллион пятьсот девяносто четыре тысячи триста двадцать три умножьте на три тысячи четыреста пятьдесят шесть, – просят из зала.
Проходит несколько секунд, и все читают на доске результат - 5 509 980 288.
Артист терпеливо ждет, пока зрители перемножат на бумаге числа. После этого он называет также все промежуточные результаты, полученные при умножении (см. Приложение 1, Вильям Клайн, человека-компьютер). [9]
Что же собой представляет это дарование? Никакое описание, никакой рассказ не могут дать о нем полного представления. Нужно присутствовать при живой демонстрации, чтобы понять, до какой степени справедлив эпитет «чудо».
Вот рассказ об эксперименте, проведенном одним из исследователей с мадемуазель Осака. Испытуемую просили возвести в квадрат 97, получить десятую степень того же числа. Она делала это моментально. Затем предлагали извлечь корень шестой степени из 40 242 074 782 776 576. Она отвечала тотчас и без ошибок.
В 1927 году доктор Ости и математик Сент-Лаге экзаменовали слепого счетчика Луи Флери. Среди поставленных задач была следующая: дается число, нужно разложить его на куб некоторого числа и четырехзначное число.
Флери предложили число 707 358 209. Он размышлял 28 секунд и дал решение: 891 в кубе и 5236. Ему предложили 211717440. Ответ последовал через 25 секунд: 596 в кубе и 8704. [9]
В Ванском районе Западной Грузия живет Арон Чиквашвили. (см. Приложение 1, Арон Чиквашвили) Он свободно манипулирует в уме многозначными числами. «Счетный механизм» Чиквашвилй не знает усталости и ошибок.
Как-то друзья решили проверить возможности чудо-счетчика. Задание было суровым: сколько слов и букв скажет диктор, комментирующий второй тайм футбольного матча «Спартак» (Москва) – «Динамо» (Тбилиси). Одновременно был включен магнитофон. Ответ последовал, как только диктор сказал последнее слово: 17 427 букв, 1835 слов. На проверку ушло... пять часов. Ответ оказался правильным. [9]
39-летний Арон Чиквашвилй окончил юридический и экономический факультеты вуза.
Среди чудо-счетчиков особенно большой популярностью пользуются задачи, в основе которых лежит календарное исчисление. Проносясь мысленно через века и тысячелетия, преодолевая трудности недесятичных соотношений (ведь неделя состоит из 7 дней, сутки из 24 часов, час из 60 минут и т. д.), они, за несколько секунд способны проделать сотни операций и сообщить, что 1 января 180 года была пятница. И все это делается с учетом високосных лет, смены календаря в 1582 году и т. д. Они, например, могут сказать, сколько секунд прошло со времени смерти Нерона до падения Константинополя. Однажды за беседой два счетчика Иноди и Дагбер, шутя, задавали друг другу вопросы такого рода: какой день недели будет 13 октября 28448723 года? [9]
Некоторые задачи, которые люди-счетчики решают как бы шутя, всего за несколько секунд, по мнению математиков, потребовали бы многих месяцев обычного счета. После этого пришлось бы в течение длительного времени проверять полученные результаты или же прибегнуть к помощи электронной машины.
Какими же методами оперируют чудо-счетчики? Приходит ли «дар» с детства, в юности или приобретается, воспитывается в течение жизни?
Пытались объяснить эту способность исключительной памятью, тем, что психологи называют «гипермнезией». Конечно, до какой-то степени мы сталкиваемся здесь с проявлением поистине чудовищной памяти, но одной памятью не объяснить существа явления. [9]
Рассказывают, что отец Гаусса обычно платил своим рабочим в конце недели, прибавляя к каждодневному заработку плату за сверхурочные часы. Однажды, после того как Гаусс-отец закончил расчеты, следивший за операциями отца ребенок, которому было едва три года, воскликнул:
- Папа, подсчет неверен! Вот какая должна быть сумма.
Вычисления повторили и с удивлением убедились, что малыш указал правильную сумму.
Несколько лет назад газеты сообщали о юном математическом феномене Бориславе Гаджански.
- Можешь ли ты, Борислав, извлечь корень двадцать второй степени из числа 348 517 368 454 361 458 872?
Мальчик на минуту задумывается: «Восемь».
- А теперь извлеки корень тридцать первой степени из числа 538 436 517 832 435 456 582.
Еще минута на размышление.
- Четыре.
В свои одиннадцать лет Борислав Гаджански из югославского города Зренянине отлично знал высшую математику в объеме программы вуза и без помощи карандаша и бумаги производил сложнейшие математические расчеты. [9]
Проявляется ли этот дар очень рано или очень поздно, его появление всегда стихийно. Происходит молниеносное превращение. Обладатель дара иногда бывает «отсталым» во всех других областях, но среди цифр он чувствует себя как дома и быстро достигает фантастической виртуозности.
Что же происходит с чудо – счетчиком дальше?
Обычно их умение бесконечно совершенствуется вплоть до глубокой старости. Но бывает и так, что мало-помалу оно исчезает, по мере того как его обладатель получает обычное для всех детей образование. Например, Ампер стал одним из крупнейших ученых, но он потерял способность, к устному счету, по мере того как расширялись его познания в области классической математики. Наоборот, Гаусс и Эйлер соединяли вплоть до смерти обе стороны своей гениальности.
Интересно, что многие люди-счетчики не имели вообще никакого понятия, так они считают: «Считаем, и все! А как считаем, бог его знает». Такие ответы не удивительны. Некоторые из счетчиков были совсем необразованными, людьми. Англичанин Бакстон, счетчик-виртуоз, так никогда и не научился читать, не знал цифр. Американский негр счетчик Томас Фулер умер неграмотным в возрасте 80 лет. [9]
Такие люди всегда очень интересовали психологов и математиков, которые старались выяснить, в чем секрет их способностей. Но объяснения, которые чудо - счетчики давали, пытаясь раскрыть свое умение, на первый взгляд казались странными, и даже очень.
Например, Урания Диамонди говорила - владеть цифрами ей помогает их цвет: 0 - белый, 1 - черный, 2 - желтый, 3 - алый, 4 - коричневый, 5 - синий, 6 - темно-желтый, 7 -ультрамарин 8 - серо-голубой, 9 - темно-бурый. Процесс вычисления представлялся ей в виде бесконечных симфоний цвета.
Монде и Кальбюрн ясно видели, как перед их глазами выстраиваются ряды цифр, начертанные чьей-то невидимой рукой. Их «прием» заключался в том, чтобы прочесть эту «волшебную» запись. Брат Урании, Перриклес Диамонди, говорил: «Цифры как бы скапливаются у меня в черепной коробке».
Очень «прост» метод Иноди. Ему казалось, будто вместо него считает чей-то голос, и, пока этот внутренний голос производит вычисления, сам он либо продолжает разговаривать, либо наигрывает на флейте. Морис Дагбер производит головокружительные вычисления, играя на скрипке.
Некоторое время назад во Франции, в Лилле, в присутствии авторитетного жюри из физиков, инженеров, кибернетиков, математиков и психологов Морис Дагбер вступил в спор с электронной выделительной машиной, производящей около миллиона операций в секунду.
Дагбер заявил, что признает себя побежденным лишь в том случае, если машина решит семь задач раньше, чем он десять...
Дагбер решил все 10 задач за 3 минуты 43 секунды, а электронная машина только за 5 минут 18 секунд! [9]
Подобные соревнования дело непростое. В одном из подобных состязаний участвовали молодой счетчик-феномен Игорь Шелушков и электронная вычислительная машина «Мир».
Надо отдать должное таланту Шелушкова. Он блестяще выиграл соревнование, как и Дагбер во Франции.
В Сиднейском университете в Индии тоже проходили соревнования человека и машины. Шакунтала Деви тоже опередила несколько вычислительных машин.Она помогла индийским банкам выверить и свести миллиардные балансы, провела огромные расчеты, которые помогут при решении сложной для Индии демографической проблемы.
Некоторые чудо – счетчики подвергались научному обследованию. Иноди однажды был приглашен на заседание Французской академий наук. Отчет о заседании был дан математиком Дарбу. Ученые пришли к выводу, что Иноди использует некоторые классические приемы, которые он сам «переоткрыл». Одна из комиссий при академии, в которую, в частности, входили известные ученые Араго, Коши, исследовала Анри Монде. По свидетельству Коши, полуграмотный сын дровосека Монде применял бином Ньютона. К подобным выводам пришла академия и при эксперименте в 1948 году с Морисом Дагбером. [9]
Ученые считают, что дар феноменального счета в том виде, в каком он наблюдается у взрослых счетчиков, является в какой-то степени даром «воспитанным» (то есть приобретенным в результате систематических упражнений). Бродя по джунглям чисел, люди-счетчики зачастую находят приемы, которые дают им возможность сокращать вычисления.
Пожалуй, единственная научно-обоснованная и достаточно подробно разработанная система резкого повышения быстроты устного счета создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием «Системы быстрого счета».
История ее создания необычная. В 1941 году гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счета. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность. Система Трахтенберга позволяет резко ускорить процесс выполнения операций умножения, деления, сложения, возведения в степень и извлечения корня. [9]
Как мы видим, быстрый счет это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит, ее можно изучать, ей можно следовать, ею можно овладеть.
ГЛАВА 2. СПОСОБЫ БЫСТРОГО УСТНОГО СЧЕТА
2.1 Способы быстрого сложения чисел
Поразрядное сложение чисел
К разрядам первого слагаемого прибавляют разряды второго слагаемого, начиная с высших (сотни, десятки и т.д.):
Прибавление к одному числу отдельных разрядов другого числа, всегда начиная с высших
К разрядам первого слагаемого прибавляют разряды другого слагаемого:
Сложение путем округления
Если слагаемые близки к круглым числам, то их заменяют разностью или суммой между круглым числом и дополнением:
=7000–95=6905.
Сложение с использованием свойств действий с числами
Слагаемые разбивают на такие группы, которые в сумме дают круглые числа:
Если одно слагаемое близко к круглому числу, то его заменяют разностью и дополнением между круглым числом:
Если оба слагаемых близки к круглому числу, то они заменяются разностью между круглым числом и дополнением:
Сложение десятичных дробей, путем поразрядного сложения, начиная с высших разрядов
Отдельно сложить целые части, десятичные доли, а затем сложить полученные результаты:
-
8,4+6,51=((8,4+6)+0,5)+0,01=(14,4+0,5)+0,01=14,9+0,01=14,91.
2.2 Способы быстрого вычитания чисел
Поразрядное вычитание
Если число единиц какого-либо разряда вычитаемого больше числа единиц того же разряда уменьшаемого, то последнее число единиц увеличивается на 10 путем заимствования одной единицы следующего высшего разряда уменьшаемого:
Вычитание с использованием свойств действий с числами
Вычитание путем уравнивания числа единиц последних разрядов уменьшаемого
Вычитание путем округления уменьшаемого или вычитаемого или одновременно обоих
Если уменьшаемое и/или вычитаемое близки к круглому числу, то их заменяют разностью или суммой между круглым числом и дополнением:
2.3 Способы быстрого умножения чисел
Умножение на 4, 8,16 и т.д.
Чтобы число умножить на 4, 8, 16 его последовательно удваивают:
Умножение на 5, 50, 0,5
Чтобы умножить число на 5, нужно умножить его на 10 и разделить на 2:
Чтобы умножить число на 50, нужно умножить его на 100 и полученное произведение разделить на 2:
Чтобы умножить число на 0,5, нужно разделить на 2:
Умножение на 25, 2,5, 0,25
Чтобы умножить число на 25, нужно умножить его на 100 и полученное произведение разделить на 4:
Чтобы умножить число на 2,5, нужно умножить его на 10 и полученное произведение разделить на 4:
Чтобы умножить число на 0,25, нужно разделить его на 4:
Умножение на 125, 12,5, 1,25, 0,125
Чтобы умножить число на 125, нужно умножить его на 1000 и разделить на 8:
Чтобы умножить число на 12,5, нужно умножить его на 100 и разделить на 8:
Чтобы умножить число на 1,25, нужно умножить его на 10 и разделить на 8:
Чтобы умножить число на 0,125, нужно разделить его на 8.
Умножение на 1,5 и на 15
Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину:
Чтобы умножить число на 15, нужно исходное число умножить на 10 и прибавить половину полученного произведения:
Умножение на 11
1 способ. Чтобы число умножить на 11 , к нему приписывают ноль и прибавляют исходное число:
2 способ. Следует “раздвинуть” цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд:
-
34*11=374, т.к. 3+4=7, семерку помещаем между тройкой и четверкой,
-
68*11=748, т.к. 6+8=14, четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой.
Умножение двузначного числа на 101 и на 10101
Самое простое правило: «припишите ваше число к самому себе». При умножении на число 101, 1001, 10101, число надо повторить дважды/трижды:
-
57*101=5757,
-
89*10101=898989.
Умножение на 9, 99 и 999
К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель:
-
286*9=2860–286=2574,
-
23*99=2300–23=2277,
-
18*999=18000–18=17982.
Применение распределительного закона умножения относительно сложения и вычитания ко множителям, один из которых представлен в виде суммы или разности
2.4 Способы быстрого деления чисел
Последовательное деление
Если делитель является составным числом, то разлагаем его на два или большее число множителей, а потом выполняем последовательное деление:
Деление на 0,5, 5, 50 и 500
Чтобы число разделить на 0,5; 5; 50 или 500, надо это число разделить на 1; 10; 100 или 1000 соответственно, и затем результат умножить на 2:
-
21600:50=21600:100*2=432,
-
42400:5=42400:10*2=8480,
-
214000:500=214000:1000*2=428,
-
218:0,5=1218:1*2=436.
Деление на 25, 2,5, 0,25
Чтобы число разделить на 25, надо это число разделить на 100 и умножить на 4:
Чтобы число разделить на 0,25, надо это число умножить на 4:
Чтобы число разделить на 2,5, надо это число разделить на 10 и умножить на 4:
Деление на 125, 12,5, 1,25, 0,125
Чтобы число разделить на 125; 12,5; 1,25; 0,125, надо это число умножить на 8 и разделить на 1000; 100; 10; 1 соответственно:
2. 5 Без карандаша и бумаги
Немецкого ученого Карла Гаусса называли королем математики. Его математическое дарование проявилось уже в детстве. Рассказывают, что в трехлетнем возрасте он удивлял своего отца.
Однажды в школе, Гауссу в то время было 10 лет, учитель предложил классу перечислить все числа от 1 до 100. Пока он диктовал задание, у Гаусса был готов ответ 1+2+3+…..+97+98+99+100=101*50=5050. Как он складывал числа от 1 до 100?
Группируем (1+100)+(2+99)+….=50 пар по 101, а сумма S=101*50.
На олимпиадах такие задачи предлагаются очень часто. Рассмотрим некоторые из них.
Задание 1. Найдите сумму 1+2+3+….+111, решаем аналогично. Ответ: (112*111):2=6216.
Задание 2. Определите пропущенные числа и найдите их сумму. 1+3+5+7+…+77 - это ряд нечетных чисел. Если решать как Гаусс, то решение такое: ((1+77) *39):2=1521.
Данная задача имеет более интересное решение: квадрат числа 1=1;
квадрат числа 2=1+3; квадрат числа 3=1+3+5; квадрат числа 4=1+3+5+7.
Такое открытие было сделано шестилетним Колмогоровым, выдающимся советским математиком - академиком.
Таким образом, 1+3+5+7+….+(2n-1)= n2, в нашей задаче n=39, значит 1+3+5+7+…+77= 392 =1521.
Задание 3. Определите пропущенные числа и найдите их сумму. 1+1+2+3+5+….+144. В этой задаче речь идет о последовательности Фибоначчи1.
В 1202 г. вышло в свет сочинение «Книга об абаке» - знаменитого итальянского математика Леонардо из Пизы, известного больше как Фибоначчи. В ней, решая задачу о размножении кроликов, он получает следующую знаменитую последовательность. Что особенно интересно, что размеры отдельных конечностей тела человека содержат числа из этой последовательности: плечи-2Г, колени-3Г, щиколотка-5Г, руки-8Г, где Г-размер головы. Вся последовательность, до 144 включительно, имеет решение 1+1+2+3+5+8+13+21+34+55+89+144=376.
Задание 4. Как быстро и просто вычислить значение выражения 39-37+35-33+31-29+27-25+…7-5+3-1=(39-37)+(35-33)+…=(2*40):4=2*10=20, (речь идет о парах нечетных чисел).
Задание 5. Сосчитайте: 1+2-3-4+5+6-7-8+9+10-…+2002-2003-2004+2005.
Здесь интересны суммы (2-3-4+5)+(6-7-8+9)+…(2002-2003-2004+2005)-каждая сумма равна 0.
Ответ: 1+501*0=1
Задание 6. У известного русского художника Богданова-Бельского есть картина, изображающая занятия устным счетом. В классе возле доски сидит учитель, а около него стоят ученики, занятые устным решением трудного примера. Ученики сосредоточены и увлечены работой, т.к. пример действительно труден и интересен.
Вот он: 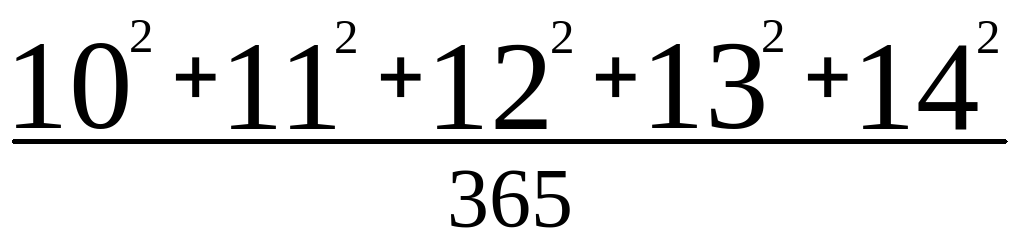 .
.
Решите и вы этот пример устно.
Указание. Искомое число равно 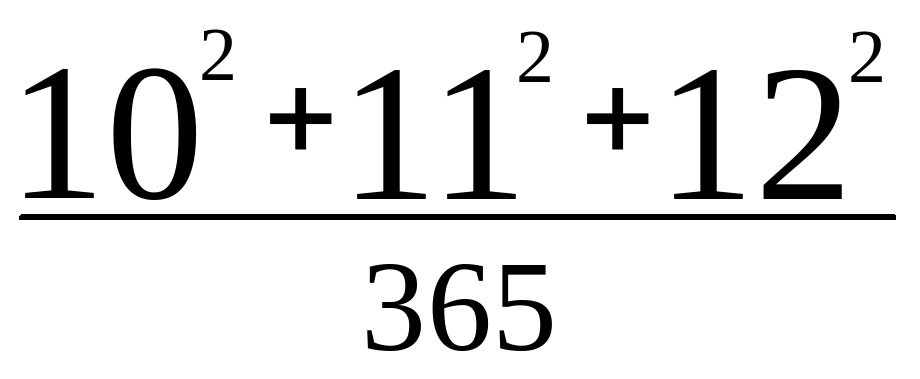 +
+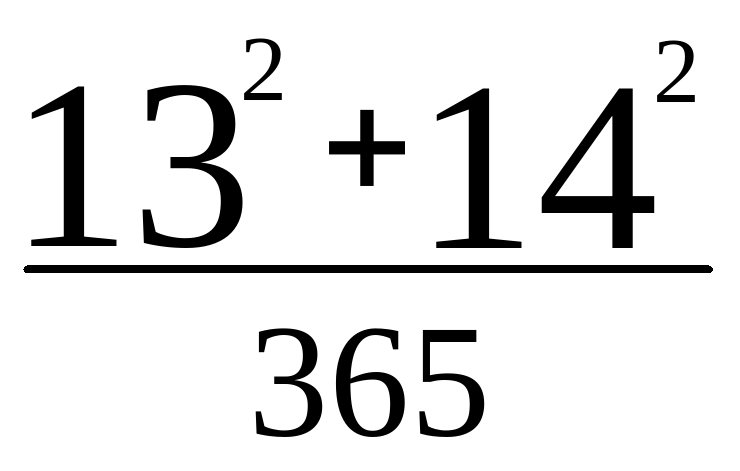 =1+1=2.
=1+1=2.
ГЛАВА III. ДИАГНОСТИКА ВЫЧИСЛИТЕНЫХ НАВЫКОВ У ШКОЛЬНИКОВ
Практическая часть включает в себя изучение динамики развития вычислительных навыков.
В исследовании приняли участия шестиклассники, в количестве 22 человека.
Время проведения: октябрь-февраль.
Этапы исследования:
-
Изучить известные способы быстрого устного счета;
-
Подобрать материал для тренинга;
-
Провести диагностику;
-
Подвести результаты исследования.
Для диагностики был составлен ряд однотипных упражнений, состоящих из 24 примеров на сложение, вычитание, деление и умножение, которые нужно было выполнить за 5 минут (см. Приложение 2 «Материал для тренинга»).
Диагностика проводилась в несколько этапов:
-
Проверка имеющихся навыков устного счета;
-
Изучение способов сложения и вычитания;
-
Ознакомление с новыми приемами умножения;
-
Изучение способов деления.
-
Последний контрольный замер.
Обработка результатов показала:
На первом этапе (октябрь) учащиеся 6 «Б» класса показали: письменно решено – 2%, устно – 31 %, не решено – 67%.
На втором этапе изучения способов сложения и вычитания, во втором контрольном замере (ноябрь), показали: письменно решено – 8,5%, устно – 39,7 %, не решено – 51,8%.
В третьем контрольном замере (декабрь) после изучения способов умножения, процент письменно решенных заданий остался таким же, но вырос процент заданий решенных устно: письменно решено – 8,5%, устно – 48,3 %, не решено – 43,%.
На четвертом этапе (январь) показатели были снижены. Это можно связать с тем, что навык счета, был частично утерян, т.к. учащиеся класса, на зимних каникулах не тренировались в устном счете: – 6,2%, устно – 44,5 %, не решено – 49,3,%..
В феврале, на последнем контрольном замере, учащиеся улучшили свои показатели: теперь самый большой процент решенных заданий приходится на сделанные устно – 58,7%, на втором месте задания, сделанные письменно – 15,3%, сократились так же неправильно решенные задания до 26% (см. рисунок 1).
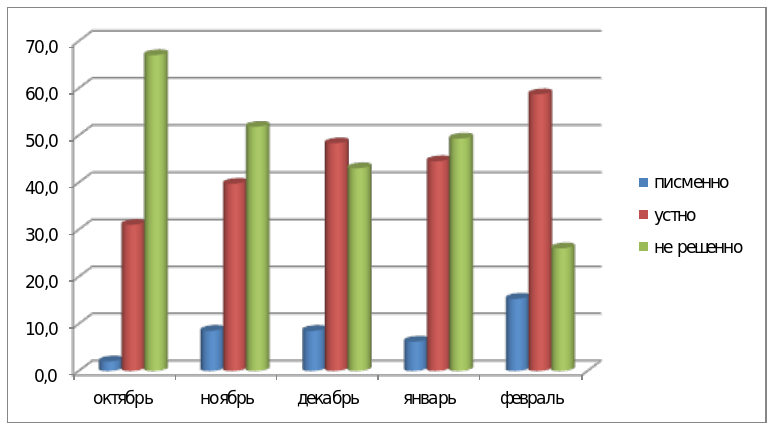
Рисунок 1. Динамика развития вычислительных навыков учащихся
Исходя из результатов исследования, можно сделать следующие выводы:
-
мы подтвердили гипотезу о том, что можно улучшить вычислительные навыки с помощью приемов быстрого счета;
-
вычислительные навыки надо развивать, и, что развить их может каждый школьник, независимо от его феноменальных математических способностей;
-
знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.
ЗАКЛЮЧЕНИЕ
«Математику уже за то любить следует, что она ум в порядок приводит» – говорил Михаил Ломоносов. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных приборов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят вам научиться организовывать себя в различных жизненных ситуациях. Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих.
Необходимым условием успешной работы, так или иначе связанной с вычислениями, является владение культурой счета. Основу культуры счета составляют вычислительные навыки, совершенствование которых возможно только в практической деятельности.
Счет является простым и легким делом только, когда владеешь особыми приемами и навыками. Устный счет развивает механическую память, быстроту реакции, умение сосредоточиться, а поиски и обоснование новых приемов служат формированию логических умений. Каждый ученик может улучшить вычислительные навыки с использованием приемов быстрого счета. Как и насколько он это сделает, зависит, прежде всего, от него самого, от его трудолюбия и стремления. Наработка вычислительных навыков должна быть систематической, ежедневной, надо стремиться к тому, чтобы как можно больше освоить «хитрых» приемов. Без постоянных тренировок, невозможно увеличить свои вычислительные способности, сколько бы ты много приемов не знал.
В заключение подчеркнем, что в школьных учебниках практически нет приемов быстрого счета, а на уроках этому уделяется, не так много времени как хотелось бы, поэтому результат данной работы может служить памяткой для быстрого счета, и будет очень полезной для учащихся 5-6 классов.
Таким образом, цель и задачи, поставленные в начале работы, выполнены, гипотеза подтверждена.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
-
Борода Л.Я., Борисов А.М. Некоторые формы по привитию интереса к математике. //Математика в школе. – 1990, № 11.– С. 39-44.
-
Зайкин М.Н. Математический тренинг. – Москва, 1996. – С. 25-27
-
Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. // Начальная школа. – 1990, №6. – С. 44-46.
-
Иванова Т. Устный счёт. // Начальная школа. – 1999, № 7. – С.11-14.
-
Игнатьев Е.И. В царстве смекалки/ Под редакцией М.К. Потапова, текстол. Обработка Ю.В. Нестеренко. – 4-е изд. – М.: Наука. Главная редакция физико-математической литературы, 1984. – 192 с
-
Липатникова Н.Г. Роль устных упражнений на уроках математики. // Начальная школа. – 1998, № 2. – С. 34-38.
-
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4-8 кл. сред. шк. – 5-е изд. – М.: Просвещение, 1988. – 160 с.: ил.
-
Ткачева М.В. Домашняя математика. – М., Просвещение,1993. – С. 63-65
-
В.Пекелис. Чудо-счётчики – Техника-молодёжи, № 7, 1974 г http://stepanov.lk.net/mnemo/pekelis.html
-
Источник иллюстраций http://www.junior.ru/students/chukhua/shestoe%20chyvstvo.htm
ПРИЛОЖЕНИЕ 1
«ЧУДО СЧЕТЧИКИ»

Теоретический отдел Европейского центра ядерных исследований помимо сложных ЭВМ пользуется также услугами Вильяма Клайна, человека-компьютера.

Арон Чиквашвили

Феноменальный дар к счету проявился у француза Лидоро в три года, когда он не умел еще ни читать, ни писать.

В начале века в России большую популярность приобрел "математик на эстраде" Р. Арраго.

Игорь Шелушков.

Шакунтала Дэви

Прочитав как-то статью о математике-артисте Арраго, Юзеф Приходько вдруг понял, что и он может проделывать подобные номера. Сейчас Приходько - известный в нашей стране математик-моменталист.
ПРИЛОЖЕНИЕ 2 «МАТЕРИАЛ ДЛЯ ТРЕНИНГА»
| I | II |
| 79+26+34+111= | 48*11= |
| 483+126= | 635+249= |
| 5:100= | 196*9= |
| 11*78= | 10*21,3= |
| 5,7*1000= | 0,7:10= |
| 315:25= | 26-19= |
| 168*2,5= | 23*1001= |
| 998*996= | 135+67+65+23= |
| 74*101= | 400:25= |
| 423-95= | 987-125= |
| 654*4 | 543+153= |
| 425:50= | 543:50= |
| 483+126= | 5867+4347= |
| 1908-895= | 396-87= |
| 123+65= | 999*995= |
| 569-565= | 98*8= |
| 356-45-56= | 7687+98= |
| 769+359= | 56-29= |
| 789-648= |
| 124*2,5= |
| 548*99= | 654*50= |
| 16:0,125= | 599+23+67= |
| 459-236= | 569-243= |
| 8656+899= | 129*15= |
| 654*5= | 1994-(1596-456)= |
|
|
|
26





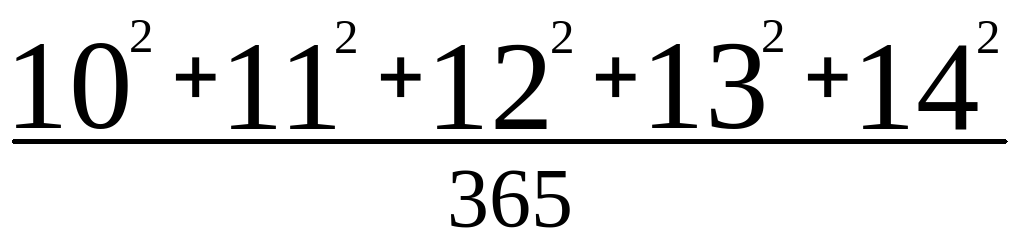 .
.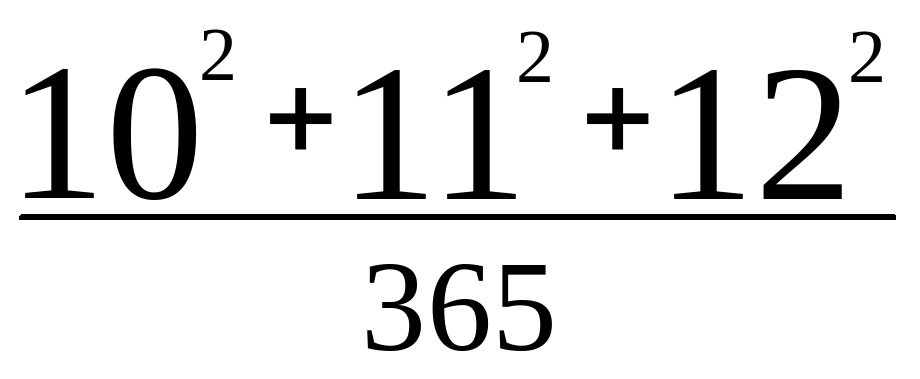 +
+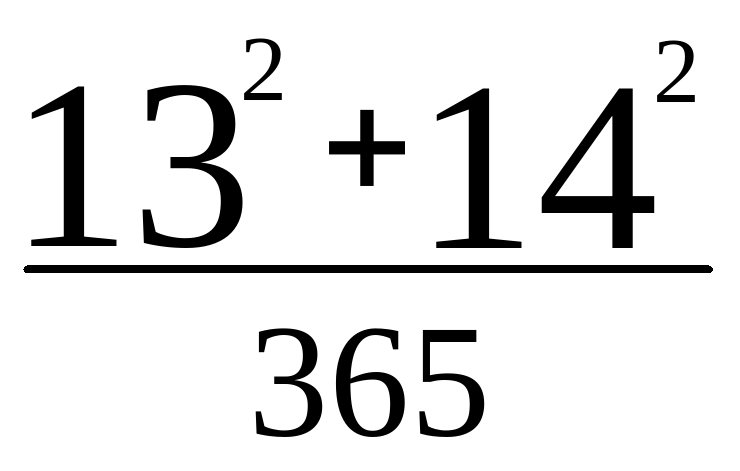 =1+1=2.
=1+1=2.