Разработка банка заданий для подготовки к ЕГЭ по теме:
«Показательные и логарифмические уравнения»
Разработчик: учитель математики Маляр Светлана Витальевна
2023 г
Показательные и логарифмические уравнения и неравенства, несомненно, занимают центральное место в программе математики 10–11-х классов наряду с такими разделами, как тригонометрия, производная и ее приложения. Заданий, связанных, так или иначе, со степенями, корнями, с показательной и логарифмической функциями, в контрольно-измерительных материалах на едином государственном экзамене по математике за последние годы постоянно колеблется.
В связи с разделением итоговой аттестации за курс полной средней школы на два разных по уровню экзамена (базовый и профильный) актуальность рассматриваемой темы не изменилась
Учащиеся 10–11-х классов, изучающие математику на повышенном или углубленном уровне, в большинстве своем планируют поступление в вузы и втузы, где предъявляются повышенные требования к математической подготовке абитуриентов. Поэтому на ЕГЭ по математике им необходимо решить не только задания первой части, но и задания более высокого уровня сложности из второй части, в которых также используются знания по рассматриваемым темам
Проблемы, связанные с изучением темы, заключаются еще и в том, что разнообразие приемов, которые можно использовать при решении заданий, связанных со степенями и логарифмами, значительно шире, чем это представлено в большинстве учебников. К сожалению, того объема знаний и тех типов заданий, которые представлены в большинстве учебников математики, для успешного решения заданий с развернутыми ответами из второй части ЕГЭ оказалось совершенно недостаточно.
Цель: Создать банк заданий логарифмических уравнений повышенного уровня для устранений затруднений при решении данных задач учащимися при подготовке к ГИА-11.
Задачи:
научить учащихся ориентироваться в многообразии свойств функций и алгоритмов решения основных типов заданий по теме
разобраться в сути функционально- графического метода решения уравнений, каковы его разновидности и как научить детей использовать его при решении.
разобрать алгоритмы решения основных типов стандартных и некоторых наиболее часто встречающихся разновидностей нестандартных заданий по рассматриваемой теме
изучить способы решения уравнений.
Объект исследования: процесс обучения учащихся решению логарифмических уравнений и неравенств на уроках математики.
Предмет исследования: методы решения логарифмических уравнений
Гипотеза исследования основана на предположении о том, что знание различных методов решения логарифмических уравнений может повысить эффективность изучения данной темы и качество подготовки обучающихся к сдаче ЕГЭ
Методы исследования: изучение специализированной литературы, анализ, сравнение.
Методы решения логарифмических уравнений.
При решении логарифмических уравнений используют различные методы. Выбор метода зависит от вида уравнения. Перечислим некоторые из них:
Использование определения логарифма
Потенцирование (переход от логарифма данного выражения к самому этому выражению).
Приведение к одному основанию.
Введение новой переменной.
Логарифмирование обеих частей уравнения.
Функционально-графический метод
Уравнения, решаемые подстановкой

| Этапы решения | Содержание | Подводящие задания |
| 1)Введение новой переменной | 
2 - 5 - 5 + 3 = 0 + 3 = 0
| 



|
| 2)Решение квадратного уравнения | 2t2 – 5t + 3 = 0  =1, =1,  
| Квадратное уравнение. Дискриминант: D= D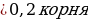 D=0, 1 корень D Корни квадратного уравнения: 
|
| 3) |  = 1 = 1
|  = =
| О пределение логарифма пределение логарифма
|
| Ответ: | X=3 X=3√3 |
|
Задачи для самостоятельного решения
| №п/п | Задание ( решите уравнение) | Ответ |
| 1 | 
| 0,5; 0,25 |
| 2 | 
| -7; 0,5 |

| Этап решения | Содержание | Подводящие задания |
|
1)выписать все условия для решения данного уравнения ИЛИ найти ОДЗ
|

| Вспомнить область определения функции y= Вспомнить область определения функции вида y= |
преобразование выражения
| 
| Вспомнить свойство логарифмов:
|
| 4. преобразование выражения под знаком логарифма | 
| Преобразование выражений |
Введение новой переменной | Пусть  |
|
Составление нового уравнения не содержащего логарифм | m-2=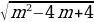 | Свернуть ФСУ: 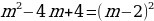 |
Решение уравнения | m-2= ; m-2= ; m-2= | Вспомнить формулу  |
Решение уравнения (7) с учетом выполнения условия, что m-2˃0 |  ; ;
Т.к. функция монотонная, то (х-1)(3х-2-х2)≥0 | ЖЕЛАТЕЛЬНО показать учащимся метод рационализации, т.к. все условия для решения уравнения указаны. |
Решение данного неравенства методом интервалов ИЛИ Решать данное неравенство другими методами | (х-1)(х2-3х+2)≤0 (х-1)(х-1)(х-2)≤0
| Вспомнить теоретический материал по решению неравенств методом интервалов ИЛИ Вспомнить теоретический материал при условии произведения ˃0 |
С учетом условия (ИЛИ ) ОДЗ уравнения | Найти все решения данного неравенства И с учетом ОДЗ выбрать ответ: (2/3;1) (1; (1; |
|
Ответ | (2/3;1) (1; (1; |
|
Задания для самостоятельного решения:
| № п/п | Задание (Решите уравнения): | Ответ |
| 1 | 
| -3; - |
| 2 | 
| 4 |
Решение уравнений смешанного типа,
 =0
=0
| Этап решения | Содержание | Подводящие задания |
|
1. Нахождение области определения логарифма 2 Нахождение области определения дробно- рационального уравнения.
|
Sinx 0
2cosx+ ≠0 ≠0 | Вспомнить область определения функции y= Вспомнить область определения функции вида y= |
| 3 преобразование дробно- рационального уравнения
| 
| Решить уравнение вида 
|
Решение логарифмического уравнения 2 степени | Заменим  
| 4. Решение неполных квадратных уравнений: x (x-3) =0
|
Решение простейших тригонометрических уравнений | 2cosx+√3≠0
| Решение уравнений вида: 
Частные случаи при решении тригонометрических уравнений Sinx=o, sinx=1, sinx=-1 |
| 6 Решение простейших логарифмических уравнений
|  =0 =0
 +2πn, nϵZ +2πn, nϵZ
 =-1 =-1
 +2πn nϵZ +2πn nϵZ
 nϵZ nϵZ

| Решение уравнений вида:  =2 =2
 =0 =0
 =-3 =-3
|
| 7 Вывод о наличии посторонних корней | x≠5π/6+2πn nϵZ
|
|
| 8 Проверка удовлетворению области определения |     1 Y 1 Y
     

 х х
Проверка показывает, что условию sin x 0 и cosx≠ удовлетворяют корни удовлетворяют корни 

| Sinx 0 |
Ответ:
 ;
; 
Задачи для самостоятельного решения:
| Уравнение | Ответ |
|

|
±
|
Уравнения, решаемые с помощью приведения к одному основанию.
Решите уравнение: 
| Этап решения | Содержание | Подводящие задания |
|
1)выписать все условия для решения данного уравнения ИЛИ найти ОДЗ
|
 ОДЗ: (- ОДЗ: (-
|
|
| 2)Провести разложение на линейные множители выражений, стоящих под знаком логарифма | 1. 4 2 2 2. 6 =(3х+7)(2х+3) | Использование формул для решения квадратных уравнений Использование формулы разложения на множители квадратного трехчлена 
|
| 3)Выполнить преобразование левой части уравнения с учетом разложения на множители
| 
|
|
| 4) Преобразование выражения |  , т.к. 2х+3˃0 , т.к. 2х+3˃0

| 

|
| 5)Введение новой переменной | 2 2 Пусть  | |
| 6)Решение нового уравнения не содержащего логарифм | 2y2-3y+1=0
| |
| 7)Обратная замена | 

|
|
| 8)Решение уравнения (7) с учетом ОДЗ | (*): 2х+3=3х+7 х=- 4 (не принадлежит ОДЗ) (**): 2х+3= . . Т.к. 2х+3˃0, (2х+3)2=3х+7 Данное уравнение имеет корни: -2 и - Условию ОДЗ удовлетворяет только число -  | |
Ответ | -  |
|
Задания для самостоятельного решения:
| № п/п | Задание: Решите уравнение | ответ |
| 1 | 3 | 1; 9 |
| 2 | 
| 
|
Уравнения, решаемые с помощью дополнительных сведений из теории логарифмов
Решить уравнение:

| Этап решения | Содержание | Подводящие знания |
| 1.Нахождение области определения логарифма | 


| Вспомнить область определения функции :
 
|
| 2. Решение уравнения с использованием свойств логарифма

 3. Преобразование левой части уравнения с использованием формул сокращённого умножения 3. Преобразование левой части уравнения с использованием формул сокращённого умножения
4. Применение свойства равенства нулю произведения двух множителей. |






| Вспомнить : свойства логарифма: 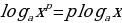
Упростить с помощью Формулы квадрата разности: 
Решить уравнение: 


|
|
5. . Решение простейших логарифмических уравнений вида 
| 
x=a Ответ: x=a, a0,a . .
| Решить уравнение: 
|
| 6.Проверка корней |

Проверка показала, что любое число удовлетворяющее условию

будет являться корнем уравнения. |
Подставим в уравнение  числа, удовлетворяющие области определения логарифма: 
Допустим х=2



|
Ответ: x=a, a0,a≠1.
Апробация




Заключение:
В курсе математики изучаются логарифмические уравнения и способы их решения очень сжато. Потребности учебного процесса требуют от учеников больших знаний и умений.
В материалах на уроке и на олимпиадах часто встречаются задания с логарифмическими уравнениями.
В нашей работе мы рассмотрели различные методы решений логарифмических уравнений и неравенств: использования определения логарифма, потенцирования, перехода к одному основанию, логарифмирования, рационализации, использования свойств логарифмической функции.
Выполняя работу, мы повторили понятие логарифма, его свойства, рассмотрели методы решения логарифмических уравнений и неравенств, применение логарифмической функции.
Результаты данной работы могут быть использованы при подготовке к выпускным и вступительным экзаменам, и на факультативных занятиях для расширения математического кругозора учащихся. В дальнейшем планируя исследовать уравнения в целых числах, способы их решений.
Вся данная деятельность должна привести к более высоким результатам при сдачи егэ.







 - 5
- 5 + 3 = 0
+ 3 = 0

 =1,
=1, 


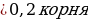











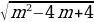
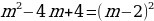
 ; m-2=
; m-2=

 ;
;


 - - +
- - + (1;
(1;



 =0
=0 ≠0
≠0





 =0
=0 +2πn, nϵZ
+2πn, nϵZ +2πn nϵZ
+2πn nϵZ nϵZ
nϵZ



 1 Y
1 Y






 х
х удовлетворяют корни
удовлетворяют корни

 ;
; 




 2
2


 , т.к. 2х+3˃0
, т.к. 2х+3˃0










 .
.









 3. Преобразование левой части уравнения с использованием формул сокращённого умножения
3. Преобразование левой части уравнения с использованием формул сокращённого умножения



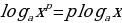



 .
.

















