Совместные и несовместные события. Теоремы о вероятности суммы событий. Условная вероятность.
Теория вероятностей –математическая наука, изучающая закономерности случайных явлений и событий, способных многократно повторяться при воспроизведении определенного комплекса условий.
Испытание – неопределяемое понятие, понимается как наблюдение того или иного явления. Событие – возможный исход того или иного испытания.
Определение1:Результатнаблюдения или эксперимента, который при данном испытании может произойти, а может и не произойти, называется случайным событием.
Определение2:Событие, которое обязательно наступает при каждом испытании, называется достоверным.
Определение3:Событие, которое заведомо не может произойти, называется невозможным.
Определение4:Два события называются равносильными, если при каждом испытании они либо оба наступают, либо оба не наступают.
Определение5:События, которые не могут произойти одновременно в результате испытания, называются несовместными.
Определение6: Под множеством элементарных событийзадачи понимают полное множество взаимоисключающих исходов эксперимента.
Пример: 1) Пусть эксперимент состоит в подбрасывании монеты. Два элементарных события: «выпадание орла» и «выпадание решки».
2) Пусть эксперимент состоит в подбрасывании кости. Шесть элементарных событий: выпадание единицы на верхней грани кости, выпадание двойки, тройки и т.д…
Определение7 (классическое определение вероятности): Вероятностью события называется число, равное отношению числа исходов испытания, благоприятствующих событию (m) к числу всевозможных исходов испытания (n).
Обозначается: P(A)= 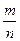 , P – вероятность случайного события, A – само событие.
, P – вероятность случайного события, A – само событие.
Примеры:
1) Пусть эксперимент состоит в подбрасывании монеты. Два элементарных события: «выпадание орла» и «выпадание решки», значит n=2. Тогда вероятность события-«выпадание орла» равна P(A)= 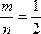 , где m=1.
, где m=1.
2) Пусть эксперимент состоит в подбрасывании кости. Шесть элементарных событий: выпадание единицы на верхней грани кости, и т.д… Вероятность события «выпадание шести очков на грани кости» равна P(A)= 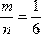 , где m=1.
, где m=1.
Определение 8. Событие (А и B), т. е. событие, состоящее в наступлении обоих событий А и B, называется произведением событий А и B и обозначается через АB
Определение 9. Событие (А или B), т. е. событие, состоящее в наступлении хотя бы одного из событий А и B, называется суммой событий А и B и обозначается через А+B
Теорема сложения вероятностей (для попарно несовместимых событий): вероятность того, что произойдет хотя бы одно из попарно несовместимых событий, равна сумме вероятностей этих событий P(A+B+ C) = P(A) + P(B) + P(C).
Теорема произведения вероятностей (для попарно независимых событий): вероятность того, что произойдут одновременно независимые события, равна произведению вероятностей P(A•B) = P(A) • P(B).
Задача 1.В двух коробках лежат карандаши.В первой коробке – 4 синих и 3 красных карандаша. Во второй коробке – 2 синих, 2 красных. Одновременно из двух коробок извлекают по одному карандашу. Найти вероятность того, что оба карандаша окажутся красными.
Решение: Пусть А- событие, что вынут красный карандаш из первой коробки. По классическому определению вероятности P(A)= 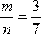 , где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)=
, где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)= 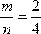 . Тогда по теореме произведения вероятностей, так как события происходят одновременно P(A•B) = P(A) • P(B) =
. Тогда по теореме произведения вероятностей, так как события происходят одновременно P(A•B) = P(A) • P(B) = 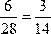 .
.
Случайная величина - величина, которая при каждом испытании принимает то или иное числовое значение (наперед неизвестно, какое именно), зависящее от случайных причин, которые заранее не могут быть учтены. Случайные величины обозначают заглавными буквами латинского алфавита, а возможные значения случайной величины – малыми. Так, при бросании игрального кубика происходит событие, связанное с числом x , где x – выпавшее число очков. Число очков – случайная величина, а числа 1, 2, 3, 4, 5, 6 – возможные значения этой величины. Расстояние, которое пролетит снаряд при выстреле из орудия – тоже случайная величина (зависит от установки прицела, силы и направления ветра, температуры и других факторов), а возможные значения этой величины принадлежат некоторому промежутку (a; b).
Дискретная случайная величина – случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.
Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины – бесконечно.
Например, число выпавших очков при бросании кубика, балльная оценка за контрольную работу – дискретные случайные величины; расстояние, которое пролетает снаряд при стрельбе из орудия, погрешность измерений показателя времени усвоения учебного материала, рост и вес человека – непрерывные случайные величины.





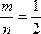 , где m=1.
, где m=1.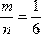 , где m=1.
, где m=1.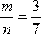 , где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)=
, где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)= 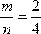 . Тогда по теореме произведения вероятностей, так как события происходят одновременно P(A•B) = P(A) • P(B) =
. Тогда по теореме произведения вероятностей, так как события происходят одновременно P(A•B) = P(A) • P(B) = 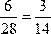 .
.









