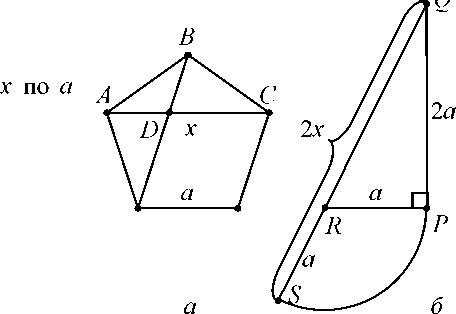ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ С ПРЕПЯТСТВИЯМИ И ОГРАНИЧЕНИЯМИ
Решение задач на построение с препятствиями и ограничениями
Новокузнецк 2024
ОБЩИЕ АКСИОМЫ КОНСТРУКТИВНОЙ ГЕОМЕТРИИ И ИНСТРУМЕНТЫ ПОСТРОЕНИЯ
Раздел геометрии, в котором изучаются геометрические построения, называется конструктивной геометрией.
Основным понятием конструктивной геометрии является понятие построить геометрическую фигуру.
Это понятие принимается без определения, конкретный его смысл известен из практики, где оно означает: начертить, провести (линию), отметить (точку). В интересах логической строгости изложения основное понятие конструктивной геометрии - построить фигуру - характеризуется через основные требования (общие аксиомы конструктивной геометрии).
Рассмотрим эти аксиомы.
I. Каждая данная фигура построена, т.у. если о какой-либо фигуре сказано, что она дана, то под этим подразумевается, что она уже изображена, начерчена, по-другому говоря, построена.
2. Если даны две фигуры, то построено:
а) их объединение
б) пересечение
в) разность (если она не равна пустому множеству)
3. Если дана некоторая фигуpa, то можно построить точку:
а) принадлежащую данной фигуре
б) не принадлежащую ей.
Решая задачи на построение, будем строить новые точки и линии, обладающие некоторыми определенными, указанными свойствами, пользуясь инструментами геометрических построений. Необходимо располагать точными и, для математических целей, полным описанием того или иного инструмента. Такое описание дается в виде аксиом.
Аксиома линейки. Линейка позволяет выполнить следующие геометрические построения:
а) построить отрезок, соединяющий две построенные точки;
б) построить прямую, проходящую через две построенные точки;
в) построить луч, исходящий из построенной точки и проходящий через другую построенную точку.
Аксиома циркуля. Циркуль позволяет выполнить следующие геометрические построения:
а) построить окружность, если построены центр окружности и концы отрезка, равного радиусу окружности;
б) построить любую из двух дополнительных дуг окружности, если построен центр окружности и концы дуги.
Аксиома двусторонней линейки. Двусторонняя линейка позволяет: а) выполнить любое построение, выполнимое линейкой; б) в каждой из полуплоскостей, определяемых построенной прямой, построить прямую, параллельную этой прямой и проходящую от нее на расстоянии h, где h - фиксированный элемент для данной двусторонней линейки (ширина); в) если построены две точки А и В, то установить, будет ли АВ h, и если AB h , то построить 2 пары параллельных прямых, проходящих соответственно через А и В и отстоящих одна от другой на расстоянии h.
Аксиомы угла. Угол позволяет: а) сделать все построения, выполнимые линейкой; б) через данную точку плоскости провести под углом α к некоторой данной прямой; в) если построены отрезок АВ и фигура Ф , то установить, содержит ли фигура Ф точку, из которой отрезок АВ виден под углом α , и если такая существует, то построить ее.
В частности циркуль и линейка позволяют выполнить следующие основные построения:
Построить отрезок, соединяющий две построенные точки.
Построить прямую, проходящую через две построенные точки.
Построить луч, исходящий из построенной точки и проходящий через другую построенную точку.
Построить окружность, если построены центр и концы отрезка, равного радиусу окружности.
Построить любую из двух дополнительных дуг окружности, если построены центр окружности и концы дуги.
Построить любое конечное число точек пересечения двух построенных фигур, если такие точки существуют.
Построить точку, принадлежащую какой-либо построенной фигуре.
Построить точку, заведомо не принадлежащую какой-либо построенной фигуре.
Задача на построение состоит, в том, что требуется построить указанными инструментами фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и данной. Каждая фигура, удовлетворяющая условию задачи, называется решением задач [10, c. 35].
Найти решение задачи на построение - значит указать конечную последовательность основных построений, после выполнения которых искомая фигура будет считаться построенной в силу принятых аксиом конструктивной геометрии. Перечень основных построений, а следовательно, и ход решения задачи, зависит от употребляемого набора инструментов. Следует заметить, что такой подход в определении нахождения решения не рациональный. Иногда целесообразнее укрупнить шаги построения.
Рассматривают как шаг построения целые блоки основных построений. Эти блоки представляют собой решения элементарных задач на построение. Их назовем элементарными построениями. Тогда можно дать следующее определение.
Решить задачу на построение - это значит указать такую конечную последовательность основных (ОП) и элементарных построений (ЭП), после выполнения которых искомая фигура может считаться построенной в силу общих аксиом конструктивной геометрий.
В качестве элементарных построений (ЭП) возьмем следующие задачи.
ЭП I. Отложить на данном луче от его начала отрезок, равный данному отрезку.
ЭП 2. Отложить от данного луча в данную полуплоскость угол, равный данному углу.
ЭП 3. Построить треугольник по трем сторонам.
ЭП 4. Построить треугольник по двум сторонам и углу между ними.
ЭП 5. Построить треугольник по стороне и двум прилежащим углам.
ЭП 6. Построить биссектрису данного неразвернутого угла.
ЭП 7. Построить серединный перпендикуляр данного отрезка.
ЭП 8. Построить середину данного отрезка.
ЭП 9. Построить прямую, проходящую через данную точку и перпендикулярную данной прямой. (При этом данная точка может лежать на данной прямой, может и не лежать на ней).
ЭП 10. Построить прямую, проходящую через данную точку и параллельную данной прямой.
ЭП 11. Построить прямоугольный треугольник по гипотенузе.
ЭП 12. Построить прямоугольный треугольник по гипотенузе и катету.
ЭП 13. Построить касательную к окружности, проходящую через данную на ней точку.
Иногда условиям задачи на построение удовлетворяют несколько фигур. Решить задачу на построение - значит найти все ее решения.
Поясним это определение. Фигуры, удовлетворяющие условию задачи, могут отличаться размерами, формой и положением на плоскости. Фигуры, удовлетворяющие условию задачи, отличающиеся размерами или формой, будем считать различными. С расположением дело обстоит так.
Если условие задачи не предусматривает определенного расположения искомой фигуры относительно данных фигур, то задача считается решенной, если:
а) построено некоторое число неравных фигур Ф1,…, Ф2 удовлетворяющих условию задачи,
б) доказано, что всякая фигура, удовлетворяющая условию задачи, равна одной из них; считается, что задача имеет n решений (о точностью до равенства).
Если условие задачи предусматривает определенное расположение искомой фигуры относительно какой-либо данной фигуры, то задача считается решенной, если:
а) построено некоторое число фигур, удовлетворяющих условию задачи [3, c. 19].
б) доказано, что любая фигура, удовлетворяющая условию задачи, совпадает с одной из них. При этом равные фигуры, но различно расположенные, считаются различными решениями. Замечание.
Встречаются задачи, имеющие бесконечное множество решений. Такие задачи называются неопределенными. Очевидно, все решения нельзя построить. В связи с этим вопросом: когда же считать неопределенную задачу решенной?
Решение неопределенной задачи ищется в параметрической форме: указывается прием построения фигур, удовлетворяющих условию задачи, причем эти фигуры определяются выбором определенного положения одной точки на некоторой данной фигуре. Эти точки играют роль геометрического параметра. Задача считается решенной, если при всевозможных допустимых положениях произвольной точки возникают все фигуры, удовлетворяющие условию задачи.
Встречаются задачи такие, что не существуют фигур, удовлетворяющих условию задачи. Например, в параллелограмм (не ромб) нельзя вписать окружность. Нельзя провести прямую через 2 данные точки одним лишь циркулем.
Во всех этих случаях решить задачу на построение - значит доказать, что искомая фигура не существует, или доказать, что она не может быть построена данными средствами.
Условие задачи часто дает известный простор в выборе данных. Например, если требуется построить треугольник по трем сторонам, то данными являются три отрезка, которые могут быть произвольными по величине и положению. Задача в такой формулировке считается решенной, если она решена для всех принципиально различных предположений относительно выбора данных.
Может оказаться, что при таком выборе данных задача решается иначе, чем при другом их выборе, поэтому приходится рассматривать ряд отдельных случаев и давать решение задачи для каждого из них.
ПЛАНИМЕТРИЧЕСКАЯ ЗАДАЧА НА ПОСТРОЕНИЕ И СХЕМА ЕЕ РЕШЕНИЯ
При решении сложных задач основную трудность представляет вопрос о том, как найти способ решения. Решение этого вопроса облегчается, если придерживаться определенной схемы рассуждений. Эта схема состоит из четырех этапов: анализ, построение, доказательство, исследование.
Анализ: сначала подразумеваем, что задача решена и искомая фигура построена. Делаем схематически чертеж и, используя все известные теоремы планиметрии, находим связь между данными элементами и искомой фигурой. Этих зависимостей должно быть достаточно, что бы фигура могла быть построена с помощью только циркуля и линейки (или только одного из инструментов).
Построение: используем только данные элементы задачи. Исходя из анализа, строим данную фигуру.
Доказательство: используя данные анализа и все шаги построения докажем, что построенная фигура удовлетворяет всем условиям задачи.
Исследование: прежде всего, определить имеет ли задача решение, поясняем почему. Затем определяем количество решений задач. Количество решений зависит от условия задачи и положения искомой фигуры на плоскости.
К первому типу относят задачи, где положение фигуры относительно данных элементов не играет никакой роли. Здесь достаточно только отметить имеет или нет задача решение.
Ко второму типу относят задачи, в которых положение искомой фигуры зависит от данных элементов, то есть данных фигур. [3]
Для иллюстрации сказанного рассмотрим следующий пример.
Задача. Построить треугольник, если известны: длина основания а, угол при основании α и разность двух других сторон d.
Решение. Заметим, что в условии задачи не указаны инструменты. B таких случаях будем полагать (как и в школе), что задачу надо решить с помощью линейки и циркуля.

 Анализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC - искомый треугольник: AB = a, AC–BC = AD=d,
Анализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC - искомый треугольник: AB = a, AC–BC = AD=d, 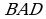 =. Замечаем, что ∆АВD = определен по двум сторонам и углу между ними.
=. Замечаем, что ∆АВD = определен по двум сторонам и углу между ними.
Третья вершина С искомого треугольника может быть найдена как точка пересечения луча АD и прямой l - серединного перпендикуляра отрезка ВD). Иначе говоря план решения найден, строим треугольник ∆АВD, а затем и третью вершину С.
Построение. В этом пункте реализуем план решения.
Строим последовательно:
1) 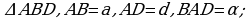
2) l, l – серединный перпендикуляр отрезка BD;
3) C, C = [AD) ∩ l.
Треугольник АВС – искомый.
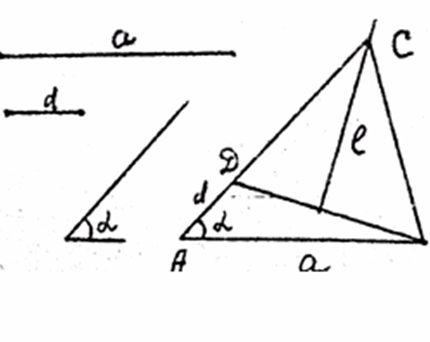
Рисунок 1 – Чертеж к задаче на построение треугольника
Доказательство. Действительно, ∆АВС удовлетворяет всем условиям задачи, т.к. по построению АВ = а, АС – ВС = АD = d, BAD = α.
Исследование. Проверил каждый шаг построения на осуществимость и единственность. Первый шаг возможен и единственен тогда и только тогда, когда 0dcosα. Действительно, если d a cos α, то прямая l пересекает луч AD.
Но вернемся к анализу. У нас задача решена, предполагая, что α лежит против меньшей из двух боковых сторон. Если α лежит против большей стороны, то предыдущий метод построения не проходит. Как быть? По теории мы должны и для этого случая дать решение. Нетрудно убедиться, что ΔABF определен (a,d и угол π - α). Построение, доказательство и исследование провoдятcя так же, как и выше.
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НА ПОСТРОЕНИЕ
Суть любого из методов геометрических построений – построение в конечном счете отдельных точек, которыми определяется данная фигура.
Метод пересечений (метод ГМТ)
ГМТ – множество точек плоскости (фигуры), выделяемых из всех точек плоскости по каким – либо признакам (свойствам).
Суть метода пересечений: Пусть нужно построить точку Х, удовлетворяющую двум данным условиям, и F1 и F2 – множество точек, удовлетворяющих каждому из условий в отдельности, тогда искомая точка Х – точка пересечения множеств F1 и F2.
Заметим, что успех от применения этого метода полностью зависит от знания конкретных ГМТ. Наиболее часто применяются следующие геометрические места точек:
ГМТ 1. Множество точек плоскости, каждая из которых равноудалена от двух данных точек А и В, есть серединный перпендикуляр отрезка АВ.
ГMT 2. Множество точек, находящихся на данном расстоянии от данной прямой, есть две прямые, параллельные данной и стоящие от нее на данном расстоянии.
ГМТ 3. Множество точек, каждая из которых равноудалена от двух данных параллельных прямых, есть прямая, являющаяся их осью симметрии.
ГМТ 4. Множество точек, каждая из которых равноудалена от двух пересекающихся прямых, есть две взаимно перпендикулярные прямые, содержащие биссектрисы углов, образованных данными прямыми,
ГМТ 5. Множества точек плоскости, из которых отрезок АВ виден под прямым углом, есть окружность (без точек А и В ), построенная на отрезке АВ как на диаметре.
ГМТ 6. Множество точек плоскости, из которых отрезок АВ виден под углом α, где α ≠ 90є, α ≠ 180є , есть две дуги с общими концами А и В (без точек А и В), симметричные относительно прямой АВ.
ГМТ 7. Множество точек плоскости, из которых данная окружность видна под углом α, где α ≠ π, есть окружность,- концентрическая с данной, радиус которой больше радиуса данной окружности.
ГМТ 8. Множество точек, делящих всевозможные хорда окружности (O, ОА), проведенные через точку А окружности, в одном и том же отношении λ, где λ 0, есть окружность (без точки А) с центром на прямой ОА, проходящая через точку А. Если λ = 1, то эта окружность построена на отрезке ОА как на диаметре.
ГМТ 9. Множество точек плоскости, для каждой из которых разность квадратов расстояний от двух данных точек А и В постоянна, есть прямая, перпендикулярная прямой АB.
ГМТ 10. Множество точек плоскости, для каждой из которых сумма квадратов расстояний до двух данных точек А и В равна а2, есть окружность с центром в середине отрезка АВ, если 2а2AB2; середина отрезка AB, если 2a2 = AB2; и пустое множество, если 2a2c. 32].
ГМТ 11. Множество точек плоскости, для каждой из которых отношение расстояний до двух данных точек А и В постоянно и отлично от единицы, есть окружность с центром на прямой АВ (окружность Аполлония).
Метод геометрических преобразований
Метод геометрических преобразований конкретизируется через метод параллельного переноса, метод поворота, метод осевой симметрии, метод центральной симметрии, метод подобия.
Суть метода: Первоначально вместо искомой фигуры строится вспомогательная фигура, которую легче построить, заменяя или отбрасывая при этом одно из условий; затем с помощью каких-либо геометрических преобразований вспомогательная фигура или ее часть преобразуются в искомую фигуру.
Например:
-построение треугольника по двум углам и биссектрисе третьего угла;
-построение прямоугольного треугольника по гипотенузе и отношению катетов [1, c. 34].
Алгебраический метод
Суть метода: решение задачи на построение сводят к построению некоторого отрезка (или нескольких отрезков). Длину искомого отрезка выражают через длины известных отрезков с помощью формулы. Затем строят искомый отрезок по полученной формуле. Причем, так как длина отрезка выражается линейными единицами, следовательно, на функцию, определяющую искомый отрезок, должно налагаться определенное условие, а именно, это должна быть однородная функция первого порядка. Кроме того, функция должна быть операцией извлечения корня (если она есть), то только степени 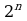 (Например: построение отрезка, являющегося средними геометрическими двух других отрезков.).
(Например: построение отрезка, являющегося средними геометрическими двух других отрезков.).
Метод оригами - практический метод, основанный на перегибании (реальном или мысленном).
Возможности перегибания листа бумаги включают в себя не только «геометрию линейки», но и «геометрию циркуля», что обеспечивает возможность решения большого числа разнообразных задач как серьезных, так и забавных.
Решение задачи методом оригами бывают часто более наглядными и понятными.
Некоторые задачи, решаемые методом оригами, имеют решение с помощью циркуля и линейки (например, деление угла на три равных части).
Рассмотрим пример решения задачи методом ГМТ
Задача 1. Построить треугольник ABC по стороне a=BC, опущенной на неё высоте ha и противолежащему углу . [13, c. 35].
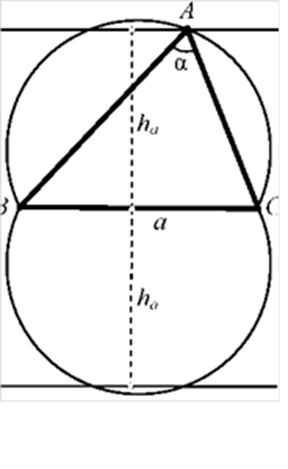
Рисунок 2 – Чертеж к задаче 1
Анализ:
Первое условие говорит, что A находится на расстоянии ha от прямой BC. Множество точек, удовлетворяющих этому условию, - это пара параллельных прямых, отстоящих от BC на это расстояние. Согласно второму условию, отрезок BC виден под углом ABC=. Такое ГМТ- есть пара дуг, симметричных относительно BC.
Значит, A - любая из точек пересечения пары прямых с парой дуг. В силу симметрии картинки все получающиеся треугольники равны, поэтому на самом деле решение нашей задачи единственно (или вообще не существует).
Рассмотрим пример решения задачи методом геометрических преобразований.
Задача 2. Через точки А и B, данные по одну сторону от прямой l, провести окружность, касающуюся l.
Анализ: Рассмотрим случай, когда прямая AB не параллельна и не перпендикулярна l (рис. 2).

Рисунок 3- Чертеж к задаче 2
Проведем серединный перпендикуляр p к отрезку AB и отразим относительно него прямую l. Искомая окружность должна касаться и отраженной прямой т. Таким образом, с помощью осевой симметрии мы свели задачу к другой, более известной (во всяком случае, эта вторая задача встречается в стандартных школьных учебниках): вписать в угол (со сторонами l и т) окружность, проходящую через данную точку A (через B такая окружность пройдет автоматически). Эту вспомогательную задачу также можно решить с помощью преобразования, на сей раз - гомотетии. Любая вписанная в угол окружность гомотетична искомой относительно вершины O угла с коэффициентом k=OA/OA где A - одна из точек ее пересечения с прямой OA. Поэтому достаточно вписать в угол любую окружность ω, а потом растянуть (или сжать) ее в k раз. В рассматриваемом случае задача имеет два решения, т.к. прямая OA пересекает окружность в двух точках [4, c. 46].
Пример применения алгебраического метода, при котором нужные для построения отрезки или углы выражаются формулами через данные, а вычисления по этим формулам производятся прямым построением, дает построение правильного пятиугольника (рис. 3а). Обозначая его сторону через а, а диагональ через х и пользуясь подобием треугольников ABC и BDA, получаем:
AB : AC = AD : AB = (AC - CD) : AB или а : х = (х- а) : а (т. к. CD = BC = AB = а), показано на рис. 3.
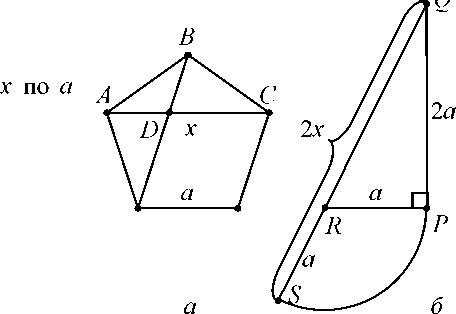
Рисунок 4 – Чертеж к примеру применения алгебраического метода
РЕШЕНИЕ ЗАДАЧ НА ПОСТРОЕНИЕ С ПРЕПЯТСТВИЯМИ И ОГРАНИЧЕНИЯМИ
Рассмотрим решение задач на построение с препятствиями и ограничениями.
Задача №1. Пользуясь только циркулем: 1) постройте точку, симметричную данной точке А, относительно прямой, заданной точками Б и С; 2) из данной точки А опустите перпендикуляр на данную прямую ВС, т. е. постройте еще одну точку перпендикуляра к ВС, проходящего через А.
Решение:
1) Построим окружность с центром в точке А, так, чтобы она пересекала ВС в двух точках F и Е. Отрезок АЕ будет равен АF. Построим две окружности с центрами в точках F и Е, с радиусами АF=АЕ. Они пересекутся в точке А и точке А1, которая будет симметрична точке А, относительно ВС.
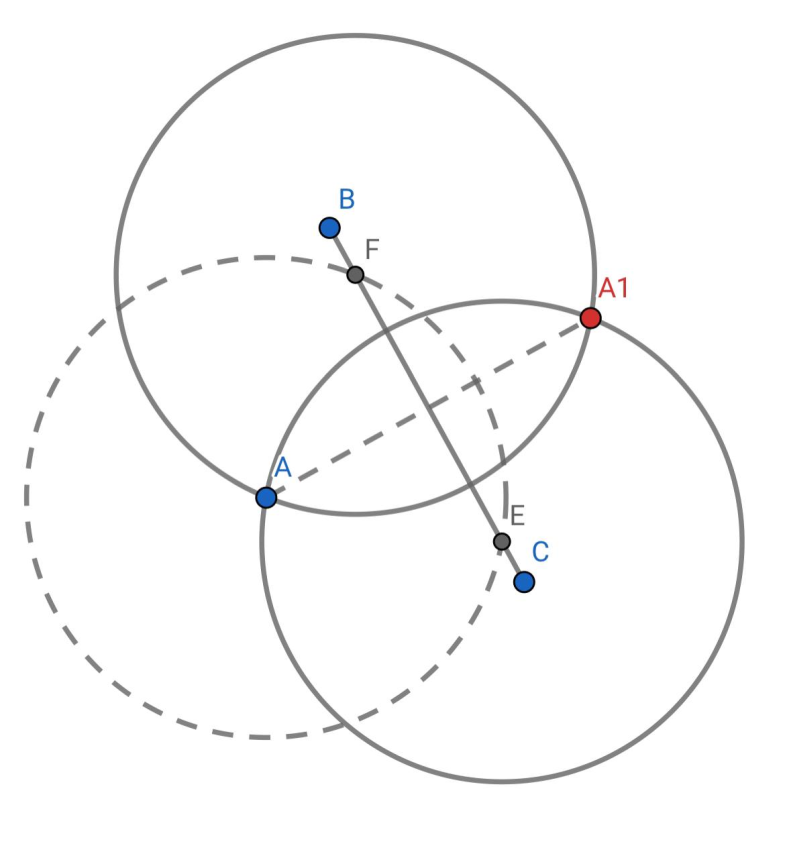
Рисунок 5 - Чертеж к задаче №1, 1)
2)Построим окружность с центром в точке А, так, чтобы она пересекала ВС в двух точках F и Е. Отрезок АЕ будет равен АF. Построим две окружности с центрами в точках F и Е, с радиусами АF=АЕ. Они пересекутся в точке А и точке G, которая будет симметрична точке А, относительно ВС. Тогда AG будет перпендикулярно ВС.
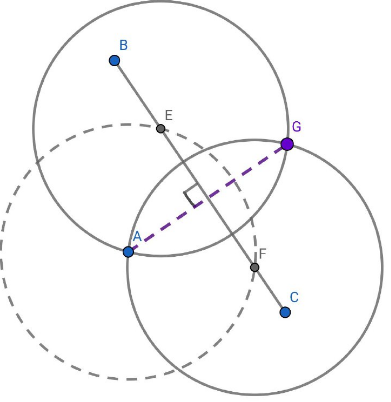
Рисунок 6 - Чертеж к задаче №1, 2)
Задача №2. Вершина А треугольника ABC не уместилась на чертеже. Как построить высоту этого треугольника к стороне ВС?
Решение:
Отобразим стороны АВ и АС симметрично относительно ВС до их пересечения в точке F. Получим симметричные треугольники ABC и FBC. В полученном треугольнике FBC проведем высоту к стороне ВС, получим точку G, из которой симметрично отобразим высоту GF (относительно ВС) до точки А, получим высоту треугольника АВС - AG.
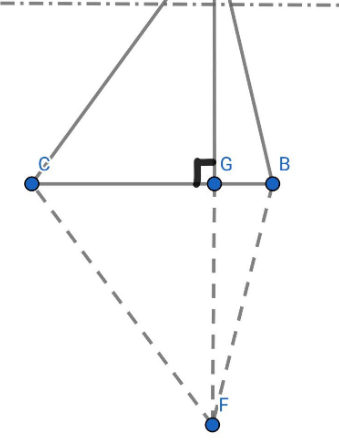
Рисунок 7 - Чертеж к задаче №2
Задача №3. Как в треугольнике, одна из вершин которого не уместилась на чертеже, провести медианы?
Решение:
Пусть точка А треугольника АВС не поместилась на чертеже. Отобразим стороны АВ и АС симметрично относительно ВС до их пересечения в точке F. Получим симметричные треугольники ABC и FBC. В полученном треугольнике FBC проведем медианы ко всем сторонам, которые пересекаются в точке J. Отобразим симметрично относительно ВС точку пересечения медиан, назовем ее К. Точка G - середина стороны ВС. Проведем медианы в треугольнике АВС: ВК до пересечения стороны СА в точке L, CK до пересечения стороны АВ в точке М и GK до точки А.
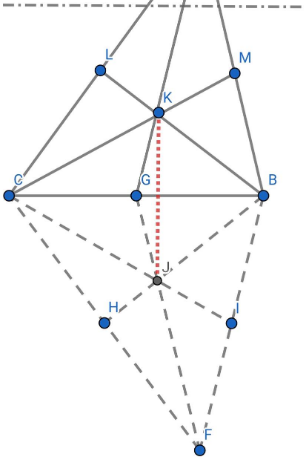
Рисунок 8 - Чертеж к задаче №3
Задача №4. Даны две точки А и В. Как с помощью циркуля и линейки провести через эти точки прямую линию, если линейки короче расстояния между ними?
Решение:
Построим две окружности с одинаковыми радиусами и с центрами в точках А и В. Обозначим точки пересечения этих окружностей как E и F. Отрезок EF будет серединным перпендикуляром между точками А и В. Аналогично построим две равные окружности с центрами в точках Е и F. Они пересекутся в точках К и L, KL - серединный перпендикуляр между Е и F. КL пересекает EF в точке J, эта точка будет являться серединой отрезка АВ. Теперь, чтобы провести отрезок АВ, необходимо провести отрезки AJ и JB.17:49
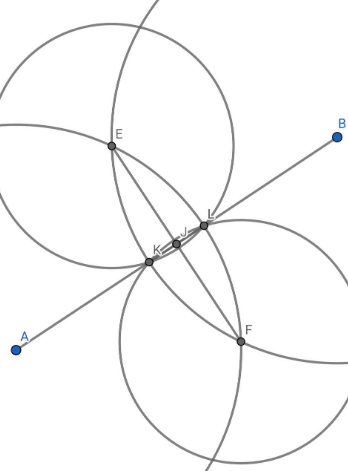
Рисунок 9 - Чертеж к задаче №4
Задача №5. Даны точка А и прямая, заданная двумя ее точками В и С. Пользуясь только циркулем, постройте такую точку D, чтобы отрезки AD и ВС лежали на параллельных прямых.
Решение:
Построим две окружности с одинаковыми радиусами с центрами в точках В и С. Они пересекаются в точках F и G. Проведем прямую FG. Построим окружность с центром в точке А, так, чтобы она пересекала FG в двух точках K и I. Построим две окружности с одинаковыми радиусами с центрами в точках K и I. Они пересекаются в точках M и N. Прямая АМ будет параллельна ВС, следовательно на этой прямой можно выбрать точку D и тогда отрезок AD будет параллелен отрезку ВС.
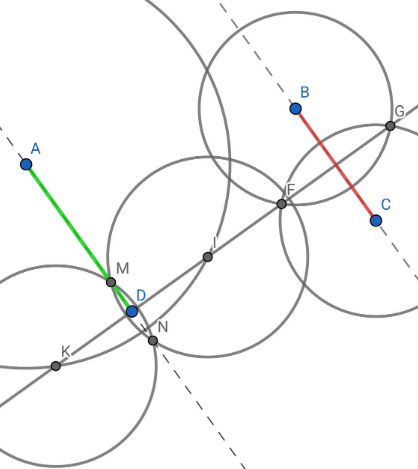
Рисунок 10 - Чертеж к задаче №5
Задача №6. Даны две точки А и В. Требуется, пользуясь только циркулем, построить точку, которая лежала бы на прямой, определяемой точками А и В. Как это сделать?
Решение:
Построим две окружности с одинаковыми радиусами и с центрами в точках А и В, они пересекутся а точках Е и F. ЕF - серединный перпендикуляр между А и В. Аналогично построим две окружности с центрами в точках Е и F. Они пересекутся в двух точках, которые и будут лежать на прямой АВ. Так, например, точка I принадлежит АВ.
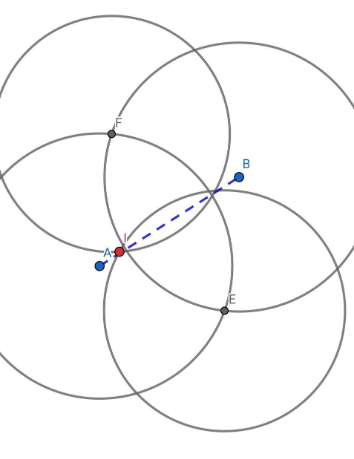
Рисунок 11 - Чертеж к задаче №6
Задача №7. Пользуясь только циркулем, постройте углы в 30°, 60° и 90°.
Решение:
Возьмем произвольную точку С и прямую АВ, не проходящую через точку С. Построим окружность с центром в точке С, так, чтобы она пересекала АВ в двух точках Е и F. Построим две окружности с одинаковыми радиусами и с центрами в точках Е и F. Они пересекаются в точках I и J. Точки С, I и J будут лежать на одной прямой, перпендикулярной АВ, получим угол равный 90 градусам. Построим окружность с центром в точке С и радиусом равным 2СК. Пусть она пересекает прямую АВ в точке А, тогда АС- радиус окружности, АС=2СК. Рассмотрим треугольник АСК, угол К=90 градусов, АС=2СК, следовательно угол А равен 30 градусам (катет лежащий против угла в 30 градусов равен половине гипотенузы). Тогда угол С в треугольнике АСК = 180-90-30=60 градусов.
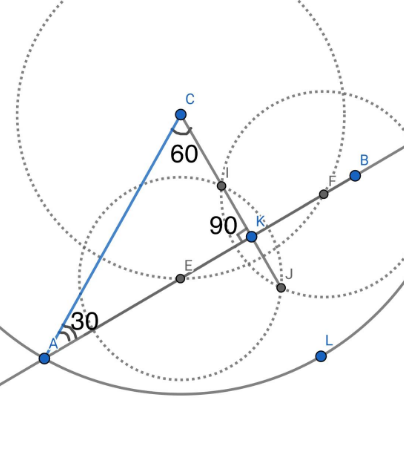
Рисунок 12 - Чертеж к задаче №7
Задача №8. Вершина С треугольника ABC не уместилась на чертеже. Постройте основания высоты и биссектрисы, проведенных из вершины С.
Решение:
Отобразим симметрично стороны треугольника до их пересечения, получим точку С1. Из С1 проводим высоту C1H и биссектрису C1L. Из полученных точек, симметрично отобразим высоту и биссектрису треугольника ABC.
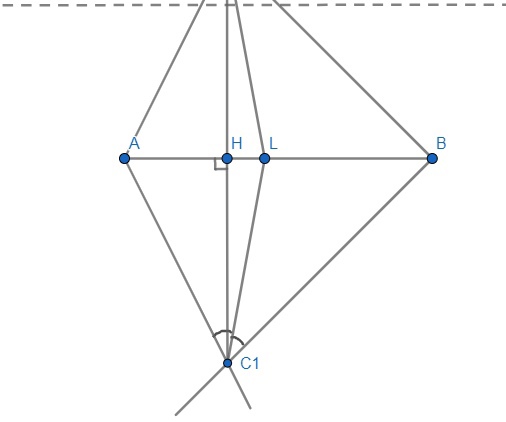
Рисунок 13 - Чертеж к задаче №8
Задача №9. Вершина угла ABC недоступна, D — внутренняя точка этого угла. Придумайте несколько способов построения прямой BD.
Решение:
Отобразим симметрично стороны треугольника до их пересечения, получим точку B1. Относительно стороне АВ симметрично отобразим точку D1, соединив с вершиной В1. Симметрично строим прямую ВD.
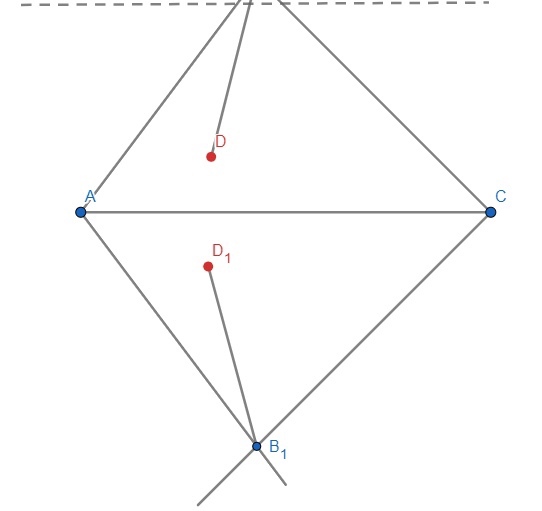
Рисунок 14 - Чертеж к задаче №9
Задача №10. Дан отрезок AB, расположенный на самом краю листа бумаги. Требуется к этому отрезку через его середину провести перпендикуляр. Как это сделать?
Решение:
Построим две окружности с одинаковыми радиусами с центрами в точках А и В, так чтобы они имели две точки пересечения, отметим точку , которая поместилась на чертеже. Аналогично построим окружности чуть меньшего радиуса, но чтобы они пересекались, отметим точку, которая поместилась на чертеже. Через эти две точки проведем прямую, которая будет являться серединным перпендикуляром отрезка АВ.
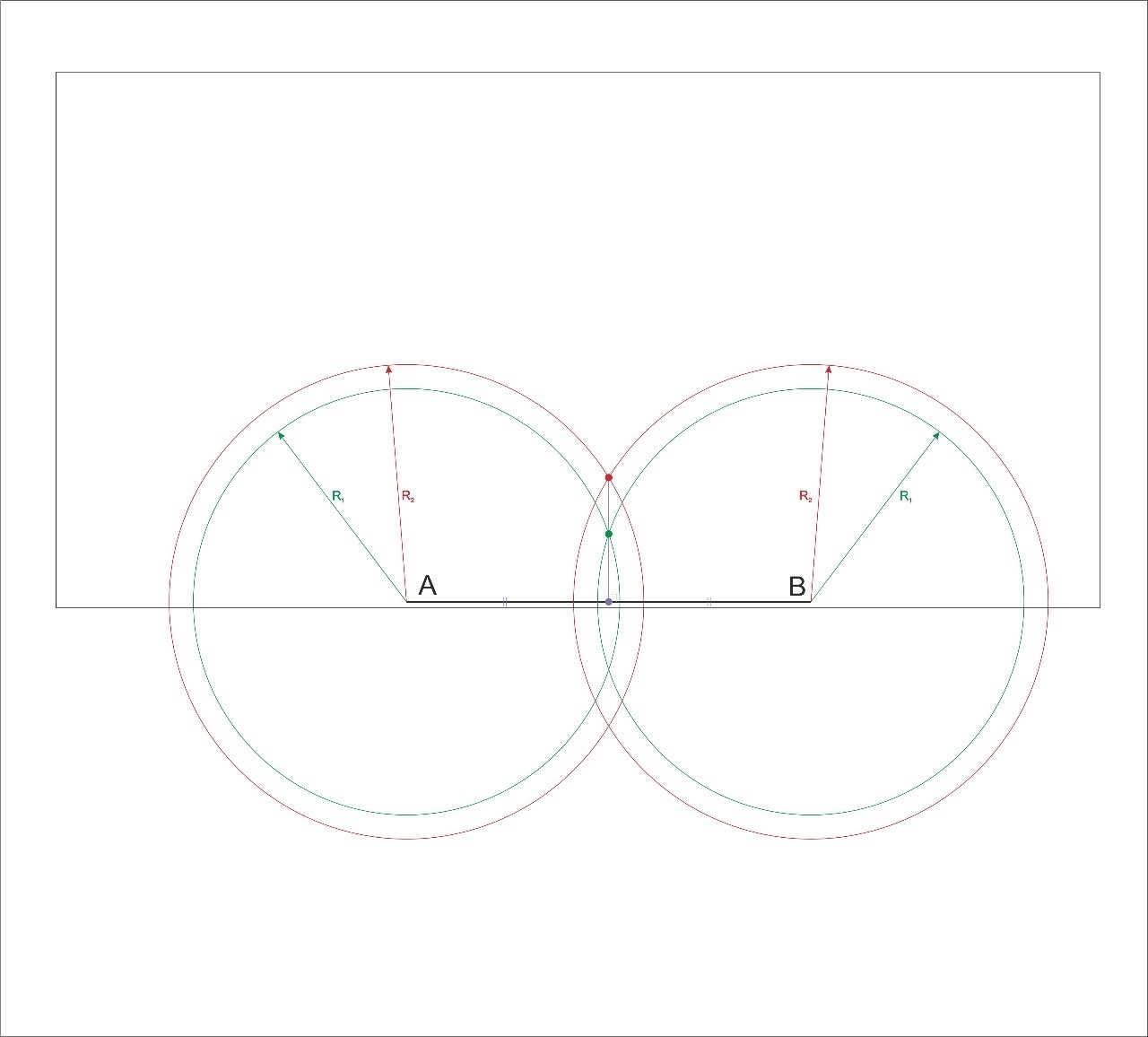
Рисунок 15 - Чертеж к задаче №10
СПИСОК ЛИТЕРАТУРЫ
Асмолов А.Г., Бурменская Г.В., Володарская И.В. и др. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя. – М.: Просвещение, 2011. 159 с.
Концепция развития математического образования в Российской Федерации. Развитие математического образования в Российской Федерации. Министерство образования и науки РФ [Министерство образования и науки Российской Федерации]. Режим доступа: http://минобрнауки.рф/документы/3894.
Макарова Т.А., Елисеева В.П., Патлай А.Л., Марченко А.А. Рабочая программа учебного курса «Геометрия» для 7-9 классов основного общего образования //2022. 90 c.
Мерзляк А.Г. Геометрия: 7 класс: учеб. для учащихся общеобразоват. организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана-Граф, 2015. – 192 с.
Мерзляк А.Г. Геометрия: 8 класс: учеб. для учащихся общеобразоват. организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана-Граф, 2013. – 208 с.
Мерзляк А.Г. Геометрия: 9 класс: учеб. для учащихся общеобразоват. организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана-Граф, 2014. – 240 с.
Подходова Н. С., Панова К. В. Метапредметные учебные задания как средство развития учащихся при обучении математике // Современные проблемы науки и образования. 2016. № 6. URL: https://science-education.ru/ru/article/view?id=25969.
Позднякова Е.В. Математическая деятельность как основа моделирования ключевых универсальных учебных действий учащихся основной школы // Continuum. Математика. Информатика. Образование. – 2022. – № 2 (26). – С. 42-56. doi: 10.24888/2500-1957-2022-2-42-56.
Примерная рабочая программа основного общего образования предмета «Математика», базовый уровень. Одобрена решением федерального учебно-методического объединения по общему образованию, протокол 3/21 от 27.09.2021. Москва, 2021. 104 с.
Примерная рабочая программа основного общего образования предмета «Математика», углубленный уровень. Одобрена решением федерального учебно-методического объединения по общему образованию, протокол 2/22 от 29.04.2022. Москва, 2022. 89 с.
ФГОС ООО [Федеральный государственный образовательный стандарт общего образования]. Министерство образования и науки РФ [Министерство образования и науки Российской Федерации]. Режим доступа: http://минобрнауки.рф/документы/938.
Шкерина Л. В., Гаврилюк А. С., Табинова О. А., Шашкина М. Б. Бипредметный мониторинг результатов освоения универсальных учебных действий обучающимися 7–9 классов в процессе обучения математике // Перспективы науки и образования. 2020. № 2 (44). С. 179-194. doi: 10.32744/pse.2020.2.15.
1







 Анализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC - искомый треугольник: AB = a, AC–BC = AD=d,
Анализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC - искомый треугольник: AB = a, AC–BC = AD=d, 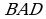 =. Замечаем, что ∆АВD = определен по двум сторонам и углу между ними.
=. Замечаем, что ∆АВD = определен по двум сторонам и углу между ними. 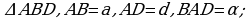

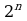 (Например: построение отрезка, являющегося средними геометрическими двух других отрезков.).
(Например: построение отрезка, являющегося средними геометрическими двух других отрезков.).