Сызықтық теңдеулер жүйесі. Крамер формуласы

 Сызықтық теңдеулер жүйесі. Крамер формуласы

1) Сызықтық теңдеулер жүйесін Крамер формуласымен әдісімен шешу

n белгісізді сызықты  n –теңдеулер  жүйесі берілсін (5.1).

(1) теңдеулер  жүйесінің үйлесімді болуының жеткілікті шарты (2)

анықтауышының нөлге тең болмауы. Бұл жағдайда (1) жүйесінің шешуін төмендегі формула арқылы  табады (3):

мұндағы (4)

(3) формуласын  Крамер  формуласы деп атайды.

2) Сызықтық теңдеулер жүйесін матрицалық әдісімен шешу әдісі

Кері матрицаның көмегімен сызықты теңдеулер жүйесін оңай  шешуге болады. (1) жүйесін матрица түрінде жазсақ (6):

мұндағы (7)

егер А- ерекше емес матрица болса, онда (8)

Крамер формуласы бойынша және матрицалық әдіспен сызықты теңдеулер  жүйесін тек мынадай жағдайда ғана шешуге болады:

1.Белгісіздердің саны теңдеулер санына тең болса;

2.Жүйенің анықтауышы нөлге тең  болмаса.

3) Сызықтық теңдеулер жүйесін Жордан – Гаусс әдісімен шешу

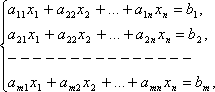
Сызықтық теңдеулер жүйесі берілсін (9)

Осы жүйенің А матрицасынанэлементін аламыз. Бұл элемент шешуші элемент деп, А матрицасының, р-ші тік жолдары – шешуші тік жолдар, q-ші жатық жолдары- шешуші жатық жолдар деп аталады (10).

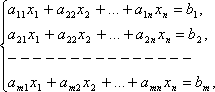
Жаңа теңдеулер жүйесін қарастырамыз. Бұл теңдеулер жүйесінің матрицасы  A`  болады, бұл жүйенің коэффициенттері мен бос мүшелері (11)

формулалардан анықталады. Дербес жағдайда, егер i ≠q. Егерболса, (12)

болады. Олай болса (8) және (9) жүйелеріндегі q-ші теңдеу бірдей, ал (5.9) жүйесінің барлық теңдеулеріндегі  х_р-ң алдыңдағы q-ден басқа барлық коэффициенттер нольге тең.

A` матрицаның элементін анықтау үшін “тіктөртбұрыш ережесін” қолданамыз. А матрицасының өзгеріске ұшырайтын элементін, шешуші элементін және  элементін қарастырамыз. элементін табу үшін   формуласын қолданамыз. Осы баяндалған әдіс Жордан- Гаусс әдісі деп аталады.