Технологическая карта работы над задачей, направленную на формирование универсальных учебных навыков по теме : «Изучение вероятностно-стохастической линии в школьном курсе математики»

Учитель

Петролюк Наталья Александровна

Класс

7

Раздел

Множества

Результаты обучения по разделу

Личностные

Метапредметные

Предметные

-умеют грамотно излагать свои мысли в письменной и устной речи речи;

-понимают смысл поставленной задачи;

-проявляют креативность мышления, находчивость;

- осознают важность и необходимость знаний для человека;

-умеют контролировать процесс и результат своей деятельности.

-умеют видеть математическую задачу в окружающем мире;

-находят различные стратегии решения задач;

-создают алгоритмы для решения математических задач;

- умеют планировать свою деятельность и осуществлять ее.

- умеют выделять множества, подмножества;

- умеют правильно записывать операции над множествами;

- умеют правильно строить круги Эйлера для заданных множеств;

- умеют находить объединение множеств, пересечение множеств, разность множеств аналитическим и графическим способами;

-умеют выполнять устные и письменные вычисления;

- умеют преобразовывать рациональные выражения;

- умеют решать линейные уравнения;

Система задач

Знакомая задача

Малознакомая задача

Незнакомая задача

Заданы два множества: А {2, 3, 4, 5, 6} и В {2, 4, 6, 7, 8}. Определить множество А∩В, АВ, А\В, В\А.

Ответ:

А∩В={2,4,6}

АВ={2,3,4,5,6,7}

А\В={5}

В\А={7}

По данным промежуткам А [4;+∞) и В (2;7] на числовой прямой определить множество А∩В, АВ, А\В, В\А

Ответ:

А∩В=[4, 7]

АВ=(2, ₊∞ ]

А\В=(7;+ ∞]

В\А=(2, 4)

В группе 35 студентов. Каждый из них изучает хотя бы один иностранный язык (английский или французский). Сколько студентов изучает оба языка, если известно, что английский язык изучают 14 человек, а французский – в два раза больше, чем английский.

Ответ: 7

Найдите пересечение и объединение множеств цифр, используемых в записи чисел 15243 и 6321

Ответ:

А∩В={1,2,3}

АВ={1,2,3,4,5,6}

Пересечением каких множеств является а) множество квадратов?; б) множество прямоугольных равнобедренных треугольников

Выполнить решение с помощью кругов Эйлера.

Ответ: а) множества прямоугольников и множества ромбов;

б) множества прямоугольных треугольников и множества равнобедренных треугольников.

В классе 30 человек. 20 из них каждый день пользуется метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?

Ответ: 3

ТЕХНОЛОГИЧЕСКАЯ КАРТА РАБОТЫ НАД ЗАДАЧЕЙ

Формулировка задачи

В классе 30 человек. 20 из них каждый день пользуется метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта.

Решение задачи

Для решения воспользуемся кругами Эйлера:

Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:

20 − (12 − х) − (10 − х) − х = х − 2

Аналогично получаем: 15 – (9 - х) – (12 – х) – х = х − 6 — только автобусом и 23 – (10 - х) – (9 – х) – х = х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:

Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.

х = 3.

Ответ: 3

Основные этапы работы над задачей

Цель этапа

Содержание педагогического взаимодействия

Деятельность учителя

Деятельность учащихся*

Познавательная

Коммуникативная

Регулятивная

Постановка учебной задачи

Создание проблемной ситуации

Предлагает решить задачу (текст в формулировке задачи)

Организовывает «погружение в проблему».

Фиксируют проблему

Слушают учителя и строят речевое высказывания на уточнение задания

Принимают цель

Совместное исследование проблемы

Поиск способов решения задачи

Задает вопросы

- является ли данная задача задачей на множества?

-Какие основные множества можно выделить по условию задачи?

- Будут ли эти множества независимыми друг от друга?

-что нужно сделать, чтобы ответить на вопрос задачи?

Фиксирует ответы учащихся

Отвечают на вопросы:

-да, т.к. можно выделить множества и в дальнейшем выполнить над ними операции согласно условию задачи.

- {М} - множество учащихся, пользующихся метро, {A} – множество учеников, пользующихся автобусом, {Т} – множество учеников, пользующихся троллейбусом.

- нет, так как в классе есть ученики, которые пользуются двумя и даже тремя видами транспорта.

- Нужно выполнить построение кругов Эйлера для заданных множеств и исследовать построенную графическую модель.

Строят грамотно речевые высказывания, слушают высказывания других учащихся, проводят рефлексию своих действий.

Исследуют условия и способы решения задачи

Моделирование

Создание математической модели

Предлагает выполнить построение кругов Эйлера для установленных множеств таким образом, чтобы они удовлетворяли условию задачи

Предлагает составить модели, для нахождения количества учеников, пользующихся:

только М и А;

только Т и А;

только М и Т;

только М;

только А;

только Т

Как, используя полученные данные, найти сколько всего человек пользуется транспортом?

Строят графическую модель показывают на ней связи между множествами, фиксируют известные данные, и приходят к выводу, что нужно найти пересечение всех трёх выделенных множеств: М, А, Т. Количество элементов которого следует обозначить через х.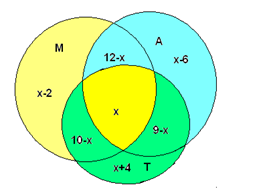

Делают знаково-символическую запись связей и отношений:

Х – кол-во учащихся, пользующихся всеми тремя видами транспорта.

(12 – х) – учеников пользуются только метро и автобусом

(9 – х) – учеников пользуются только троллейбусом и автобусом

(10 – х) – учеников пользуются только метро и троллейбусом

(х – 2) – учеников пользуются только метро;

( х – 6) - учеников пользуются только автобусом;

(х + 4) - учеников пользуются только троллейбусом;

Составляют уравнение:

х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30

Слушают, воспринимают, записывают высказывания

Осуществляют планирование и самоконтроль

Решение задачи

Нахождение решения задачи

Организует решение полученного уравнения, оценивает правильность решения

Решают полученное уравнение:

х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30

х + 12 − х + 9 − х + 10 − х + х + 4 + х − 2 + х − 6 = 30

х + 27 = 30

х = 30 – 27

х = 3

Ответ : 3

Планируют учебное сотрудничество

Осуществляют самоконтроль, коррекцию и самооценку

Интерпретация полученного решения

Ответить на поставленный вопрос

Предлагает дать ответ на вопрос задачи

Отвечают на вопрос задачи: три человека ежедневно пользуются всеми тремя видами транспорта.

Слушают, воспринимают, записывают ответ к задаче

Осуществляют самоконтроль, коррекцию и самооценку

Анализ решения

Оценка рациональности решения

Организует обсуждение рациональности решения и оценивание его

Обсуждают и анализируют решение

Слушают, воспринимают высказывания друг друга , выражают свои мысли.

Осуществляют самоконтроль, коррекцию и самооценку

Контроль

Проконтролировать достижение результата

Дает диагностическую работу по вариантам:

1вариант

В группе 35 студентов. Каждый из них изучает хотя бы один иностранный язык (английский или французский). Сколько студентов изучает оба языка, если известно, что английский язык изучают 14 человек, а французский – в два раза больше, чем английский.

2вариант

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги». Из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Выполняют работу

Рефлексия своих действий

Осуществляют самоконтроль, коррекцию и самооценку