| II | Актуализация опорных знаний
| Разминка (тест) по формулам «Формулы приведения», «Значения синуса, косинуса и тангенса для углов от 0⁰ до 180⁰». См. Приложение 1 Слайд 2
Слайд 3 Проводит фронтальную работу с классом Что изображено на слайде? Ответьте на вопросы: 1.Как называются стороны прямоугольного треугольника? 2.Что называется синусом острого угла прямоугольного треугольника?
3.Что называется косинусом острого угла прямоугольного треугольника? | I. Тест 1) cosα (1) 2) sinα (2) 3) sinα (2) 4) - cosα (3) 5)  (1) (1) 6)  (2) (2) 7)  (3) (3) 8)  (2) (2) 9)  (1) (1) 10)  (3) (3) Отвечают на вопросы учителя На слайде изображен прямоугольный треугольник 1.У прямоугольного треугольника есть 2 катета и гипотенуза 2.Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе. 3.Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе. |
| III | Изучение нового материала
| Слайд 4 Учитель: А. Кларк говорил: «Мало знать, надо и применять. Мало очень хотеть, надо и делать» Перед вами 5 задач на треугольник (4 задачи на прямоугольный треугольник и 1 задача на остроугольный или тупоугольный треугольник), выбирайте любую, решите, защитите. Слайд 5 - 6 Проблемная задача повышает мотивацию учеников на дальнейшую познавательную деятельность. Слайд 7 Организуется ситуация для постановки цели урока и прогнозирования результатов занятия, например, необходимо выяснить универсальный способ нахождения длины третьей стороны треугольника по известным длинам двух других сторон и углу между ними. Объясняет новый материал. Настраивает детей на составление теоретической базы. Слайд 8 В  
4 см ?
 400 400
 А 10 см С А 10 см С
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними
Слайд 9
Доказательство: Внесём в координатную плоскость треугольник ABC. Введём обозначения AB=c, AC=b, CB=a, ∠CAB=α (будем считать что α≠90°). Тогда точка A имеет координаты (0;0), точкаС (b;0).
В (с*cosα;с*sinα)
4 см ?
400 
 А (0;0) 10 см С (b;0) А (0;0) 10 см С (b;0)
Через функцию sin и cos, а также АВ = с выведем координаты точки В (с*cosα;с*sinα). Координаты точки В остаются неизменными при тупом и остром угле α. Зная координаты точек С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:
a2=(b – c*cosα)2+c2sin2α
a2=b2 –2bc*cosα+ c2cos2α+ c2 sin2α= b2 –2bc*cosα+ c2 (cos2α+ sin2α) sin2α =b2 –2bc*cosα+ c2 a2= b2 + c2–2b*cosα
Слайд 10 Стоит отметить, что для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² - теорема Пифагора. А теперь найдите сторону СВ по данной теореме
Ребята, вам предстоит работа в парах. Докажите теорему косинусов через векторы
 
с а

в |
Работают в парах, естественно справляются с 4-мя задачами, с пятой не получается. После защиты простых задач, возникает проблема с решением задачи на не прямоугольный треугольник.
Оформляют решение в тетрадях и на доске
Выполняют чертеж и записи в тетради:
Дано: АВ = 4 см АС = 10 см ∠CAB = 400 Найти: СВ
Решение:
В (с*cosα;с*sinα)
4 см ?
400  
А (0;0) 10 см С (b;0)
a2 = (b – c*cosα)2+c2sin2α a2=b2 –2bc*cosα+ c2cos2α+ c2 sin2α = b2 –2bc*cosα+ c2 (cos2α+ sin2α) sin2α = b2 –2bc*cosα+ c2 a2= b2 + c2–2b* cosα

CB = 116 - 80 * 0,77 CB = 54,4 Ответ: CB = 54,4 (см)
Работа в парах (с дальнейшей взаимопроверкой) Доказательство теоремы через векторы Если стороны а, в, с обозначить соответственно векторами  , ,  и и 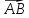 , то справедливо равенство: , то справедливо равенство:  = =  - - 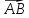
Теперь нужно выполнить некоторые действия. Первое из них — это возведение в квадрат обеих частей равенства:  = =  + +  - 2 - 2  * * 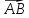
Потом равенство нужно переписать в скалярном виде, учитывая то, что произведение векторов равно косинусу угла между ними на их скалярные значения:  = =  + +  - 2 - 2  * * 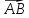 *cosA *cosA
Осталось только вернуться к старым обозначениям, и снова получится теорема косинусов: a2= b2 + c2–2b*cosα |
| IV | Практическая работа в группах
| Учитель задает вопросы. Подготовка к практической работе в группах (определение вида треугольника) 1.Какую задачу можно решать, используя теорему косинусов?
2.Зная, что теорема косинусов имеет вид a2=b2+c2 - 2bc*cosα, преобразуйте данное выражение таким образом, чтобы искомой величиной стал угол α 3.Что можно находить по этой формуле?
Слайд 11
Ученикам предлагается вычислить косинус большего угла в треугольнике с известными длинами трех сторон и определить вид этого треугольника. См. Приложение 2
Результаты вычислений каждой группы заносятся в таблицу, обсуждаются, делаются выводы
Учитель: Как можно ответить на этот вопрос без вычисления косинуса наибольшего угла, используятеорему о соотношении между сторонами и углами треугольника? Теорема: В треугольнике против большей стороны лежит больший угол и, наоборот, против большего угла лежит большая сторона Слайд 12
Учитель: Давайте закрепим наши промежуточные открытия. Сформулируйте теорему косинусов | Отвечают на вопросы учителя:
1.Используя теорему косинусов, можно находить длину третьей стороны по известным двум другим и углу между ними; 2.b2+c2=2bc*cosα+a2 b2+c2- a2 =2bc*cosα cosα= 3.По данной формуле можно найти значение косинуса угла в треугольнике
Практическая работа в группах (определение вида треугольника) с дальнейшей взаимопроверкой
Вывод: Для определения вида треугольника (остроугольный, прямоугольный, тупоугольный)необходимо: 1.Вычислить косинус угла, лежащего напротив большей стороны; 2. Если cosα 0, то треугольник остроугольный; Если cosα = 0, то треугольник прямоугольный; Если cosα
Отвечают на вопрос учителя: Пусть с – наибольшая сторона 1.если с2 2 + b2, то треугольник остроугольный;
2.если с2 = a2 + b2, то треугольник прямоугольный;
3.если с2 a2 + b2, то треугольник тупоугольный.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними |
| V | Закрепление изученного материала
| Учитель: Какие задачи можно решить с помощью теоремы косинусов?
На каждое задание вызывает одного ученика к доске. Остальные ученики выполняют задания в тетради. Слайд 13 № 1025 (е) С помощью теорем синусов и косинусов решите треугольник АВС, если ∠С = 540, а = 6,3, b = 6,3
Учитель задает наводящие вопросы: 1.Что значит, решить треугольник?
2.Какие элементы треугольника нам нужно найти? 3.Как же нам найти сторону треугольника, если известен угол и 2 стороны?
4.Что можно сказать о данном треугольнике по его сторонам?
5.Как найти неизвестные углы в треугольнике?
Самостоятельная работа См. Приложение 3 Слайд 14 | Отвечают на вопросы учителя: С помощью теоремы косинусов можно: 1.находить длину третьей стороны по известным двум другим и углу между ними; 2.определять угол (косинус угла) треугольника по трем известным сторонам 3.определять вид треугольника по трем известным сторонам Один ученик выполняет задание у доски. Остальные ученики выполняют задания в тетради.
№ 1025 (е) С 
А В
Ответы учащегося у доски: 1.Решить треугольник – это значит, по известным его сторонам и углами найти неизвестные его стороны и углы 2.Нам нужно найти ∠В и С, сторону с 3.Сторону с нас можем найти, использовав теорему косинусов
a2= b2 + c2–2b* cosα  = 79,38 - 79,38 * 0,57 = 79,38 - 79,38 * 0,57
 ≈32,72 ≈32,72
с ≈ 5,72
4.Данный треугольник является равнобедренным, так как, а = b = 6,3. По определению равнобедренного треугольника, его углы при основании будут равны, следовательно, ∠А = ∠В 5.По теореме о сумме углов в треугольнике: ∠А = ∠В = (1800 – 540):2 = 630 Ответ: ∠А = ∠В = 630, с ≈ 5,72
Учащиеся выполняют задание самостоятельно (с последующей проверкой) |
| VI | Рефлексия
| Подводит итоги урока. Сегодня мы изучили тему: «Соотношения между сторонами и углами прямоугольного треугольника». А как вы думаете, ребята, как в жизни можно применить теорему косинусов?
Вы совершенно правы! Теорема косинусов активно применяется в жизни. Например, чтоб найти высоту дерева или расстояние до населенного пункта. А узнать, как применяется теорема косинусов в науках – это ваше домашнее задание. Слайд 15 Предлагает ученикам ответить на вопросы. 1.Сегодня на уроке я изучил… 2.Я научился…
3.У меня возникли трудности с…
4.Мне хотелось бы…
Анализирует урок, обосновывает минусы и плюсы работы учащихся. Выставляет отметки в классный журнал. | Подводят итоги урока.
Теорема косинусов очень распространена в инженерии, в строительстве, в науках
Отвечают на вопросы учителя: 1.Сегодня на уроке я изучил теорему косинусов 2. Я научился применять теорему косинусов при решении задач на решение треугольника 3.У меня возникли трудности с самостоятельной работой 4.Мне хотелось бы достичь больших успехов в изучении темы: «Теорема косинусов»
Ученики осознают свои ошибки, проводят самоанализ своей деятельности. |
| VII | Домашнее задание
| Слайд 16 1.§1, п.98.
Выучить теорему косинусов и ее доказательство 2.Решить: № 1025 (ж, з) 3.Творческое домашнее задание: «Придумать жизненную задачу, при решении которой необходимо применить теорему косинусов» 4.Реферат на тему: «Теорема косинусов в науках» (дополнительное домашнее задание, выполняется пожеланию учащихся) |
Получают домашнее задание, записывают его дневник. Анализируют последующий ход работы своей деятельности дома. Задают вопросы учителю по уточнению задания.
Решение домашнего задания См. Приложение 4 |







 (1)
(1) (2)
(2) (3)
(3)

 400
400 А 10 см С
А 10 см С




 ,
,  и
и 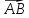 , то справедливо равенство:
, то справедливо равенство: 









