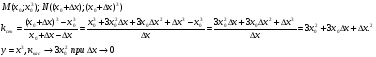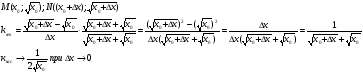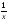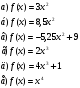Просмотр содержимого документа
«Урок по теме "Производная" 10 класс»
МОБУ «Ленинская средняя общеобразовательная школа № 1 им. П.С.Борисова»
Подготовила:
Учитель математики
Сергеева Ольга Германовна
Ленинский 2012
Урок-лекция по алгебре и началам математического анализа в 10-м классе
по теме: Понятие производной.
Цель урока:
ввести понятие о производной через понятие о касательной к графику функции;
составить таблицу дифференцирования.
Развитие навыков на основе наблюдений делать выводы
Развитие интереса к предмету
Оборудование:
портреты математиков
плакаты с функциями
таблица производных
Ход урока:
Оргмомент
Лекция
Производная родилась от двух родителей:
один из них — Исаак Ньютон (1643-1727), который рассмотрел производную, как физическую величину определения скорости неравномерного движения;
другой — Готфрид Вильгельм Лейбниц (1646-1716), который утверждал, что понятие производной тесно связано с построением касательной к графику функции в заданной точке.
Независимо друг от друга они занимались определением производной (1667-1669).
Мы пойдём путём Лейбница, т.е. от касательной к графику функции.
1. Сформулируем понятие касательной к графику функции в некоторой точке.
Задание 1. Провести касательные к графику функции у= f(х).


Задание 2. Из нескольких прямых выбрать касательную к графику функции у= f(х) в данной точке М.


Вопрос: давайте попробуем дать определение касательной. Что же такое касательная к графику функции в некоторой точке?
Ответ: касательной к графику в некоторой точке называют прямую, которая «хорошо прилипает» к графику той или иной функции в заданной точке.
Научное определение звучит так: Прямую, проходящую через данную точку, практически сливающуюся с графиком функции на определённом отрезке, называют касательной к графику функции в этой точке.
2.Возникает вопрос: как определить точное положение касательной к графику функции в заданной точке.
Вспомним понятие секущей: прямую l, проходящую через любые две точки графика функции, называют секущей.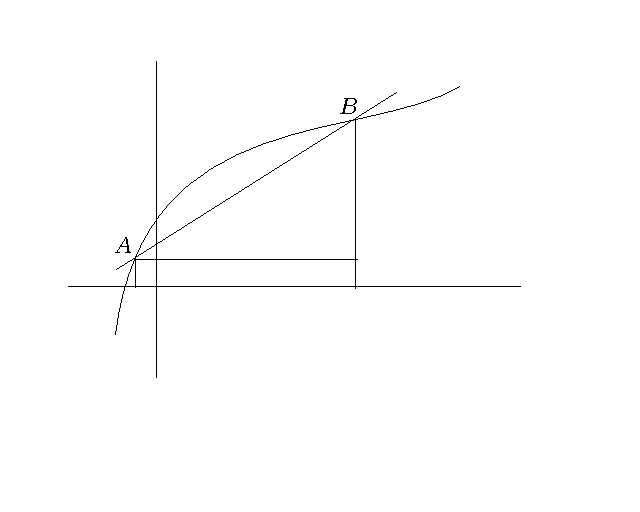
Угловой коэффициент:  ,
, 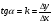
а) рассмотрим функцию y=х2
проведём секущую, проходящую через точки М и N.
М(х0; х02), N (
Найдём угловой коэффициент секущей

MN-секущая, для того, чтобы она стала касательной, точку N приближаем к точке M.
Что происходит с секущей? Она будет поворачиваться, т.е. х уменьшается, а значит х стремится к нулю. А значит 
б) рассмотрим функцию у=2х2
Найдём угловой коэффициент секущей MN:

в) рассмотрим функцию у=2х2+3 и определим угловой коэффициент секущей.
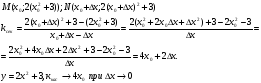
г) рассмотрим функцию у=х3, х R
R
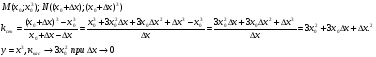
д)рассмотрим функцию 

е) рассмотрим функцию 
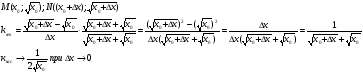
Определение. Производная — есть тангенс угла наклона касательной к графику функции в данной точке к оси абсцисс.
Приведём все полученные формулы в систему, заполнив следующую таблицу.
| f(x) | x2 | 2x2 | 2x2+3 | C | x3 | 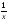
| 
|
| f(x) | 2x | 4x | 4x | 0 | 3x3 | 
| 
|
Определение. Нахождение производной некоторой функции f(х)называется дифференцированием.
3. Закрепление:
Найти производные следующих функций:
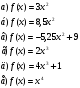
Задание на дом:
Таблица,
Индивидуальные задания на карточках (дифференцированные)
№192, 193 (б,в)












 ,
, 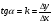




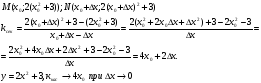
 R
R