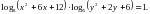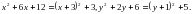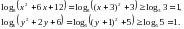1
Урок – семінар
Тема: Використання властивостей функцій для розв’язування рівнянь.
Мета:узагальнити і систематизувати вивчений матеріал з тем « Степенева, показникові і логарифмічна функції»; удосконалити вміння розв’язувати рівняння , обґрунтовано вибираючи одну із стратегій розв’язування ; розвивати вміння і навички розв’язування рівнянь різними методами;
розвивати вміння систематизувати і узагальнювати, робити умовисновки;
виховувати прагнення до реалізації своїх навчальних можливостей.
Клас : 10
Рівняння – це золотий ключ, що відкриває
усі математичні сезами.
С.Коваль
Хід уроку.
І. Організаційний момент.
Мета семінарського заняття полягає в тому, щоб на основі накопичених знань поглибити знання учнів із даних тем.
ІІ. Актуалізація опорних знань.
Клас об’єднано у три команди (по рядах): « Логарифмічна функція»,
« Показникова функція» і « Степенева функція». Кожна команда готувала запитання. За кожну правильну відповідь учень отримує « +» - 1 бал.
Одночасно до дошки викликають двоє учнів для розв’язування практичного завдання.
1. Розв'яжіть рівняння:
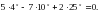
Розв’язання.
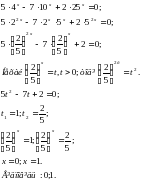
Розв'яжіть рівняння:
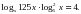
Розв’язання.
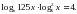

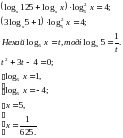

Відповідь: 5;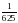
Часто в процесі розв’язування рівнянь буває неможливо скористатися стандартними методами, тоді можна спробувати використовувати властивості функцій. Команди , ставлять питання про властивості функції , яку вони готували.
СТЕПЕНЕВА ФУНКЦІЯ.
1. Дати означення степеневої функції.
2. Вказати область визначення, якщо р- натуральне число.
3. Якщо р- непарне ціле від’ємне число, то в яких координатних чвертях розташований графік?
4. Якщо р = 1/k, де k= 2, 3, 4…. Вказати проміжок зростання функції.
5. Назвати основні методи розв’язування ірраціональних рівнянь.
ПОКАЗНТКОВА ФУНКЦІЯ.
1. Вказати область визначення показникової функції.
2. Яку назву має графік показникової функції?
3. У якій півплощині розміщений графік показникової функції?
4. Через яку точку обов’язково проходить крива функції?
5. Назвати найпоширеніші способи розв’язування показникових рівнянь.
ЛОГАРИФМІЧНА ФУНКЦІЯ,
1. Назвати основну логарифмічну тотожність.
2. Сформулювати основні властивості логарифмів.
3. Вказати область визначення та область значень логарифмічної функції.
4. При якій умові логарифмічна функція зростає?
5.Вказати основні методи розв’язування логарифмічних рівнянь.
.
ІІІ. Систематизація вивченого матеріалу.
Повідомлення учнів.
Функціональні методи розв’язування рівнянь:
1).Застосування скінченої ОДЗ рівняння.
2).Оцінка множини значень лівої та правої частин рівняння.
3).Використання монотонності функцій.
Перший учень:
1) Застосування скінченої ОДЗ рівняння:
якщо область допустимих значень (ОДЗ) рівняння складається із скінченного числа значень, то для розв'язування досить перевірити
всі ці значення.
Розв’яжіть рівняння:

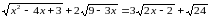
Розв’язання.

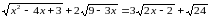
ОДЗ: 
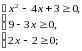
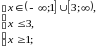
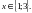
Безпосередньою перевіркою встановлюємо, чи є числа 1 і 3 коренями даного рівняння.
При х =1 маємо: 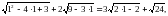 тобто
тобто 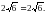 Отже, х =1 – корінь рівняння.
Отже, х =1 – корінь рівняння.
При х =3 маємо: 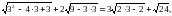 тобто
тобто 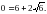 Отже, х =3 – не є коренем рівняння.
Отже, х =3 – не є коренем рівняння.
Відповідь: 1.
Другий учень
2) Оцінка множини значень лівої та правої частин рівняння:
а) Якщо потрібно розв'язати рівняння виду f(x)=g(x) і з’ясувалося, що f(x)≥a, g(x)≤a, то рівність між лівою та правою частинами можлива лише у випадку, якщо одночасно f(x) і g(x) дорівнюють a.
Розв’яжіть рівняння:

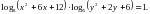
Розв’язання.
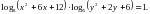
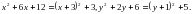
Тоді
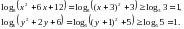
Маємо:

Рівність досягається лише за умови

Відповідь: (-3;-1).
б) Сума кількох невід'ємних функцій дорівнює нулю тоді і тільки тоді, коли всі функції одночасно дорівнюють нулю (рівняння виду  де
де  ).
).
Розв’яжіть рівняння:
(1+)+(1+)=0.
Розв’язання:
(1+)≥0, (1+)≥0.
Маємо:
Звідси : х=0.
Відповідь: х=0.
Розв’язати самостійно:
x²+=1.
Відповідь: х=0.
Третій учень
3) Використання властивості монотонності функцій:
Підбираємо один або декілька коренів рівняння.
Доводимо, що інших коренів це рівняння не має
(використовуючи теореми про корені рівняння).
Теорема І.
Якщо в рівнянні f(x)=a функція f(x) зростає (спадає) на деякому проміжку, то це рівняння може мати не більш ніж один корінь на цьому проміжку.
Теорема ІІ.
Якщо в рівнянні f(x)= g(x) функція f(x) зростає на деякому проміжку,
а функція g(x) спадає на цьому самому проміжку (або навпаки), то це рівняння може мати не більш ніж один корінь на цьому проміжку.
а). Розв’яжіть рівняння:


Розв’язання.
1. Підбором знаходимо, що х =2 - корінь даного рівняння, бо 
2. Доведемо, що інших коренів рівняння не має.
Поділивши обидві частини рівняння на  , одержимо рівносильне рівняння
, одержимо рівносильне рівняння  Розглянемо функцію
Розглянемо функцію  . Ця функція спадна, як сума двох спадних функцій. Отже, відповідно до теореми І, рівняння має не більше, ніж один корінь.
. Ця функція спадна, як сума двох спадних функцій. Отже, відповідно до теореми І, рівняння має не більше, ніж один корінь.
Відповідь: 2.
b). Розв’яжіть рівняння:


Розв’язання.

Нехай  , тоді
, тоді  Маємо рівняння:
Маємо рівняння: 
Розв’яжемо його як квадратне відносно змінної y.




 Останнє рівняння має єдиний розв’язок, оскільки ліва його частина – зростаюча функція, а права – спадна.
Останнє рівняння має єдиний розв’язок, оскільки ліва його частина – зростаюча функція, а права – спадна.
Відповідь: 1; 2.
ІV. Підсумок уроку.
1. Назвіть основні методи розв’язування рівнянь.
2. Які методи ми повторювали сьогодні?
3. Які властивості функцій використовують для розв’язування рівнянь?
V. Домашнє завдання.
Розв’язати рівняння:








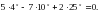
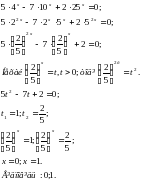
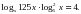
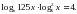

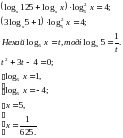

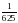
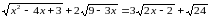
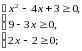
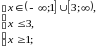
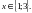
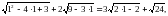 тобто
тобто 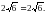 Отже, х =1 – корінь рівняння.
Отже, х =1 – корінь рівняння. 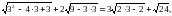 тобто
тобто 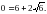 Отже, х =3 – не є коренем рівняння.
Отже, х =3 – не є коренем рівняння.