Урок вероятности в 9 классе. Учитель Гончарова Е.Б.
Тема: «Комбинаторное правило умножения».
Цели: изучить комбинаторное правило умножения; формировать умения решать комбинаторные задачи с помощью правила умножения и составления таблиц возможных вариантов; ввести понятие перестановки из п элементов конечного множества, понятие п!; вывести формулу нахождения числа перестановок с помощью комбинаторного правила умножения и формировать умение ее применения при решении задач.
Ход урока
I. Организационный момент.
II. Проверка усвоения изученного материала.
1. Три друга при встрече обменялись рукопожатиями. Сколько всего было сделано рукопожатий? (3.)
2. Есть помидоры, огурцы и лук. Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей? (3.)
3. Перечислить все возможные способы разложения по двум вазам одного яблока и одной груши. (4.)
4. Сколькими способами Петя и Вова могут занять 2 места за одной двухместной партой? (2.)
5. Сколько подарочных наборов можно составить:
1) из одного предмета; (1.)
2) из двух предметов, если в наличии имеются одна ваза и одна ветка сирени? (3.)
III. Объяснение нового материала.
1. Чтобы подвести учащихся к «открытию» комбинаторного правила умножения, целесообразно начать объяснение нового материала с проверки решения задачи № 714 с выносом графа-дерева решения на доску:

Замечаем, что можно было решить эту задачу даже устно. Рассуждаем так. Первое блюдо можно выбрать двумя способами. Для каждого первого блюда можно подобрать второе четырьмя способами. Эти выборы независимы друг от друга, так как каждый осуществляется из своего множества вариантов. Значит, общее число вариантов обеда равно произведению 2 · 4, то есть 8.
В о п р о с у ч а щ и м с я: а если бы на обед было предложено выбрать еще одно третье блюдо из пяти: чай, кофе, сок, компот, кисель? Тогда для каждого варианта обеда мы могли бы предложить пять вариантов третьего блюда и получили бы 8 · 5 или 40 вариантов обеда из трех блюд.
2. Решая эту задачу, мы использовали так называемое комбинаторное правило умножения.
Формулируем его в общем виде, обращая особое внимание на условие его применения – выбор из независимых наборов вариантов:
Пусть имеется п элементов и требуется выбрать из них один за другим k элементов. Если первый элемент можно выбрать п1 способами, после чего второй элемент можно выбрать п2 способами из оставшихся, затем третий элемент можно выбрать п3 способами из оставшихся и т. д., то число способов, которыми могут быть выбраны все k элементов, равно произведению п1 · п2 · п2 · … · пk.
3. П р и м е р 3 рассматриваем из учебника со с. 185.
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
З а д а ч а. В комнате вдоль стены стоят шкаф (ш), стол (с), кресло (к). Мама решила сделать перестановку мебели. Сколько вариантов расположения этих трех предметов мебели существует?
Опять нацеливаем ребят на то, что надо не произвольно называть варианты, а выработать стратегию, алгоритм перечисления, перестановок:
1-й ш а г. Фиксируем первый элемент – шкаф, дописываем к нему два возможных выбора из двух оставшихся элементов:
ш – с – к; ш – к – с.
2-й ш а г. Фиксируем второй элемент – стол, дописываем к нему два возможных выбора из двух оставшихся элементов:
с – ш – к; с – к – ш.
3-й ш а г. Фиксируем третий элемент – кресло, дописываем к нему два возможных выбора из двух оставшихся элементов:
к – ш – с; к – с – ш.
И т о г о – 6 вариантов расположения мебели (один из которых является исходным).
Каждое из возможных таких расположений трех элементов называют перестановкой из трех элементов.
Далее формулируем определение:
Перестановкой из п элементов называется каждое расположение этих элементов в определенном порядке.
Обозначение: Рп (читается «Р из п»).
Затем замечаем, что для подсчета количества перестановок можно воспользоваться комбинаторным правилом умножения, тогда
Рп = п (п – 1) (п – 2) · … · 3 · 2 · 1
или Рп = 1 · 2 · 3 · … (п – 2) (п – 1) · п
| 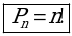 | , где п! – произведение первых п натуральных чисел (читается «п факториал!»), по определению 1! = 1 |
IV. Формирование умений и навыков.
№ 728.
В задаче 4 последовательных выбора, каждый из своего множества вариантов. Общее количество различных карнавальных костюмов равно:
5 · 6 · 3 · 2 = 180.
О т в е т: 180 различных костюмов.
№ 732, № 735. Несмотря на то, что эти упражнения очень просты, важно не допустить формального применения учащимися формулы! Обязательно проводить анализ условия и обосновывать, что речь в задаче идет именно о числе перестановок.
№ 732.
Р е ш е н и е
Количество человек равно количеству мест на скамейке, поэтому количество способов размещения равно числу перестановок из 4 элементов:
Р4 = 4! = 1 · 2 · 3 · 4 = 24.
О т в е т: 24 способами.
В № 735 важно правильно понять вопрос задачи, тогда всего перестановок Р5 = 5! = 120, но выражений 119, так как исходное выражение не рассматриваем.
№ 736.
Р е ш е н и е
Три последние цифры телефонного номера могут быть расположены в одном из Р3 = 3! = 6 возможных порядков, из которых только один верный. Наибольшее число вариантов Ольге придется набрать, если правильный ответ окажется последним, то есть шестым.
О т в е т: 6 вариантов.
№ 737 (б).
Р е ш е н и е
Так как число шестизначное, следовательно, нуль не может стоять на первом месте. Задачу можно решить двумя способами:
I с п о с о б. Применим комбинаторное правило умножения: на первое место можно выбрать любую цифру из пяти (кроме нуля); на второе – любую из пяти оставшихся (нуль входит); на третье – любую из четырех оставшихся после первых двух выборов цифр и т. д. Общее количество вариантов равно:
5 · 5 · 4 · 3 · 2 · 1 = 600.
II с п о с о б. Метод исключения лишних вариантов.
Из 6 цифр можно сделать перестановок Р6 = 6! = 720, но в этом случае будут варианты с нулем на первом месте, их и надо исключить.
Если нуль на первом месте (фиксирован), то количество способов размещения оставшихся пяти цифр на пяти местах равно Р5 = 5! = 120.
Искомое количество шестизначных чисел в этом случае равно
Р6 – Р5 = 720 – 120 = 600.
О т в е т: 600 чисел.
№ 738.
Р е ш е н и е
Фиксируем цифру 3 на первом месте; тогда на трех оставшихся местах в произвольном порядке могут располагаться цифры 5, 7, 9. Число вариантов равно Р3 = 3! = 6.
О т в е т: 6.
№ 748 (а, в, г).
Р е ш е н и е
а) 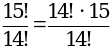 = 15;
= 15;
г) 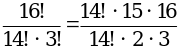 = 40.
= 40.
V. Итоги урока. Рефлексия.
В о п р о с ы у ч а щ и м с я:
– Какие способы решения комбинаторных задач вы знаете?
– Охарактеризуйте каждый способ решения.
– Сформулируйте комбинаторное правило умножения.
– Что означает запись п!?
– Что называется перестановкой из п элементов?
– Запишите формулу для вычисления числа перестановок из п элементов.
Домашнее задание: п. 30, 31 № 733, № 734, № 738 (б), № 746 (б, г), № 748 (б, д, е).
Подготовка к ОГЭ.






















