проверить уровень математической подготовки учащихся 11 класса с позиций Единого Государственного экзамена.
Входная контрольная работа по математике в 11 классе рассчитана на два астрономических часа. Контрольная работа содержит 12 заданий базового уровня, требующих краткого ответа, и 3 задания повышенного уровня, для которых следует привести полное решение. Задания соответствуют структуре заданий демонстрационной версии ЕГЭ 2020. К каждому заданию требуется дать краткий ответ, представленный в виде целого числа, промежутка и конечной десятичной дроби.
Каждое задание первой части оценивается одним баллом. Во второй части каждое задание – два балла. Вся работа оценивается 18 баллами.
| ВХОДНАЯ КОНТРОЛЬНАЯ РАБОТА
ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 11 КЛАССЕ
|
| ВХОДНАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 11 КЛАССЕ
ВАРИАНТ I
|
| 1 | Таксист за месяц проехал 6000 км. Стоимость 1 литра бензина 20 рублей. Средний расход бензина на 100 км составляет 9 л. Сколько рублей потратил таксист на бензин за этот месяц?
|
| 2 | На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года. Ответ дайте в градусах Цельсия. 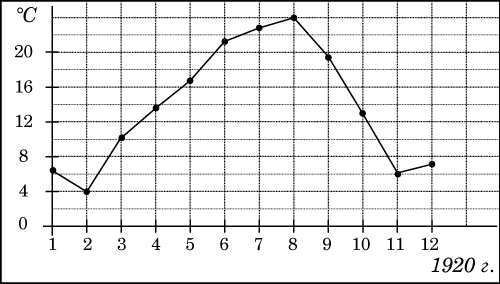
|
| 3 | Поступивший в продажу в январе мобильный телефон стоил 2400 рублей. В ноябре он стал стоить 1200 рублей. На сколько процентов снизилась цена на мобильный телефон в период с января по ноябрь? |
| 4 | В чемпионате по гимнастике участвуют 75 спортсменок: 15 из Чехии, 30 из Словакии, остальные – из Австрии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Австрии. |
| 5 | Найдите корень уравнения: 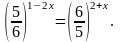 |
| 6 | В треугольнике ABC угол A равен 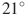 , угол B равен , угол B равен 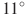 . AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. . AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. |
| 7 | Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ А) площадь почтовой марки 1) 362 кв. м Б) площадь письменного стола 2) 1,2 кв. м В) площадь Санкт-Петербурга 3) 1439 кв. км Г) площадь волейбольной площадки 4) 5,2 кв. см В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
Ответ:
|
| 8 | Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 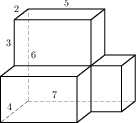
|
| 9 | Найдите значение выражения 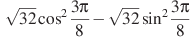 . . |
| 10 | Расстояние от наблюдателя, находящегося на небольшой высоте 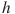 километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле 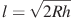 , где , где 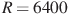 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 136 километров? Ответ выразите в километрах. (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 136 километров? Ответ выразите в километрах. |
| 11 | От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч. |
| 12 | В прямоугольном параллелепипедеABCDA1B1C1D1 известно, что BB1=19, CD=16, BC=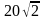 . Найдите длину отрезка MK, где M– середина ребра DC, K – середина ребра A1D1. . Найдите длину отрезка MK, где M– середина ребра DC, K – середина ребра A1D1. |
| 13 | а) Решите уравнение: cos2x-3cosx=-2 б) Укажите корни, принадлежащие отрезку 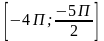 . . |
| 14 | Решить систему уравнений: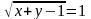 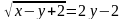
|
| 15 | Решить неравенство: 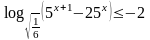 |
| ВХОДНАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 11 КЛАССЕ
ВАРИАНТ II
|
| 1 | Таксист за месяц проехал 6000 км. Стоимость 1 литра бензина 23 рублей. Средний расход бензина на 100 км составляет 8 л. Сколько рублей потратил таксист на бензин за этот месяц? |
| 2 | На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену никеля на момент закрытия торгов в период с 7 по 15 мая (в долларах США за тонну). |
| 3 | Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 13000 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях. |
| 4 | В соревнованиях по толканию ядра участвуют 6 спортсменов из Великобритании, 3 спортсмена из Франции, 6 спортсменов из Германии и 10 – из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции. |
| 5 | Найдите корень уравнения: |
| 6 | В треугольнике ABC угол A равен  , угол B равен , угол B равен  . AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. . AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. |
| 7 | Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ А) объём комнаты 1) 78 200  Б) объём воды в Каспийском море 2) 75  В) объём ящика для овощей 3) 50 л Г) объём банки сметаны 4) 0,5 л В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения. Ответ:
|
|
8 | Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
| 9 | Найдите значение выражения . |
| 10 | Расстояние от наблюдателя, находящегося на небольшой высоте 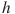 километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле 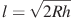 , где , где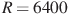 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии четыре километра? Ответ выразите в километрах. (км) — радиус Земли. С какой высоты горизонт виден на расстоянии четыре километра? Ответ выразите в километрах. |
| 11 | На изготовление 99 деталей первый рабочий затрачивает на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает первый рабочий? |
| 12 | Длины сторон прямоугольника равны 8 и 6 см. Через точку O пересечения его диагоналей проведена прямая ОK, перпендикулярная его плоскости. Найдите расстояние от точки K до вершин прямоугольника, если ОK=12 см. |
| 13 | а) Решите уравнение 2cos х = х =  sin( sin( – x). – x). б) Укажите корни, принадлежащие отрезку  . .
|
| 14 | Решить систему уравнений:  |
| 15 | Решить неравенство: |








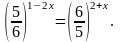

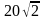 . Найдите длину отрезка MK, где M– середина ребра DC, K – середина ребра A1D1.
. Найдите длину отрезка MK, где M– середина ребра DC, K – середина ребра A1D1.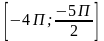 .
.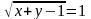
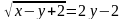
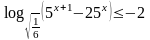
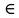 Z;
Z; 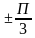 +2Пк, к
+2Пк, к 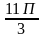 .
.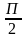 + Пк, к
+ Пк, к 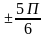 +2Пк, к
+2Пк, к 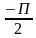 ;
; 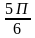 .
.









