Выступление на РМО по теме:"Проблемы преемственности в преподавании математики между начальной школой и 5 классом"

МБОУ Орловская СОШ

ВЫСТУПЛЕНИЕ НА РМО

Проблемы преемственности в преподавании математики между начальной школой и 5 классом.

Возможные пути их решения.

Подготовила: учитель начальных классов

I квалификационной категории

Афанасьева Юлия Петровна

Орловка 2016 г

Проблемы преемственности в преподавании математики между начальной школой и 5 классом

и возможные пути их решения. (слайд №1)

Наблюдения в школе за характером изме­нений в подготовленности и развитии вы­пускников начальных классов в последние годы свидетельствуют о наличии ряда дос­таточно распространенных проблем, сказы­вающихся на успешности усвоения ими курса математики на начальном этапе.

При изучении школьного курса математики, как и при строительстве любого здания, важен основательный, прочный фундамент, иначе, каким бы ни было дальнейшее строительство, здание не будет устойчивым. (слайд №2) Но и на прочном фундаменте можно возвести хлипкое сооружение. Потому и пути решения проблем преемственности между отдельными ступенями школы, в том числе и в школьном курсе математики, «двусторонние». С одной стороны, необходимо обеспечить достаточное общее и специальное математическое развитие учеников в начальных классах. А с другой, чтобы ученикам было легче адаптироваться к новым условиям, очень важно учителю начать обучение предмету с использованием тех методических приёмов, которыми пользуются учителя начальной школы. (слайд №3) Ведь если посмотреть на материал, который изучается в пятом классе, то видно, что он большей частью является обобщением тех знаний, с которыми учащиеся пришли из начальной школы.

Между учителем начальной школы и учителем основной школы возникают трения. Мы часто слышим основные «претензии» к учителю начальной школы в том, что учащиеся 4 класса не умеют :

• применять теорию для решения практических задач,

• не могут выразить свою мысль математическим языком,

• имеют слабые вычислительные навыки,

• плохо знают компоненты арифметических действий,

• не умеют решать типовые задачи.

Учителя начальной школы в свою очередь «укоряют» своих коллег основного звена за :

• излишне строгие требования, предъявляемые учащимся на первых уроках, не знание программ, учебников и методов работы начальной школы,

• а так же за то, что не учитывают возрастные особенности младших школьников.

Всё перечисленное приводит к проблемам преемственности, к резкому снижению успеваемости, потере интереса к предмету. Давно сделан основополагающий вывод: проблему преемственности можно решить только совместными усилиями учителей начальной и основной школы.

Обсуждая проблему преемственности, обычно выделяют содержание учебного материала предыдущего класса, которое нужно помнить к началу следующего года.

Предлагаю ознакомиться с принципом непрерывности, обеспечивающим преемственные связи на уровне содержания (слайд №4,5,6)

Важнейшее условие, позволяющее правильно строить учебный процесс, сделать обучение эффективным, доступным, заключается в том, чтобы в каждой теме выделять главные стороны, исходя из этого чётко дифференцировать материал: вычленять те задачи, которые должны отрабатываться и выполняться многократно, и те, которые служат другим целям (развитию познавательных интересов) и в соответствии с этим не должны дублироваться. Такое различие следует сделать явным и для самих учащихся. В первой четверти пятого класса необходимо повторять те вопросы, знание которых должно быть доведено до автоматизма. (слайд №7)

1. Это счёт (в том числе и обратный) десятками, сотнями и т.п., таблицы сложения и умножения однозначных чисел, тренировка памяти на удержание в уме промежуточных результатов вычислений (36:9+ 77:7).

2. Подбор примеров для повторения письменных алгоритмов выполнения арифметических действий должен провести учеников от простых случаев, включающих собственно умение выполнять алгоритм, до сложных- с постепенным увеличением числа «запоминаний» и «заниманий» единицы.

3. Решение текстовых задач составляет значительную часть деятельности школьников при изучении математики.

Усвоение материала будет более эффективным, если опираться на особенности соотношения конкретного и абстрактного мышления данного контингента учащихся. В соответствии с этим на уроках умственная деятельность должна подкрепляться конкретной материальной деятельностью. Значительное место при изучении геометрического материала в моей работе занимают упражнения, в которых требуется начертить, перерисовать, измерить. Это позволяет стимулировать развитие наглядно-действенного мышления у детей и на его основе в дальнейшем - образного мышления.

Серьёзное внимание уделяю развитию общеучебных умений учащихся. Так, например, формирую навыки самоконтроля, то есть обучаю школьников приёмам проверки своих действий. Задания типа « как проверить решение задачи, выражения» являются постоянными вопросами на уроках.

Ещё одно условие, выполнение которого помогает развитию продуктивной мыслительной деятельности - это систематическое решение нестандартных задач. Подчеркнём, что решение задач такого рода является обязательным элементом методической системы, так как при этом учащиеся овладевают разнообразными приёмами мыслительной деятельности.

Младший школьник, как известно, не обладает достаточным уровнем абстрактного мышления. Поэтому при решении текстовой задачи у четвероклассников возникают трудности в её осмыслении, и, следовательно, в решении. Решение задач провожу с помощью графических моделей и чертежей, которые позволяют младшему школьнику наиболее полно и конкретно представить текст задачи и, что самое важное, даёт реальную возможность наглядно увидеть и определить алгоритм её решения, осуществить самостоятельно рефлексию выполненного задания.

Одной из важнейших задач начального обучения всегда было и остаётся формирование сознательных и прочных (во многих случаях доведенных до автоматизма) навыков вычислений. Одно из условий успешного обучения учащихся в старших классах - хорошо развитые навыки устного счёта. В устных вычислениях развиваются память учащихся, быстрота их реакции, сосредоточенность. К тому же, хорошо известно, что учащиеся, владеющие твердыми навыками устного счета, быстрее овладевают технику алгебраических преобразований, лучше справляются с различными заданиями, составной частью которых являются вычисления.

На своих уроках уделяю особое внимание этому виду работы. Для этого использую различные виды упражнений для устного счёта: (слайд №8)

• беглый слуховой счёт (арифметические (математический) диктанты)

• зрительный счёт (таблицы, плакаты, записи на доске, тесты, презентации)

• комбинированный счёт ( показ ответов с помощью карточек, математические игры «Молчанка», «Да -нет» и т.д.)

Четвероклассники часто испытывают затруднения при выполнении арифметических вычислений в выражениях сложной структуры – несколько скобок, много арифметических действий. Помочь в ликвидации ошибок учеников может графическая блок-схема выражения. После записи примера в несколько действий начинаем вычисления с выделения отдель­ных блоков, из которых он состоит, обра­щаем внимание на знаки арифметических действий, а затем на порядок выполнения арифметических действий.

От того насколько прочен процесс формирования вычислительных навыков в начальной школе, насколько глубок и разнообразен подход при формировании математических способностей, во многом зависит успех дальнейшего обучения математике.

В числе разнообразных и эффективных методов обучения математике особое место занимает метод, состоящий в использовании различного рода наглядных опорных схем, таблиц, памяток. При этом дети овладевают не только математическими знаниями, но и приобретают умения самостоятельно их использовать. Памятки-подсказки собираем не только в личном сборнике ученика, но и самые основные выносятся на обложку тетради по математике. Опора на памятку позволяет ученику правильно организовать вычислительную работу, быстро систематизировать знания, развивает внимание, умение находить и исправлять допущенные ошибки (слайд№9)

Для развития интереса к математике повышения уровня подготовки наиболее способных учащихся в нашей школе ежегодно проводятся олимпиады, дети принимают участие в международном конкурсе “Кенгуру”

Учащиеся 5 класса занимаются по учебнику Математика 5 класс авторов Г. К. Муравина. (слайд№10)

Проанализировав данный учебник, выяснила, что теоретический материал изучается небольшими блоками. Учебник содержит много интересных фактов из географии, истории, биологии, техники. Каждый пункт завершается вопросами и заданиями для самоконтроля. Задачи дифференцированы по уровню трудности, к большинству  из них даны ответы, а к трудным задачам - советы и решения. В учебник включены дополнительные материалы: сведения из истории математики, предметный указатель, список дополнительной литературы и интернет-ресурсы,  практикумы: вычислительный, геометрический, по решению текстовых задач, по развитию пространственного воображения. В учебнике изложен материал, представленный заданиями различной сложности, исследовательскими и домашними контрольными работами. В учебнике предусмотрена система дополнительных заданий для талантливых детей.

Для планирования своей работы посещаю уроки математики в 5-м классе, особенно в начале года, изучаю программу 5-го класса, чтобы знать, какая необходима конкретная подготовка, какие вопросы отрабатываются в начале года в 5-м классе, вношу соответствующие корректировки в свою работу. Учителю начальных классов необходимо знать темы, которые вызывают наибольшие затруднения у пятиклассников.

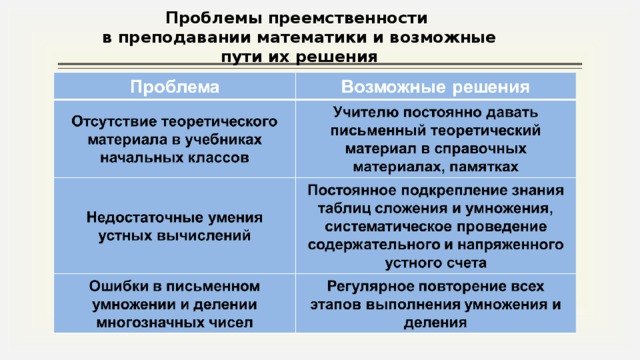
Хочется отметить некоторые проблемы преемственности в преподавании математики между начальной школой и 5 классом (слайд №11,12)

И это далеко не полный список проблем преемственности в преподавании математики между начальной школой и 5 классом. В нашей школе разработана программа преемственности между начальной и средней ступенями обучения.

На основании опыта своей работы выработала общие рекоменда­ции учителям начальных классов. (слайд №13)

1. Уменьшить долю фундаментальных бесед и других малоэффективных методов работы на уроках, использовать раздаточ­ный дидактический материал.

2. Приучить школьников начинать ра­ботать на уроке по звонку, быстро вклю­чаться в выполнение заданий, не давать отдельным ученикам дополнительного времени на выполнение контрольных и проверочных работ, заканчивать урок так­ же со звонком.

3. Постоянно предлагать учащимся за­дания на проверку знаний и понимание смысла математических терминов, вести словарики терминов, читать вслух и анали­зировать условия задач.

4. Уделить особое внимание формиро­ванию навыка табличного сложения и ум­ножения, систематически проводить содержательный и напряженный устный счет.

5. Регулярно повторять все этапы алго­ритма выполнения деления, систематиче­ски включать в устную работу задания на табличное умножение и деление, сложение и вычитание.

6. Предлагать сначала представить се­бе ситуацию, о которой идёт речь в задаче, а за­ тем попробовать изобразить ее на рисун­ке или схеме. Систематически на уроках решать нестандартные задачи, задачи на логику и сообразительность, которые помогают развитию продуктивной мыслительной деятельности.

7. Предлагать учащимся задания по работе со справочниками и словарями, поручать готовить сообщения, расска­зы, сочинения по дополнительным мате­риалам.

Внедрение данных рекомендаций в учебный процесс будет способствовать стабилизации качественных показателей при переходе учащихся в основную школу и как следствие – рост уровня удовлетворённости школьной жизнью и успешной адаптации выпускников начальной школы в пятых классах.

Организация работы по преемственности во многом облегчает переход на новые ФГОС,  активизирует  методическую работу, обнаруживает скрытые резервы коллектива школы. В нашей школе маленький педагогический коллектив, который сформировался много лет назад. Мы тесно сотрудничаем друг с другом. Проводятся регулярные обсуждение успехов и возникающих трудностей, обмен опытом, коллективная выработка способов преодоления трудностей учителей предметников и учителей начальных классов

Итак, для успешного решения проблемы преемственности на современном этапе необходимо: (слайд№14)

• полностью согласовать требования к математической подготовке учащихся, сформулированные в программах начальной и основной школы;

• согласовать методы обучения, обеспечивающие достаточную подготовку учащихся младших классов к восприятию обобщенных фактов, правил, законов, адаптацию школьников к дедуктивному методу изложения;

• строить обучение математике так, чтобы достижение учащимися обязательных результатов обучения было безусловным требованием и непременно контролировалось;

• выявить опорные умения для смежных дисциплин;

• сгладить переход от одного учителя ко многим учителям-предметникам;

• создать оптимальные условия для реализации системы средств обучения, разработать комплекс учебных пособий.

• установить тесную связь в методах работы с учащимися между учителями 4-х и 5-х классов.

Рассмотрение математических проблем преемственности позволяет мне, как учителю начальной школы, скорректировать программу обучения с целью пропедевтического изучения отдельных тем в младших классах, а также позволит продолжить работу в средней школе, учитывая методические приёмы учителя первой ступени обучения. Изучение проблем преемственности помогает увидеть перспективу тех математических знаний, умений, которые формирует учитель и на этой основе осуществлять связь с дальнейшим обучением математике.

Современная школа может выполнять работу по преемственности лишь в том случае, если будут осуществляться все направления преемственности в едином образовательном процессе, в тесном взаимодействии начальной и основной школы. (слайд №15)

Только целостный педагогический процесс обеспечит ребенку условия, при которых он в переходный период будет чувствовать себя комфортно, будет ощущать себя востребованной личностью.

Проблемы преемственности

в преподавании математики

между начальной школой

и 5 классом.

Возможные пути их решения.

Подготовила: учитель начальных классов МБОУ Орловской СОШ

Афанасьева Ю.П.

При изучение школьного курса

важен прочный и основательный фундамент

Необходимо обеспечить общее и специальное математическое развитие учеников в начальных классах

Очень важно учителю начать обучение предмету с использованием тех методических приёмов, которыми пользуются учителя начальной школы

Принцип непрерывности, обеспечивающий преемственные связи на уровне содержания.

Планируемые результаты

5-й класс

• Выполнять устно сложение, вычитание, умножение и деление однозначных, двузначных и трёхзначных чисел в случаях, сводимых к действиям в пределах 100 (в том числе с нулём и числом 1); вычислять значение числового выражения (содержащего 2—3 арифметических действия, со скобками и без скобок).

• Продолжается работа не только с натуральными, но и дробными числами; совершенствуются практических навыков выполнения устных, письменных, инструментальных вычислений, вычислительной культуры;

2. Выделять неизвестный компонент арифметического действия и находить его значение;

2. Продолжается решение уравнений. Уточняются понятия уравнения и корня уравнения. Решение уравнений с преобразованием выражений (раскрытие скобок, приведения подобных слагаемых

3. Решать арифметическим способом (в 1—2 действия) учебные задачи и задачи, связанные с повседневной жизнью

3. Повторяются и систематизируются все изученные учащимися виды текстовых задач, причем задачи предлагаются с различными «ловушками»: несоответствие единиц, неполные данные, нереальные условия и т.д.

4. Измерять длину отрезка; вычислять периметр треугольника, прямоугольника и квадрата, площадь прямоугольника и квадрата;

4. Продолжается работа по измерению длины отрезков, величины углов, использованию формулы для нахождения периметров, площадей и объемов простейших геометрических фигур (прямоугольный параллелепипед, куб);

5. Решать задачи на нахождение доли величины и величины по значению её доли (половина, треть, четверть, пятая, десятая часть);

5. Продолжается работа с обыкновенными дробями, начатая в 4-ом классе. Расширяется аппарат действий с дробями используется в дальнейшем для решения текстовых задач.

6. Читать несложные готовые таблицы;

заполнять несложные готовые таблицы;

6. Продолжается работа по представлению данных в виде таблиц, диаграмм,

читать несложные готовые столбчатые диаграммы.

чтение информации, представленной в виде таблицы, диаграммы.

В первой четверти пятого класса необходимо повторять

• Счёт (в том числе и обратный) десятками, сотнями, тысячами, таблицы сложения и умножения однозначных чисел, тренировка памяти на удержание в уме промежуточных результатов вычислений (36:9+ 77:7).
• Подбор примеров для повторения письменных алгоритмов выполнения арифметических действий должен провести учеников от простых случаев, включающих собственно умение выполнять алгоритм, до сложных- с постепенным увеличением числа «запоминаний» и «заниманий» единицы.
• Решение текстовых задач составляет значительную часть деятельности школьников при изучении математики.

Упражнения для устного счёта:

• беглый слуховой счёт (арифметические (математический) диктанты)
• зрительный счёт (таблицы, плакаты, записи на доске, тесты, презентации)
• комбинированный счёт ( показ ответов с помощью карточек, математические игры «Молчанка», «Да -нет»)

Использовании наглядных опорных схем, таблиц, памяток.

Математика 5 класс авторов Г. К. Муравин, О.В. Муравина

• содержит много интересных фактов из географии, истории, биологии, техники

• каждый пункт завершается вопросами и заданиями для самоконтроля.

• задачи дифференцированы по уровню трудности

• включены дополнительные материалы: сведения из истории математики, предметный указатель, список дополнительной литературы и интернет-ресурсы, практикумы: вычислительный, геометрический, по решению текстовых задач, по развитию пространственного воображения.

• изложен материал, представленный заданиями различной сложности, исследовательскими и домашними контрольными работами.

• предусмотрена система дополнительных заданий для талантливых детей.

Проблемы преемственности

в преподавании математики и возможные пути их решения

Общие рекомендации учителям начальных классов.

1. Уменьшить долю фундаментальных бесед и других малоэффективных методов работы на уроках, использовать раздаточный дидактический материал.

2. Приучить школьников начинать работать на уроке по звонку, быстро включаться в выполнение заданий, не давать отдельным ученикам дополнительного времени на выполнение контрольных и проверочных работ, заканчивать урок так¬ же со звонком.

3. Постоянно предлагать учащимся задания на проверку знаний и понимание смысла математических терминов, вести словарики терминов, читать вслух и анализировать условия задач.

4. Уделить особое внимание формированию навыка табличного сложения и умножения, систематически проводить содержательный и напряженный устный счет.

5. Регулярно повторять все этапы алгоритма выполнения деления, систематически включать в устную работу задания на табличное умножение и деление, сложение и вычитание.

6. Предлагать сначала представить себе ситуацию, о которой идёт речь в задаче, а за¬ тем попробовать изобразить ее на рисунке или схеме. Систематически на уроках решать нестандартные задачи, задачи на логику и сообразительность, которые помогают развитию продуктивной мыслительной деятельности.

7. Предлагать учащимся задания по работе со справочниками и словарями, поручать готовить сообщения, рассказы, сочинения по дополнительным материалам.

Для успешного решения проблемы преемственности на современном этапе необходимо:

• полностью согласовать требования к математической подготовке учащихся, сформулированные в программах начальной и основной школы;

• согласовать методы обучения, обеспечивающие достаточную подготовку учащихся младших классов к восприятию обобщенных фактов, правил, законов, адаптацию школьников к дедуктивному методу изложения;

• строить обучение математике так, чтобы достижение учащимися обязательных результатов обучения было безусловным требованием и непременно контролировалось;

• выявить опорные умения для смежных дисциплин;

• сгладить переход от одного учителя ко многим учителям-предметникам;

• создать оптимальные условия для реализации системы средств обучения, разработать комплекс учебных пособий.

• установить тесную связь в методах работы с учащимися между учителями 4-х и 5-х классов.

Современная школа может выполнять работу по преемственности лишь в том случае, если будут осуществляться все направления преемственности в едином образовательном процессе, в тесном взаимодействии начальной и основной школы.

Спасибо за внимание !