|
1. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
|
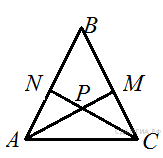
2 В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите  . .

|
|
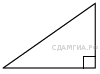
3. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 12 и 13.

|
4.  Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите  , если , если  , а , а 
|
|
5. Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

|
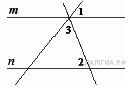
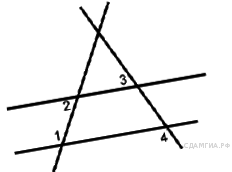
6. Прямые m и n параллельны. Найдите угол 3, если угол 1 равен 24°, угол 2 равен 76° . Ответ дайте в градусах.

|
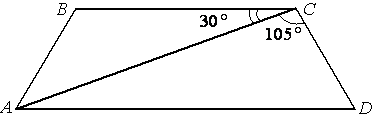
- Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.

|
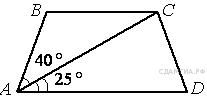
- Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.

|
|
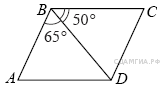
9. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.

|
10. В трапеции ABCD AB = CD, угол BDA равен 49° и угол BDC равен 13°. Найдите угол ABD. Ответ дайте в градусах.

|
|
11. В треугольнике ABC угол C равен 90°, BC = 6, sin A = 0,3. Найдите AB.

|
12. Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
|
|
13. В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
|
14. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BCугол, равный 15°. Ответ дайте в градусах.

|
|
15. На плоскости даны четыре прямые. Известно, что  , ,  , ,  . Найдите . Найдите  . Ответ дайте в градусах. . Ответ дайте в градусах.

|
16. В прямоугольном треугольнике  катет катет  , а высота , а высота  , опущенная на гипотенузу, равна , опущенная на гипотенузу, равна  Найдите Найдите 
|
|
17. У треугольника со сторонами 12 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
|
18. Площадь прямоугольного треугольника равна  Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу. Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.
|
|
19. Задание 9 № 340864. В треугольнике ABC угол A равен 90°, AC = 6, sinB = 0,3. Найдите BC.

|
20. На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 44°. Найдите угол CMA. Ответ дайте в градусах.

|
|
21. Катеты прямоугольного треугольника равны  и 1. Найдите синус наименьшего угла этого треугольника. и 1. Найдите синус наименьшего угла этого треугольника.

|
22. В прямоугольном треугольнике ABC катет AC = 75, а высота CH, опущенная на гипотенузу, равна   Найдите Найдите 

|
|
23. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если угол DEC равен 53°. Ответ дайте в градусах.
|
24. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.

|
|
25. Диагональ AC параллелограммаABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.

|
26. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 71°, угол CAD равен 61°. Найдите угол ABC. Ответ дайте в градусах.
|
|
27. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
В ответе запишите величины углов в порядке возрастания через точку с запятой.
|
28. Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
|
|
29. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 24 и 25

|
30. В треугольнике  угол С равен 90°, угол С равен 90°,  . Найдите АВ. . Найдите АВ.

|
|
31. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 14°, угол CAD равен 30°. Найдите угол ABC. Ответ дайте в градусах.
|
32. В треугольнике ABC BM — медиана и BH – высота. Известно, что AC = 216, HC = 54 и уголACB равен 40°. Найдите угол AMB. Ответ дайте в градусах.

|
|
33. Задание 9 № 132779. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
|
34. Периметр равнобедренного треугольника равен 36, а основание равно 16. Найдите площадь треугольника.

|
- Диагональ BD параллелограмма ABCDобразует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограммА

|
36. Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведенную к гипотенузе.
|
|
37.В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.

|
38. В треугольнике ABC угол C равен 90°, AC = 20, tgA = 0,5. Найдите BC.
|
|
.
39. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
|
40. В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 84 и BC = BM. Найдите AH.

|
|
41. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 80°, угол CAD равен 54°. Найдите угол ABD. Ответ дайте в градусах.
|
42. В треугольнике АВС АС = 35,  угол С равен 90°. Найдите радиус описанной окружности этого треугольника. угол С равен 90°. Найдите радиус описанной окружности этого треугольника.

|
|
43. Биссектрисы углов N и M треугольника MNP пересекаются в точке A. Найдите  , если , если  , а , а 

|
44. Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
|
|
45. Прямые m и n параллельны. Найдите угол3, если угол 1 равен 22°, угол 2 равен 72°. Ответ дайте в градусах.

|
46.. В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 64 и CH = 16. Найдите cosB.

|
|
47. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

|
48. В треугольнике ABC угол C прямой, BC = 3 , cosB = 0,6. Найдите AB.

|
|
49. Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите уголORQ. Ответ дайте в градусах.

|
50. В треугольнике OAB угол B равен 90°, AB = 6, sin О = 0,3. Найдите OA.

|





 .
.

 Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите
Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите  , если
, если  , а
, а 








 ,
,  ,
,  . Найдите
. Найдите  . Ответ дайте в градусах.
. Ответ дайте в градусах.
 катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
 Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.
Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.

 и 1. Найдите синус наименьшего угла этого треугольника.
и 1. Найдите синус наименьшего угла этого треугольника.

 Найдите
Найдите 




 угол С равен 90°,
угол С равен 90°,  . Найдите АВ.
. Найдите АВ.





 угол С равен 90°. Найдите радиус описанной окружности этого треугольника.
угол С равен 90°. Найдите радиус описанной окружности этого треугольника.
 , если
, если  , а
, а 







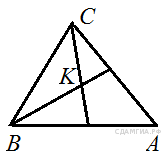 Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите
Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите