Линейная функция и её график

Задания по карточкам в 4 вариантах и таблица ответов

Карточка №1

Задана линейная функция у = 1/3х + 3

1. укажите коэффициент m.

2. Убывающая или возрастающая эта функция?

3. Найдите значение функции при х = 24.

4. Постройте график функции и укажите по графику, чему равно значение аргумента при у = 4.

5. Найдите по графику наибольшее значение на отрезке -3≤х≤6.

6. Найдите по графику наименьшее значение функции на полуинтервале -6≤х≤3.

7. Укажите ординату точки пересечения с осью абсцисс.

(должно получиться слово «алгебра»)

Карточка №2

Задана линейная функция: у = 0,5х – 2

1. Назовите коэффициент к

2. Найдите значение функции, если значение аргумента х = -2

3. Постройте график функции и найдите по графику значение аргумента при у = 4

4. Найдите ординату точки пересечения графика функции с осью ОУ

5. По графику найдите наибольшее или наименьшее значение функции

при х≥-4

По графику найдите наибольшее значение функции на отрезке -6≤х

Итоговое слово «Рекорд»

Карточка №3

Задана линейная функция у = -2х – 3

1. Выясните, возрастает или убывает заданная функция

2. Назовите коэффициент m

3. Найдите значение функции, если значение аргумента х = 0,5

4. Постройте график функции и найдите по графику значение аргумента, если значение функции у = -5

5. Найдите абсциссу точки пересечения графика функции с осью ОХ

6. Найдите по графику наибольшее или наименьшее значение функции при -3≤х≤5

7. По графику найдите наибольшее значение функции на отрезке -4≤х≤3

Ключевое слово «Лейбниц»

Карточка №4

Дана линейная функция у = - х + 5

1. Чему равен коэффициент к?

2. Найдите значение функции, если значение аргумента х = 8

3. Постройте график функции и найдите по графику значение аргумента, соответствующее значению у, равному 15

4. По графику найдите ординату точки пересечения с осью ОУ

5. По графику найдите наименьшее значение функции на отрезке -3≤х≤9

6. По графику найдите наибольшее или наименьшее значение функции

при х≥-3

Ключевое слово «Декарт»

Таблица ответов

Тема урока: Линейная функция и ее график.

Урок-путешествие

Цели:

• образовательные: формировать знания учащихся по теме; учить строить и исследовать график линейной функции; учить мыслить самостоятельно и делать выводы;

• развивающие: развивать логическое мышление, память, внимание, умение сравнивать, обобщать;

• воспитательные: воспитывать математическую культуру, трудолюбие, взаимопомощь, умение контролировать свои действия.

Структура урока:

1. Организационный момент. Сообщение темы урока.

2. Устная работа

3. Актуализация опорных знаний.

4. Работа по теме урока.

5. Закрепление темы. Эстафета.

6. Работа по теме урока: по карточкам в парах (самоконтроль)

7. Историческая справка.

8. Подведение итогов учебной деятельности

Оборудование: интерактивный комплекс (проектор, экран); диск с презентацией: чертежные инструменты; карточки с буквами; раздаточный материал.

Ход урока

1. Организационный момент (2 мин.)

Подготовка к уроку.
Объявление темы урока и ее запись учащимися.

Учитель: Ребята, сегодня на уроке мы совершим с вами путешествие в новую страну.

Слайд 1, см. Приложение 1

2. Устная работа (5 мин.)

Сначала пройдем пассажирский досмотр на таможне. Слайд 2

Среди заданных укажите линейные уравнения:

1) 5y = x

2) 3y = 0

3) y ²+ 16x² = 0

4) 8/x + y = 4

5) 1/8 x + y =4

6) y = -x + 11

7) 7/y + 0.5x – 2 = 0

8) 25d – 2m + 1 = 0

9) y =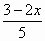 

3. Актуализация опорных знаний (4 мин.)

Учитель: А теперь мы вспомним то, что необходимо для нашей сегодняшней темы:

Слайд 3
а) Укажите коэффициенты в следующих линейных уравнениях:

1) 0,5x + y = 0
2) –x + 4 + 8y = 2
3) 11 + x – y = 0
4) 1/7y + 5 = x

Слайд 3
b) Выразите в этих уравнениях переменную у относительно переменной х. (На доске появляется решение задания. Все учащиеся проверяют):

1) y = -0,5x
2) y = 1/8 x – 0,25
3) y = x + 11
4) y = 7x – 35

4. Работа по теме урока. (8 мин.)

Слайды 4, 5

Что необходимо знать о линейной функции?

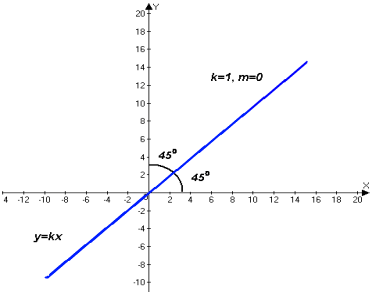
y = kx + m – линейная функция
х – аргумент (независимая переменная)
у – функция (зависимая переменная)
k, m – числа (коэффициенты)
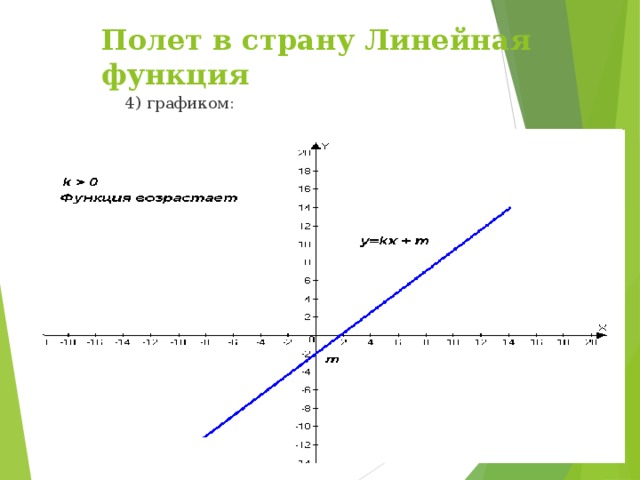
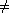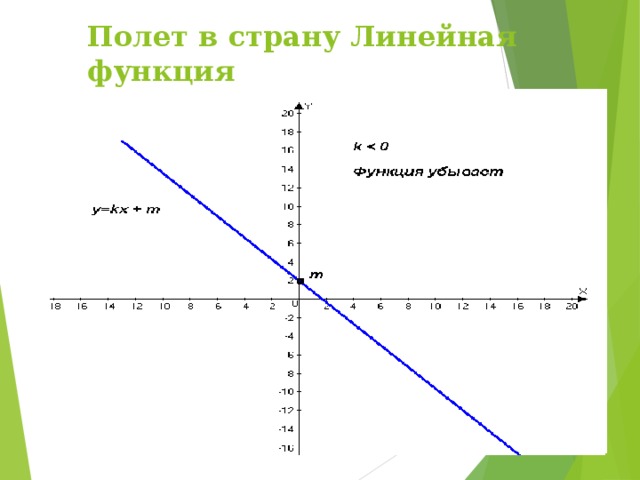
к  0

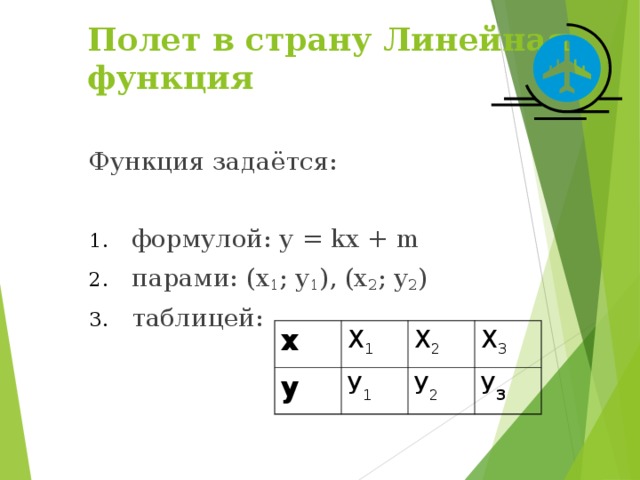
Функция задаётся:

1) формулой: у = kx + m

2) парами: (х₁; у₁), (х₂; у₂)

3) таблицей:

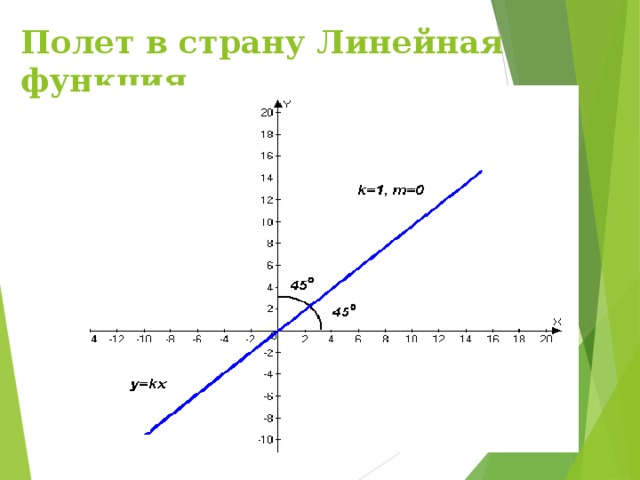
4) графиком:

Слайд 6

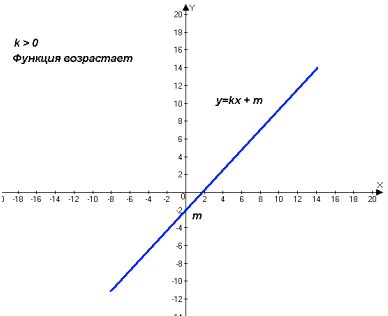
Слайд 7

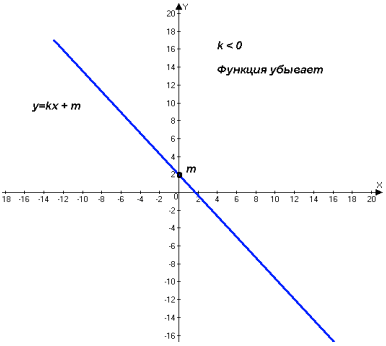
Слайд 8

Слайд 9

Совершим экскурсию по стране:

2х – у + 5 = 0 –линейное уравнение

Преобразуем в линейную функцию:

у = 2х +5
k = 2, m = 5

Учащимся в тетради подготовить пять рисунков координатной плоскости, за единичный отрезок принять 1 клетку тетради. Вдоль каждой оси не меньше девяти делений в положительном и отрицательном направлениях.

Выполнить задание 1:

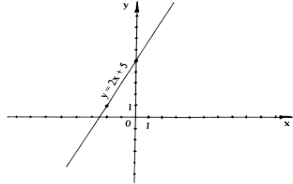
Слайд 10

а) Построить график функции у = 2х + 5

Слайд 11

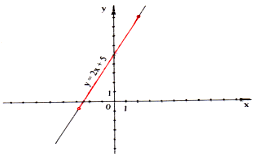
б) Построить график функции у = 2х + 5 при -3

Слайд 12

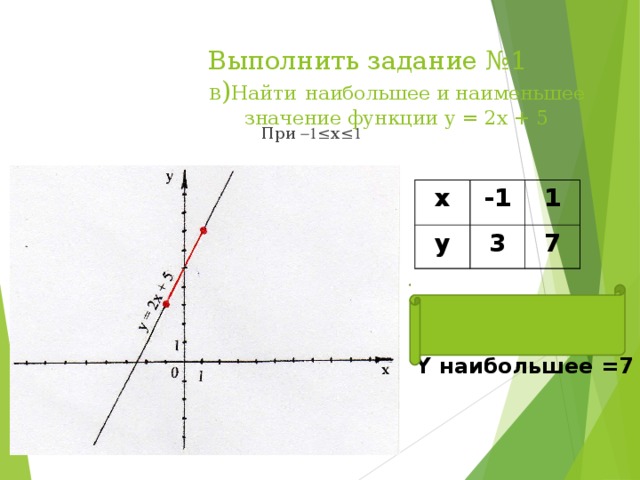
в) Найти наибольшее и наименьшее значение функции у = 2х + 5

а) при -1≤х≤ 1

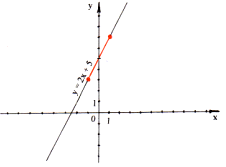
у наибольшее = 7
у наименьшее = 3

Слайд 13 
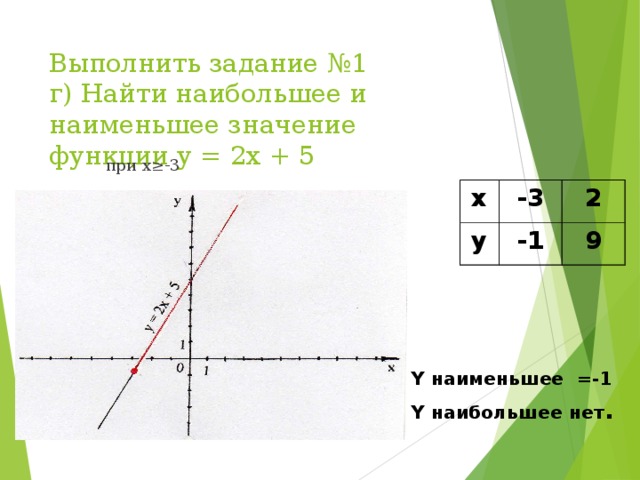
г) при х≥-3 

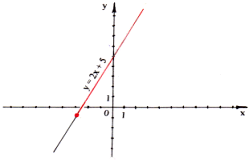
у наибольшее – нет
у наименьшее = -1

Слайд 14

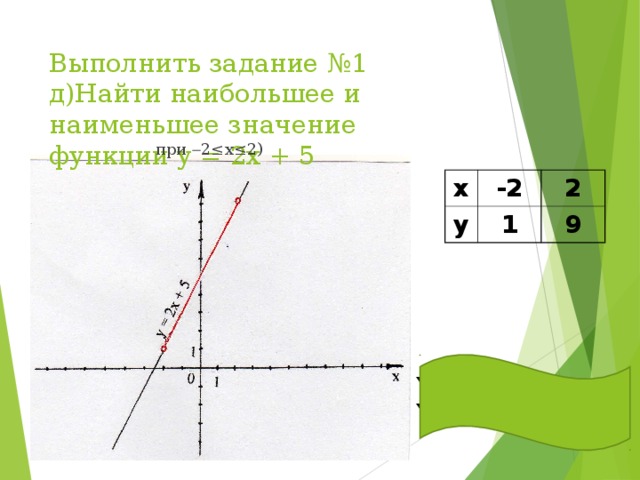
д) при -2

у наибольшее – нет
у наименьшее – нет

5. Закрепление темы. Эстафета (7 мин.)

По желанию ученики выходят к рабочей доске и выполняют задание№2 (всего 3 человека). По окончании выполнения задания каждый из них получает карточку с буквой и крепит ее на свободной части доски. Когда задание закончено, получается ключевое слово ПИЛОТЫ.

Задание 2:

Слайд 15

а) Построить график функции у = – х/2 + 3

1-й ученик делает таблицу и находит точки графика [ П] , строит график [И]

2-й ученик – указывает коэффициенты функции [Л], определяет является эта функция убывающей или возрастающей? Как определить это без графика? [О]

3-й ученик должен найти наибольшее и наименьшее значение функции:

1) при -4≤х≤2 [Т]; 
2) при -2≤х≤6 [Ы].

На Слайде 16 возникает слово пилоты.

Учитель: Наши пилоты проложили курс в загадочную страну Линейная функция

6. Работа по карточкам в парах (14 мин.)

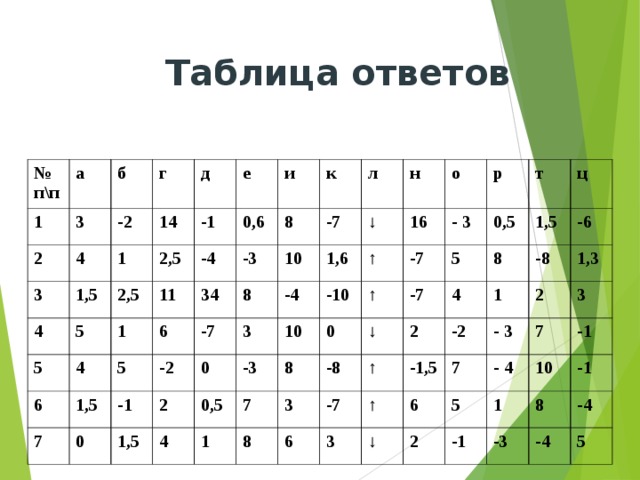
У каждой карточки есть ключевое слово, которое можно найти, выполнив задание и выбрав букву из таблицы на доске. Побеждают те пары, которые первыми выполнят один из четырех вариантов заданий карточки или больше других составят ключевых слов, решив несколько вариантов.

Ответы ученики сверяют на Слайде 18.

Задания по карточкам в 4 вариантах и таблица ответов в Приложении 2.

7. Историческая справка (2 мин.)

В результате самостоятельной работы по карточкам на доске появятся слова:

Карточка 1
алгебра – это слово произошло от названия сочинения Мухаммеда Аль-Хорезми “Аль-джебр и Аль-мукабала”, в котором алгебра излагалась как самостоятельный предмет. Слайд 19

Карточка 2
Роберт Рекорд – это английский математик, который в 1556г. ввёл знак равенства и объяснил свой выбор тем, что ничто не может быть более равным, чем два параллельных отрезка. Слайд 20

Карточка 3
Готфрид Лейбниц – немецкий математик (1646 – 1716г.г.), который первым ввёл термин “абсцисса” – в 1695г., “ордината” – в 1684г., “координаты” – в 1692г.Слайд 21

Карточка 4
Рене Декарт – французский философ и математик (1596 – 1650г.г.), который первым ввёл понятие “функция” Слайд 22

8. Подведение итогов (3 мин.)

Слайд 23

Обсуждение с учащимися, что нового они узнали. Оценить работу учащихся.
Дать домашнее задание.

Выводы.

Данная тема очень важна для изучения математики.

Тему “Функция” учащиеся начинают изучать с восприятия линейной функции. На данном этапе у школьников формируется очень важный стереотип мышления – через визуальное восприятие и практические навыки начинается исследовательская работа.

При использовании Презентации на уроке изучение материала начинается с определяющих компонент исследования функциональной зависимости алгебраического выражения. Основное внимание уделяется формированию у учащихся умения сопоставлять данные графика линейной функции с определенными условиями заданий. Происходит знакомство учащихся с новыми терминами (функция, коэффициент, линейная зависимость, возрастание и убывание графика функции)

Графики функций, продемонстрированные на слайдах Презентации, не только воспроизводят определенный объем информации темы в ее строго систематизированном виде, но вызывают у учащихся потребность прокомментировать и оценить изучаемое. Это делает слайды Презентации активным рабочим средством для закрепления и повторения. Так осуществляется обучающий этап урока.

Цель заданий при самостоятельной работе по карточкам – указать по таблице подходящие характеристики для выбранной функции. Эта работа направлена на формирование у учащихся умения проводить обоснования – важнейший этап закрепления изучаемого материала. По мере того, как учащиеся отвечают на соответствующие вопросы карточек и фиксируют ответы, у них появляется ключевое слово. Оно помогает узнать историю происхождения определенных терминов. Учащимся не требуется оформлять решение, что занимает время на уроке, нужно только применить теоретические знания для конкретного примера.

На этом уроке в игровой форме продемонстрированы все характерные особенности линейной функции так, что учащиеся свободно овладевают материалом по теме.

Урок – путешествие.

«Линейная функция

и её график»

учитель математики

Общеобразовательной школы №166

Федоркина Марина Владимировна

.

Таможенный досмотр Укажите линейные уравнения :

1) 6y = x

2) 5y = 0

3) 2y 2 + 32x 2 = 0

4) 8/x + y = 4

5) 1/8 x + y =4

6) y = -x + 11

7) 7/y + 0.5x – 2 = 0

8) 25d – 2m + 1 = 0

9) y = 3 – 2x

5

Посадка на самолет

Укажите коэффициенты в следующих линейных уравнениях:

1)0,5x + y = 0 2)–x + 4 + 8y = 2

3)11 + x – y = 0 4)1/7y + 5 = x

выразите в этих уравнениях переменную у относительно переменной х.

1) y = -0,5x

2) y = 1/8 x – 0,25

3) y = x + 11

4) y = 7x – 35

Полет в страну Линейная функция

y = kx + m – линейная функция

х – аргумент (независимая переменная)

у – функция (зависимая переменная)

k, m – числа (коэффициенты)

к ≠ 0

Полет в страну Линейная функция

Функция задаётся:

• формулой: у = kx + m
• парами: (х 1 ; у 1 ), (х 2 ; у 2 )
• таблицей:

х

Х 1

у

Х 2

У 1

Х 3

У 2

У 3

Полет в страну Линейная функция

4) графиком:

Полет в страну Линейная функция

Полет в страну Линейная функция

Экскурсия по стране

• 2х – у + 5 = 0 – линейное уравнение

Преобразуем в линейную функцию :

у = 2х +5

k = 2, m = 5

и построим график функции у = 2х + 5

Экскурсия по стране Выполнить задание №1

а)Построить график функции у = 2х + 5 :

х

у

0

-2

5

1

Экскурсия по стране

Выполнить задание №1 б)Построить график функции

у = 2х + 5 при -3≤х≤2

х

у

-3

2

-1

9

Выполнить задание №1 в ) Найти наибольшее и наименьшее значение функции у = 2х + 5

При  ≤х≤ 

х

-1

у

1

3

7

Y наименьшее =3

Y наибольшее =7

Выполнить задание №1 г) Найти наибольшее и наименьшее значение функции у = 2х + 5

при х≥-3

х

-3

у

2

-1

9

Y наименьшее =-1

Y наибольшее нет .

Выполнить задание №1 д)Найти наибольшее и наименьшее значение функции у = 2х + 5

при  2≤х≤2)

х

-2

у

2

1

9

Y наименьшее нет

Y наибольшее нет

№ 2 а) Построить график функции

у = -х/2 + 3

б) указать коэффициенты функции

в) указать является эта функция убывающей или возрастающей? Как определить это без графика?

г) найти наибольшее и наименьшее значение функции:

1. при -4≤х≤2

2. При -2≤х≤6

П И Л О Т Ы

Экскурсия по маршрутным листам

Таблица ответов

№

п\п

1

а

3

б

2

г

3

4

-2

1,5

14

1

4

д

5

2,5

5

е

2,5

-1

4

11

0,6

-4

и

6

1

34

-3

к

8

6

1,5

5

7

-7

8

-2

10

-1

-7

0

л

1,6

2

↓

-4

3

0

н

1,5

16

-3

-10

↑

о

10

0,5

4

7

8

- 3

р

0

-7

↑

1

0,5

-8

-7

8

3

↓

т

5

ц

2

1,5

-7

4

8

↑

6

1

-6

-1,5

↑

3

-8

-2

1,3

- 3

2

6

7

↓

3

- 4

2

5

7

1

10

-1

-1

-1

8

-3

-4

-4

5

Алгебра – это слово произошло от названия сочинения Мухаммеда Аль-Хорезми «Аль-джебр и Аль-мукабала», в котором алгебра излагалась как самостоятельный предмет

Роберт Рекорд – это английский математик, который в 1556г. ввёл знак равенства и объяснил свой выбор тем, что ничто не может быть более равным, чем два параллельных отрезка.

Готфрид Лейбниц – немецкий математик (1646 – 1716г.г.), который первым ввёл термин «абсцисса» - в 1695г., «ордината» - в 1684г., «координаты» - в 1692г.

Рене Декарт – французский философ и математик (1596 – 1650г.г.), который первым ввёл понятие «функция»

• Спасибо за внимание!