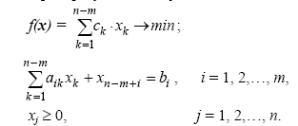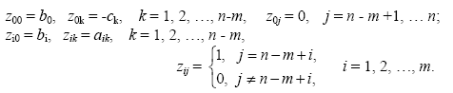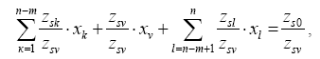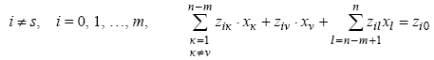«Дискретная математика»
Линейное программирование и симплекс метод.
Содержание
Стр.
Введение 3
1 Постановка задачи линейного программирования 5
2 Геометрическая интерпретация задачи линейного
программирования 6
3 Графическое решение двумерной задачи 9
4 Симплекс - метод при заданном начальном допустимом базис 10
5 Табличный симплекс – метод 16
Заключение 25
Список использованной литературы 26
Введение
Каждый человек ежедневно, не всегда осознавая это, решает проблему: как получить наибольший эффект, обладая ограниченными средствами.
Наши средства и ресурсы всегда ограничены. Жизнь была бы менее интересной , если бы это было не так. Не трудно выиграть сражение, имея армию в 10 раз большую, чем у противника; Ганнибалу, чтобы разбить римлян при Каннах, командуя вдвое меньшей армией, нужно было действовать очень обдуманно.
Чтобы достичь наибольшего эффекта, имея ограниченные средства, надо составить план, или программу действий. Раньше план в таких случаях составлялся «на глазок» (теперь, впрочем, зачастую тоже). В середине XX века был создан специальный математический аппарат, помогающий это делать «по науке». Соответствующий раздел математики называется математическим программированием. Слово «программирование» здесь и в аналогичных терминах («линейное программирование, динамическое программирование» и т.п.) обязано отчасти историческому недоразумению, отчасти неточному переводу с английского. По-русски лучше было бы употребить слово «планирование». С программированием для ЭВМ математическое программирование имеет лишь то общее, что большинство возникающих на практике задач математического программирования слишком громоздки для ручного счета, решить их можно только с помощью ЭВМ, предварительно составив программу.
Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Леонида Витальевича Канторовича «Математические методы организации и планирования производства». Поскольку методы, изложенные Л.В.Канторовичем, были мало пригодны для ручного счета, а быстродействующих вычислительных машин в то время не существовало, работа Л.В.Канторовича осталась почти не замеченной.
Свое второе рождение линейное программирование получило в начале пятидесятых годов с появлением ЭВМ. Тогда началось всеобщее увлечение линейным программированием, вызвавшее в свою очередь развитие других разделов математического программирования. В 1975 году академик Л.В.Канторович и американец профессор Т.Купманс получили Нобелевскую премию по экономическим наукам за «вклад в разработку теории и оптимального использования ресурсов в экономике».
Эти премии получили свое название в честь их учредителя – известного химика и изобретателя Альфреда Нобеля, они должны были присуждаться за научные открытия в области физики, химии, физиологии или медицины, за литературные произведения, «отражающие человеческие идеалы», а так же тем, кто «внесет весомый вклад в сплочение народов, уничтожение рабства, снижение численности существующих армий и содействие мирной договоренности». Математикам премия не предназначалась. Однако в 1969 году Шведский банк по случаю 300-летия со дня своего образования учредил премию памяти А.Нобеля – по экономическим наукам. Она то и была присуждена в 1975 году Л.В.Канторовичу и Т.Купмансу за создание новой математической науки (получившей название линейного программирования) и применение этой теории в экономике.
В автобиографии, представленной в Нобелевский комитет, Леонид Витальевич Канторович рассказывает о событиях, случившихся в 1939 году. К нему, 26-летнему профессору-математику, обратились за консультацией сотрудники лаборатории планерного треста, которым нужно было решить задачу о наиболее выгодном распределении материала между станками. Эта задача сводилась к нахождению максимума линейной функции, заданной на многограннике. Максимум такой функции достигался в вершине, однако число вершин в этой задаче достигало миллиарда… Поэтому простой перебор вершин не годился. Леонид Витальевич писал: «оказалось, что эта задача не является случайной. Я обнаружил большое число разнообразных по содержанию задач, имеющих аналогичный математический характер: наилучшее использование посевных площадей, выбор загрузки оборудования, рациональный раскрой материала, распределение транспортных грузопотоков… Это настойчиво побудило меня к поиску эффективного метода их решения». И уже летом 1939 года была сдана в набор книга Л.В.Канторовича «Математические методы организации и планирования производства», в которой закладывались основания того, что ныне называется математической экономикой.
Американский математик А.Данциг в 1947 году разработал весьма эффективный конкретный метод численного решения задач линейного программирования (он получил название симплекс метода). Идеи линейного программирования в течении пяти шести лет получили грандиозное распространение в мире, и имена Купманса и Данцига стали повсюду широко известны.
1 Постановка задачи линейного программирования
Задача линейного программирования может рассматриваться как частный случай рассмотренной выше задачи минимизации скалярной функции векторного аргумента с ограничениями типа неравенств. Имеет широкое применение при решении экономических задач, задач, связанных с планированием производства, в теории надёжности, математической статистике и т.д.
В канонической форме задача линейного программирования представляется в виде:
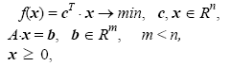
где f(х) - минимизируемая целевая функция, представляющая собой скалярное произведение заданного вектора c и искомого вектора х. Соотношение определяют область Х Є Rn допустимых значений вектора x или область определения целевой функции f(x). А - заданная матрица размером m×n, ранг которой равен m, b ≥ 0 - заданный вектор.
В скалярной форме соотношения представляются в виде:


Приведение задач линейного программирования к канонической форме
К канонической форме может быть приведён достаточный круг задач.
1. Задача максимизации целевой функции у = f(x) → max эквивалентна задаче минимизации её с противоположным знаком z = -f(x) → min.
2. Пусть i-е соотношение в представлено в виде неравенства
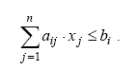
Введением дополнительной неотрицательной переменной хn+i ≥ 0 это неравенство всегда может быть представлено в виде равенства
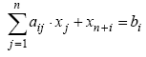
Аналогично, неравенство вида

введением дополнительной неотрицательной переменной хn+i ≥ 0 представляется в виде равенства
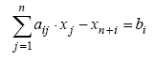
3. Путь переменная хj может принимать как положительные так и отрицательные значения. Введением двух неотрицательных переменных uj ≥ 0, vj ≥ 0 она представляется в виде разности
xj = uj - vj,
а задача линейного программирования будет содержать только неотрицательные переменные.
4. В тех случаях, когда условие не отрицательности переменных имеет более общий вид: xj ≥ bj, где bj - заданная постоянная, переходом к вспомогательной переменной уj ≥ 0 в результате преобразования
xj = уj + bj
задача линейного программирования приводится к канонической форме.
2 Геометрическая интерпретация задачи линейного программирования
Рассмотрим частную задачу линейного программирования по минимизации функции двух переменных (n = 2)
f(х1, х2) = с1 ⋅ х1 + с2 ⋅ х2 → min

при наличии ограничений в виде неравенств двух типов:
аi1 ⋅ х1 + аi2 ⋅х2 ≤ bi, i = 1, 2 …, m,
х1 ≥ 0, х2 ≥ 0,
определяющих область  допустимых значений вектора х*. Действительно, каждому неравенству (6.12) соответствует допустимая полуплоскость на плоскости х10х2 (см. рис), границей которой является прямая
допустимых значений вектора х*. Действительно, каждому неравенству (6.12) соответствует допустимая полуплоскость на плоскости х10х2 (см. рис), границей которой является прямая
аi1 ⋅ х1 + аi2 ⋅х2 = bi , i = 1, 2 …, m,
все точки которой принадлежат допустимой полуплоскости (штриховка со стороны недопустимой области). Поскольку все указанные полуплоскости являются выпуклыми множествами, то их пересечение образует выпуклое множество Χ допустимых значений вектора x. Если это множество не пусто, то оно представляет собой в общем случае выпуклый многогранник, а для рассматриваемого случая - выпуклый многоугольник.
Решение задачи линейного программирования (если оно существует) обязательно принадлежит одной из вершин указанного многогранника Χ. Действительно, в рассматриваемом частном случае линия постоянного уровня целевой функции представляет собой прямую с1х1 + с2х2 = С, С = const, на плоскости х10х2. Будем перемещать её в направлении анградиента -р(х) = (-с1, -с2)Т (в направлении уменьшения целевой функции) до тех пор, пока хотя бы одна точка этой прямой принадлежит области Χ. Поскольку сторонами многоугольника Χ являются отрезки прямых, то граничной в рассматриваемом случае является точка пересечения их.
Итак, в невырожденных случаях решение задачи единственно и обязательно совпадает с одной из вершин многогранника Χ, т.е. в этой точке х*Є Χ целевая функция f(х) имеет на множестве Χ Є Rn наименьшее значение
f(х*) = minf(х),
х Є Χ.
Вырожденные случаи задачи линейного программирования:
1. Множество Χ пусто.
2. Множество Χ таково  , что одна из его сторон параллельна линии постоянного уровня f(х) = const. Функция f(х) принимает своё наименьшее значение во всех точках отрезка АВ, т.е. задача имеет бесчисленное множество решений.
, что одна из его сторон параллельна линии постоянного уровня f(х) = const. Функция f(х) принимает своё наименьшее значение во всех точках отрезка АВ, т.е. задача имеет бесчисленное множество решений.
3. Множество Χ незамкнуто  . Линия постоянного уровня в направлении анградиента может перемещаться до бесконечности. Конечного решения задача не имеет. Сам факт не замкнутости множества Χ не означает, что задача не может иметь единственного решения. Например, задача максимизации функции f(х) при тех же условиях имеет решение в точке0.
. Линия постоянного уровня в направлении анградиента может перемещаться до бесконечности. Конечного решения задача не имеет. Сам факт не замкнутости множества Χ не означает, что задача не может иметь единственного решения. Например, задача максимизации функции f(х) при тех же условиях имеет решение в точке0.
3 Графическое решение двумерной задачи
Рассматриваемая задача минимизации линейной функции двух переменных при наличии линейных ограничений типа неравенств позволяет получить наглядное графическое решение, иллюстрирующее приведённые выше положения.
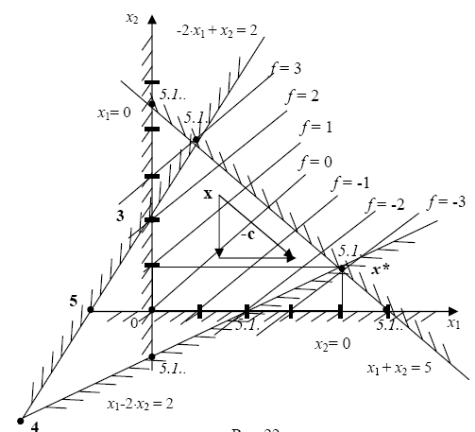
Пример 9
Минимизировать функцию
f(х) = -х1 + х2 → min
при наличии ограничений типа неравенств:
-2х1 + х2 ≤ 2,
х1 -2х2 ≤ 2,
х1 + х2 ≤ 5,
х1 ≥ 0, х2 ≥ 0.
Решение задачи:
1. Построение допустимой области Χ.
Каждое из неравенств заменяется равенством, в соответствии с которым в масштабе на плоскости х10х2 изображается прямая, являющаяся границей допустимой полуплоскости. Штриховка - со стороны недопустимой полуплоскости. Пересечение допустимых полуплоскостей образует искомый многоугольник 0АВСD (не заштрихованная область).
2. Отыскание оптимальной вершины. На рисунке для наглядности нанесены линии постоянного уровня целевой функции f(х) = С для ряда значений С, доказывающие, что наименьшее на множестве Χ значение целевой функции соответствует точке х* = (4, 1)Т и равно f(х*) = -3. В общем случае изображать на плоскости линии постоянного уровня нет необходимости. Достаточно в любой точке х координатной плоскости х10х2 построить вектор анградиента -р (х) = (-с1, -с2)Т = (+1, -1)Т. Линия постоянного уровня, проведённая через точку х, перпендикулярна ему. Перемещением этой линии параллельно самой себе в направлении вектора c определяется граничная вершина (точка В) и, следовательно, решение задачи.
4 Симплекс - метод при заданном начальном допустимом базисе
Как уже отмечалось, решение задачи линейного программирования, если оно существует, следует искать в одной из вершин допустимого многогранника Χ. Если размерность задачи невелика, то может быть использован метод перебора вершин с тем, чтобы выбрать ту из них, в которой целевая функция имеет наименьшее значение. Однако с увеличением размерности задачи метод перебора становится неэффективным даже с использованием ЭВМ.
Симплекс - метод - это метод целенаправленного перехода от одной вершины к другой по заданному алгоритму, разработанному с учётом его реализации на ЭВМ. Метод заключается в следующем:
1. Каким-либо образом определяется начальная допустимая вершина.
2. Формируется итерационный процесс, на каждом шаге которого осуществляется переход от одной вершины многогранника Χ к одной из соседних допустимых вершин. Из соседних вершин выбирается вершина, в которой ожидается наибольшее уменьшение целевой функции.
3. Если при переходе из некоторой вершины в любую соседнюю допустимую вершину значение целевой функции увеличивается, значит, целевая функция в этой вершине достигает своего наименьшего значения. Это и есть решение поставленной задачи.
4. Доказывается, что если задача не вырождена, то итерационный процесс заканчивается за конечное число шагов (поскольку число вершин конечно).
Приведём к канонической форме частную задачу, рассмотренную в разделе 2. Для этого в соответствии с вводятся дополнительные неотрицательные переменные х2+i ≥ 0, i = 1, 2, …, m, по одной в каждое из неравенств, превращая их в равенства, а вся задача представляется в виде:
f(х1, х2) = с1 ⋅ х1 + с1 ⋅ х1 → min,
аi1 ⋅ х1 + аi2 ⋅ х2 + х2+i = bi, i = 1, 2, …, m,
хj ≥ 0, j = 1, 2, …, m +2
Равенства в образуют систему из m линейных алгебраических уравнений с m +2 переменными. Если ранг матрицы А, образованной из коэффициентов аij, равен m, то, задав каким-либо образом значения любых двух переменных, оставшиеся m переменные однозначно определяются решением уравнений. Эти m переменные называются базисными, а две первоначально заданные переменные - свободными. Для упрощения решения задачи свободные переменные всегда выбирают равными нулю!
На каждой прямой, образующей границу области Χ, одна из переменных равна нулю. В заштрихованной полуплоскости эта переменная отрицательна, в незаштрихованной - положительна. Как уже отмечалось, пересечение двух границ в рассматриваемой частной задаче образует вершину многоугольника. Следовательно, в вершинах две переменные (свободные) равны нулю, остальные (базисные) определяются решением уравнения А x = b и могут быть как положительными, так и отрицательными (и даже равными нулю). Этот набор свободных и базисных переменных называется базисом или базисной точкой.
Если все базисные переменные неотрицательны, то базис называется допустимым. Если хотя бы одна из базисных переменных отрицательна, то базис - недопустимый (точки Е, М, N, F, K на рисунке). Все допустимые базисные точки являются вершинами многоугольника X.
В рассматриваемой частной задаче в качестве начального базиса удобно выбирать точку 0. В ней х1 = х2 = 0 (свободные переменные), а остальные - базисные переменные. Согласно равенствам из последние равны свободным коэффициентам bi правых частей уравнений, х2+i = bi. Но равенства всегда записываются так, чтобы bi ≥ 0, i = 1, 2, …, m. Следовательно, рассматриваемый базис допустимый.
Перейти из одной базисной точки в какую-либо соседнюю базисную точку означает, что одну из свободных переменных нужно перевести в разряд базисных переменных, а одну из базисных - сделать свободной. При этом должны быть выполнены два условия:
1) новый базис должен быть допустимым;
2) значение целевой функции в новом базисе не должно увеличиться.
Пример 9 (продолжение)
Дальнейшее уточнение алгоритма решения задачи линейного программирования удобно продемонстрировать на рассмотренной ранее задаче, заданной соотношениями.
В канонической форме она имеет вид:
f(x) = -х1 + х2 → min;
-2х1 + х2 + х3 = 2;
х1 - 2х2 + х4 = 2;
х1 + х2 + х5 = 5,
хj ≥ 0, j = 1, 2, …, 5,
где х3, х4, х5 - неотрицательные дополнительные переменные.
Начальный допустимый базис (точка О на рисунке):
Свободные переменные Базисные переменные
х1, х2 х3, х4, х5
х1 = 0, х2 = 0. Базисные переменные определяются равенствами и равны свободным коэффициентам: х3 = 2, х4 = 2, х5 = 5.
Первый шаг итерационного процесса
Проблема перехода от заданной базисной точки к новой базисной точке решается в два этапа.
I. На первом этапе отвечают на вопрос:
Какую из свободных переменных следует перевести в разряд базисных ?
При переводе любой свободной переменной в разряд базисных её значение увеличивается от нуля до некоторой положительной величины. Значение целевой функции при этом должно уменьшиться. Анализ выражения (6.18) показывает, что при увеличении х1 (х2 остаётся равной нулю) значение функции f(х) уменьшается, а при увеличении х2 (х1 = 0) - увеличивается. Обусловлено это тем, что в выражении коэффициент при х1 (с1 = -1) отрицательный, а при х2 (с2 = 1) - положительный. Если бы оба коэффициента с1 и с2 были отрицательными, то следовало бы выбрать переменную с наибольшим по модулю коэффициентом. Если бы оба эти коэффициента с1 и с2 были положительными, то данный базис следовало бы признать оптимальным, т.к. при переходе в любую соседнюю вершину значение целевой функции обязательно увеличилось бы.
Итак, в рассматриваемом случае свободную переменную х1 следует перевести в разряд базисных. Это действие удобно обозначить так: х1→.
I. На втором этапе решается вопрос:
Какую из базисных переменных следует перевести в разряд свободных?
Для решения этого вопроса удобно базисные переменные выразить через свободные, т.е. преобразовать уравнения к виду:
х3 = 2 + 2х1 - х2,
х4 = 2 - х1 +2х2,
х5 = 5 - х1 - х2.
При переводе любой базисной переменной в разряд свободных она от некоторой положительной величины уменьшается до нуля. В уравнениях (6.20) х2 = 0. При увеличении значения х1 переменная х3 увеличивается и, следовательно, свободной быть не сможет. Переменные х4 и х5 при увеличении х1 уменьшаются и могут стать свободными, уменьшившись до нуля. В том случае, когда переменная х4 станет свободной (т.е. х4 = 0), х1 примет значение, равное 2 (х1 = 2). Когда х5 станет свободной (х5 = 0) - х1 = 5. В этих условиях в разряд свободных следует перевести ту из переменных х4 или х5, которая обеспечивает наименьшее значение х1, т.е. переменную х4 (если в свободные перевести х5, то при х1 =5 базисная переменная х4 примет отрицательное значение, х4 = -3, и новый базис будет недопустимым).
Учитывая все сказанное, базисную переменную х4 следует перевести в разряд свободных, что символически обозначается так: ←х4
III. Преобразования
Итак, на рассматриваемом шаге итерационного процесса переменные х1 и х4 меняются местами х1 →← х4 и образуется новый базис
| Свободные переменные | Базисные переменные |
| х4, х2 | х3, х1, х5 |
Далее следует целевую функцию f(х) и новые базисные переменные х3, х1, х5 выразить через новые свободные переменные х4, х2. Для этого выделяется уравнение, содержащее преобразуемые переменные х1 и х4, и определяется зависимость х1 от х2 и х4. После подстановки её :
f(х) = -2 - x2 + x4
x3 = 6 + 3 ⋅ x2 -2x4;
x1 = 2 + 2x2 - x4;
x5 = 3 - 3x2 + x4.
Таким образом, в новом базисе
f(x) = -2, x1 = 2, х2 = 0, x3 = 6, х4 = 0, x5 = 3.
Второй шаг итерационного процесса
I. Какую из свободных переменных х4 или х2 следует перевести в разряд базисных?
Анализ целевой функции в соотношениях (6.21) показывает, что только увеличение х2 может привести к уменьшению функции f(х). Следовательно, х2 нужно перевести в разряд базисных переменных х2 →.
II. Какую из базисных переменных х3, х1 или х5 следует перевести в разряд свободных?
Поскольку коэффициенты при х2 в первом и втором уравнениях (6.21) положительны, то переменные х3 и х1 невозможно перевести в разряд свободных, т.к. они увеличиваются при увеличении значения х2. Переменная х5 при этом уменьшается. Следовательно, базисная переменная х5 переводится в разряд свободных ← х5
III. Преобразование х2 →← х 5
Новый базис:
| Свободные переменные | Базисные переменные |
| х4, х5 | х3, х1, х2 |
Целевая функция f(х) и новые базисные переменные х3, х1, х2 выражаются через новые свободные переменные х4, х5:
f(х) = -3 + 32⋅ х4 + 31х5,
х3 = 9 - х4 - х5,
х1 = 4 - 31х4 + 32х5,
х2 = 1 + 31х4 - 31х5.
Таким образом, в новом базисе
f(х) = −3, х1 = 4, х2 = 1, х3 = 9, х4 = 0, х5 = 0.
Третий шаг итерационного процесса
I. Какую из свободных переменных х4 или х5 перевести в разряд базисных?
При переводе в разряд базисных свободные переменные увеличиваются. Поскольку коэффициенты при х4 и х5 в выражении для целевой функции положительны, то при переводе в базисные как х4, так и х5, целевая функция увеличивается. Следовательно, рассматриваемый базис оптимален. Решение задачи: х1* = 4, х2* = 1, f(х*) = -3.
5 Табличный симплекс – метод
Итерационный процесс решения задачи линейного программирования удобно проиллюстрировать с помощью симплекс-таблиц. В этом разделе будет рассматриваться задача с заданным начальным допустимым базисом. В следующем разделе приведён один из методов нахождения начального допустимого базиса при общей постановке задачи.
Для того чтобы можно было считать, что начальный допустимый базис задан, необходимо выполнить три условия:
1. Из общего числа n переменных какие-либо n-m переменные признать свободными, а m переменные - базисными.
2. Целевая функция f(х) должна быть выражена только через свободные переменные.
3. Базисным переменным в матрице А уравнения bx=A должны соответствовать единичные столбцы, т.е. в каждом из скалярных уравнений

может быть только по одной базисной переменной с коэффициентом аij, равным единице, остальные коэффициенты при базисных переменных равны нулю. В этих условиях базисные переменные равны свободным коэффициентам bi и по определению неотрицательны. Рассматриваемый базис является допустимым.
Не нарушая общности задачи, будем считать, что первые n-m переменные являются свободными, остальные – базисными
| Свободные переменные | Базисные переменные |
| Хk, k= 1, 2, …,n - m | хj, j = n-m + 1,…,n |
Рассматриваемая задача преобразуется к виду
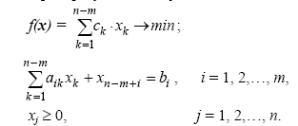
Удобно, чтобы выражение имело формально такой же вид, как и каждое из уравнений. Для этого вводится дополнительная переменная х0 = f(x) и соотношение записывается в виде уравнения

b0 - значение целевой функции (в рассматриваемых условиях b0 = 0).
Для ввода в ЭВМ формируется матрица коэффициентов {zij,} размером (m + 1)×(n + 1), i = 0, 1, …, m, j = 0, 1, …, n.
При этом
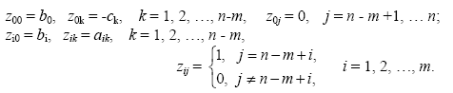
Все данные заносятся в таблицу коэффициентов первого шага итерационного процесса

Итак, нулевая строка таблицы содержит коэффициенты уравнения. z00 - значение целевой функции на каждом шаге итерационного процесса. На первом его шаге в первых n-m столбцах таблицы находятся коэффициенты при свободных переменных, в последних m столбцах - при базисных переменных (единичные столбцы). На последующих шагах свободные базисные переменные будут меняться, но список переменных в строке подписей остаётся неизменным, следовательно, единичные столбцы, соответствующие базисным переменным, будут перемещаться. В столбце подписей - обозначение целевой функции и набор базисных переменных, соответствующий данному шагу итерационного процесса. Около каждого из них в нулевом столбце таблицы находится их значение zi0, i = 0, 1, . . ., m.
В начале каждого шага итерационного процесса производится проверка, в ходе которой требуется ответить на два вопроса:
1. Уменьшилось ли значение целевой функции на этом шаге по сравнению с предыдущим?
Ответить на этот вопрос можно, начиная со второго шага, и для этого сравниваются значения z00 на двух соседних шагах итерационного процесса.
2. Является ли базис допустимым?
Для того чтобы базис был допустимым, все базисные переменные, а следовательно, коэффициенты zi0, i = 0, 1, . . ., m, нулевого столбца (кроме z00) должны быть неотрицательными.
На каждом шаге итерационного процесса рассматриваются три этапа решения задачи.
I этап. Производится анализ нулевой строки, т.е. zj0, j = 1, 2, . . ., n, при этом изучаются два вопроса:
а). Является ли данный базис оптимальным?
Базис оптимален, если перевод любой свободной переменной в базисную увеличивает целевую функцию х0 = f(х). Перевод свободной переменной в базисную означает её увеличение. Если все коэффициенты сk в выражении положительны, а, следовательно, коэффициенты z0k, k = 1,2…,n-m, при свободных переменных в отрицательны, то базис оптимален. Поскольку коэффициенты нулевой строки при базисных переменных равны нулю, то справедливо правило: базис оптимален, если все z0j, j = 1,2,…,n не положительны, z0j ≤ 0 (все коэффициенты нулевой строки, кроме z00, не положительны).
б). Если хотя бы один из коэффициентов z0j, j = 1,2, …, n положительный, то базис неоптимальный и решается вопрос: Какую из свободных переменных следует перевести в базисную?
Очевидно, что в базисные следует перевести ту свободную переменную хv, которая приведёт к наибольшему уменьшению целевой функции в новом базисе. Этой переменной в нулевой строке должен соответствовать наибольший положительный коэффициент z0v
z0v = max z0j, j = 1, …, n.
Таким образом, свободная переменная хv переводится в разряд базисных переменных хv→ .
II этап. В матрице Z и в табл. 1 выделяется v-й столбец - ведущий столбец. В результате анализа элементов ziv, i = 1, 2, …, m, этого столбца следует ответить на два вопроса:
а). Имеет ли рассматриваемая задача дальнейшее решение?
Чтобы задача имела дальнейшее решение, необходимо, чтобы хотя бы одну из базисных переменных можно было перевести в разряд свободных. Для этого её от некоторого положительного значения нужно уменьшить до нуля, т.е. должен быть положительным соответствующий этой переменной коэффициент ziv ведущего столбца. Если среди коэффициентов ziv , i = 1, 2, …, m, нет положительных, то ни одна из базисных переменных не может быть переведена в свободную, и задача не имеет решения.
б). Если хотя бы один из коэффициентов ziv положительный, то решается вопрос:
Какую из базисных переменных следует перевести в разряд свободных?
При переводе переменной хV из свободных в базисные те базисные переменные хi, которым соответствуют положительные коэффициенты ziv, будут уменьшаться. Из них выбирают переменную хs, которая первой уменьшается до нуля. Чтобы это осуществить для каждой базисной переменной хi с положительным коэффициентом ziv, вычисляется то значение хv, которое она приняла бы, если бы хi стала свободной, т.е. при хi = 0. Очевидно, что хv = ivizz0. Базисная переменная хs, которой соответствует наименьшее отношение svszz0 из отношений ivizz0, переводится в разряд свободных ← хs .

В матрице Z (и в табл. 1) выделяется ведущая строка коэффициентов zj , j = 0, 1, …, n. Коэффициент zsv, находящийся на пересечении ведущего столбца ziv, i = 0, 1, …, m, и ведущей строки zsj, j = 0, 1, …, n, называется ведущим элементом.
Итак, если базис не оптимален и задача имеет дальнейшее решение , то по окончании первых двух этапов осуществляется замена
xv →← х s,
т.е. свободная переменная хv переводится в разряд базисных, а базисная переменная хs - в разряд свободных.
III этап. Преобразование матрицы Z в матрицу Z′
Z′ - матрица коэффициентов на новом шаге итерационного процесса. Для вывода необходимых зависимостей в уравнения добавляются слагаемые с равными нулю коэффициентами, что приводит к общей форме записи этих уравнений:

Преобразования начинаются с ведущей строки

В новом базисе хV - базисная переменная, и следовательно, коэффициент при хV должен быть равен единице, а равенство должно быть записано в виде
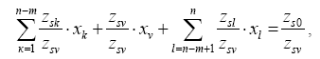
или в новых обозначениях уравнение имеет вид

Таким образом, имеем

В остальных строках матрицы при i ≠ s
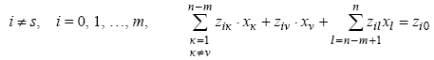
Подставляя выражения для хv, после некоторых преобразований получим

Для общности записи в уравнение искусственно введена переменная хv с нулевым коэффициентом. Тогда в новых обозначениях уравнение представляется в виде
,
Сравнивая коэффициенты при переменных в уравнениях, получим
Пример 9 (продолжение)
Ниже будет предложена демонстрация табличного симплекс-метода на ранее рассмотренном конкретном примере. Для этого соотношение преобразуем к виду
х0 + х1 - х2 = 0.
Тогда с учетом уравнений заполняется таблица первого шага итерационного процесса (табл. 2). Все коэффициенты записываются в верхнем левом углу каждой клетки таблицы.
1 шаг
Проверка
Все коэффициенты нулевого столбца, кроме нулевого коэффициента, положительны, следовательно, начальный базис допустимый.
I этап
а) среди коэффициентов нулевой строки (кроме нулевого) есть положительный, следовательно, базис не оптимальный;
б) наибольший коэффициент нулевой строки при х1. Эта переменная переводится из свободных в базисные х1→
Выделяется ведущий столбец.
II этап
а) среди коэффициентов ведущего столбца (кроме нулевого) есть положительные, следовательно, задача имеет дальнейшее решение;
б) для положительных коэффициентов ведущего столбца находится отношение свободного коэффициента к коэффициенту ведущего столбца . Эти соотношения записываются в соответствующую строку слева от таблицы. Выбирается наименьшее из них  , тогда базисная переменная х4 переводится в свободную ← х4. Выделяются ведущая строка и ведущий элемент zsv = 1.
, тогда базисная переменная х4 переводится в свободную ← х4. Выделяются ведущая строка и ведущий элемент zsv = 1.
Таблица 3
III этап
Преобразование матрицы Z в матрицу Z′ начинается с ведущей строки. Согласно выражению (6.30) для этого каждый старый коэффициент строки делится на ведущий элемент, и результат записывается в правом нижнем углу и как-либо выделяется. Выражение для расчета оставшихся коэффициентов матрицы Z′ достаточно сложно. Поэтому сначала вычисляются произведения  , которые записываются в нижнем правом углу, а вычитание в производится при оформлении следующей таблицы. В произведении
, которые записываются в нижнем правом углу, а вычитание в производится при оформлении следующей таблицы. В произведении  вторые сомножители, определенные выражением, уже вычислены. Это выделенные нижние элементы ведущей строки. Первые сомножители ziv - выделенные (старые) коэффициенты ведущего столбца.
вторые сомножители, определенные выражением, уже вычислены. Это выделенные нижние элементы ведущей строки. Первые сомножители ziv - выделенные (старые) коэффициенты ведущего столбца.
При формировании следующей таблицы строка подписей остаётся неизменной. В столбце подписей переменная х4 заменяется на х1. Новая таблица всегда начинается с заполнения выделенными коэффициентами ведущей строки предыдущей таблицы (s = 2), записываемыми в левом верхнем углу клеток новой таблицы. В остальные клетки в их левый верхний угол записываются результаты вычитания чисел, расположенных в разных углах соответствующей клетки табл. 2.
2 шаг
Проверка
а) в новом базисе f(x) = -2, что меньше f(x) = 0 старого базиса;
б) все элементы нулевого столбца (кроме нулевого) положительны. Новый базис допустимый.
I этап
а) среди коэффициентов нулевой строки (кроме нулевого) есть положительный (см. табл. 3). Базис не оптимален;
б) единственный положительный коэффициент нулевой строки при переменной х2. Она переводится из свободной в базисную х2→ .
II этап
а) в выделенном ведущем столбце (кроме нулевого) есть положительный коэффициент. Задача имеет дальнейшее решение;
б) единственному положительному коэффициенту ведущего столбца соответствует переменная х5. Она переводится из базисной в свободную ← х5 .
III этап
Производится преобразование матрицы Z в матрицу Z′ подобно тому, как это делалось на 1-м шаге. При заполнении новой таблицы в столбце подписей х5 заменяется на х2. В третьей строке табл. 4 записываются выделенные коэффициенты ведущей строки табл.3 Остальные элементы табл.4 получены в результате вычитания из верхнего столбца нижнего числа соответствующей клетки табл.3.
3 шаг
Проверка
а) значение целевой функции в новом базисе (f(х) = -3) меньше, чем в старом (f(х) = -2);
б) базисные переменные положительные.
I этап
а) среди коэффициентов нулевой строки (кроме нулевого) нет положительных. Базис оптимален. Решение задачи в нулевом столбце матрицы Z (и табл. 4) (значение целевой функции и базисных переменных)
f(х*) = -3, х3 = 9, х1 = 4, х2 = 1.
Переменные х4, х5 (не нулевые коэффициенты нулевой строки) - свободные, х4 = х5 = 0.
Заключение
Линейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать.
Таким образом, мы видим, что линейное программирование можно использовать не только для решения задач максимизации прибыли в предприятии, но и для решения задач минимизации всяческих убытков, которые могут понести социальные службы.
Проведение подобных исследований имеет не только высокое экономическое, но и социальное значение, если проанализировать эту сферу деятельности.
Список использованной литературы
1. Акулич И.Л. Математическое программирование в задачах и упражнениях. - М.: Высшая школа, 1993.
в управлении войсками».
2. Васильев Ф.П. Численные методы решения экстремальных задач. - М.: Наука, 1980.
3. Горелик В.А., Ушаков И.А. Исследование операций. - М.: Машиностроение, 1986.
4. Интрилигатор М. Математические методы оптимизации и экономическая теория. - М.: Прогресс, 1975.
5. Курицкий Б.К. Поиск оптимальных решений средствами Excel 7.0. - Спб.: BHV, 1997.
6. Малявко К.Ф. «Применение математических методов в военном деле».
7. Мину М. Математическое программирование. Теория и алгоритмы. - М.: Наука, 1990.
8. Павловский Ю.Н. Имитационные модели и системы. - М.: Фазиз, 2000.
9. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: Учебное пособие для университетов. - М.: Высшая школа, Книжный дом “Университет”, 1998.
10. Самусевич Г.А., «Оптимизация функции векторного аргумента» : конспект лекций, Екатеринбург, Издательство УЦМ УПИ, 2005.
11. Фомин Г. П. Методы и модели линейного программирования коммерческой деятельности: Учебное пособие для вузов/Г. П. Фомин. – М.: Финансы и статистика, 2000.
12. Шикин Е.В. Чхартишвили А.Г. Математические методы и модели в управ-лении: Учебник для ВУЗов. - М.: Дело, 2000.
9







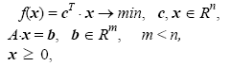

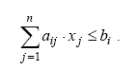
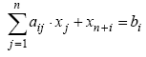

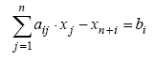

 , что одна из его сторон параллельна линии постоянного уровня f(х) = const. Функция f(х) принимает своё наименьшее значение во всех точках отрезка АВ, т.е. задача имеет бесчисленное множество решений.
, что одна из его сторон параллельна линии постоянного уровня f(х) = const. Функция f(х) принимает своё наименьшее значение во всех точках отрезка АВ, т.е. задача имеет бесчисленное множество решений.  . Линия постоянного уровня в направлении анградиента может перемещаться до бесконечности. Конечного решения задача не имеет. Сам факт не замкнутости множества Χ не означает, что задача не может иметь единственного решения. Например, задача максимизации функции f(х) при тех же условиях имеет решение в точке0.
. Линия постоянного уровня в направлении анградиента может перемещаться до бесконечности. Конечного решения задача не имеет. Сам факт не замкнутости множества Χ не означает, что задача не может иметь единственного решения. Например, задача максимизации функции f(х) при тех же условиях имеет решение в точке0.