Просмотр содержимого документа
«Тема: Решение симплекс-методом задачи линейного программирования.»
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»
( Н И У « Б е л Г У » )
ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА ПРИКЛАДНОЙ ИНФОРМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Исследование операций и методы оптимизации
Лабораторная работа №4
Тема: Решение симплекс-методом задачи линейного программирования.
студентки очного отделения
4 курса, 12001504 группы,
Марко С. Тангуила
Проверил:
Старший преподаватель
Болгова Евгения Витальевна
Белгород, 2018 год
Цель работы
Получение навыков самостоятельной алгоритмической и программной реализации на компьютерной технике симплекс-метода решения задачи линейного программирования в MatLab, научиться сводить оптимизационные задачи к задаче линейного программирования, заданную в допустимом каноническом виде.

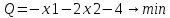
Результат выполнения работы
Матрица A коэффициентов системы имеет вид:
| 7 | 5 | 1 | 0 | 0 |
| -5 | 4 | 0 | 1 | 0 |
| 3 | -2 | 0 | 0 | 1 |
Первая часть системы ограничений уравнений имеет вид:
Составление симплексной таблицы. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка – это целевая функция. Последние три векторы-столбцы образуют базис в трехмерном пространстве. Следовательно, базисные переменные xB=[x3,x4,x5]T, а свободные переменные xF=[x1,x2]T:
| Базис | 1 | 2 | 3 | 4 | 5 |
|
| 3 | 7 | 5 | 1 | 0 | 0 | 35 |
| 4 | -5 | 4 | 0 | 1 | 0 | 20 |
| 5 | 3 | -2 | 0 | 0 | 1 | 2 |
|
| 1 | 2 | 0 | 0 | 0 | -4 |
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.
Выбор разрешающего столбца. Минимальный элемент pjj*=2.
Выбор разрешающей строки. Разрешающий столбец содержит положительные элементы a32=5 и a42=4. Найдем min(35:5, 20:4)=5 (минимум равен b4/a42). Следовательно, номер разрешающей строки i*=4. Разрешающий элемент a42=4, он выделен серым цветом.
Замена базиса:
в левом столбце новой таблицы на место 4 ставится 2. Остальные индексы остаются на своих местах.
на место элемента a42=4 в новой таблице пишем элемент a24=1:а42=1:4=1/4.Затем, вычисляются новые элементы вместо элементов разрешающего столбца и строки.
пересчитываются остальные элементы симплекс-таблицы по следующим формулам:
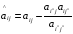 ,
,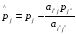 ,
, ,
,
| Базис | 1 | 2 | 3 | 4 | 5 |
|
| 3 | 53/4 | 0 | 1 | -5/4 | 0 | 10 |
| 2 | -5/4 | 1 | 0 | ¼ | 0 | 5 |
| 5 | ½ | 0 | 0 | ½ | 1 | 12 |
|
| 7/2 | 0 | 0 | -1/2 | 0 | -6 |
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.
В качестве разрешающего выберем столбец j*=1, так как это наибольший коэффициент. Разрешающий столбец содержит положительные элементы a31=53/4 и a51=1/2. Найдем min(10:53/4, 12:1/2)=40/53 (минимум равен b3/a31). Следовательно, номер разрешающей строки i*=3. Разрешающий элемент a31=53/4, он выделен серым цветом.
Пересчет симплекс-таблицы:
| Базис | 1 | 2 | 3 | 4 | 5 |
|
| 1 | 1 | 0 | 4/53 | -5/53 | 0 | 40/53 |
| 2 | 0 | 1 | 5/53 | 7/53 | 0 | 315/53 |
| 5 | 0 | 0 | -2/53 | 29/53 | 1 | 616/53 |
|
| 0 | 0 | -14/53 | -9/53 | 0 | 178/53 |
Среди коэффициентов целевой функции нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Оптимальный план можно записать так:
x1=40/53, x2=315/53, x3=0, x4=0, x5=616/53
F(X)=-1*40/53-2*315/53-4=-882/53≈16,6415
Код решения с помощью Matlab:
function lab4(x)
f=[-1 -2 0 0 0];
Aeq=[7 5 1 0 0; -5 4 0 1 0; 3 -2 0 0 1];
beq=[35 20 2];
lb=zeros(5,1);
[x,fval]=linprog(f,[],[],Aeq,beq,lb);
x
fval-4
Результат выполнения:









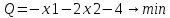
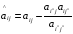 ,
,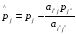 ,
, ,
,











