Тема урока: Линзы. Построение в линзах. Формула тонкой линзы.
Цель: дать знания о линзах, их физических свойствах и характеристиках.
Ход урока
I. Организационный момент
II. Изучение нового материала
Явление преломления света лежит в основе действия линз и многих оптических приборов, служащих для управления световыми пучками и получения оптических изображений.
Линза - это оптическое прозрачное тело, ограниченное сферическими поверхностями. Существует два вида линз:
а) выпуклые;
б) вогнутые.
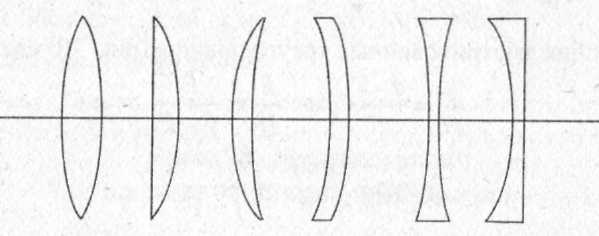
Выпуклые линзы бывают: двояковыпуклыми, плосковыпуклыми, вогнуто выпуклыми.
Выгнутые линзы могут быть: двояковогнутыми, плосковогнутыми, выпукло вогнутыми.
Линзы, у которых середины толще, чем края, называют собирающими, а у которых толще края - рассеивающими (слайды 3,4) .
Эксперимент
Пучок света направляют на двояковыпуклую линзу. Наблюдаем собирающее действие такой линзы: каждый луч, падающий на линзу, после преломления ею отклоняется от своего первоначального направления, приближаясь к главной оптической оси.
Описанный опыт естественным образом подводит учащихся к понятиям главного фокуса и фокусного расстояния линзы.
Расстояние от оптического центра линзы до ее главного фокуса называют фокусным расстоянием линзы. Обозначают ее буквой F, как и сам фокус (слайды 4-6).
Далее выясняется ход световых лучей через рассеивающую линзу. Аналогичным образом рассматривается вопрос о действии и параметрах рассеивающей линзы. Основываясь на экспериментальных данных, можно сделать вывод: фокус рассеивающей линзы мнимый (слайд 7).
III. Построение в линзах.
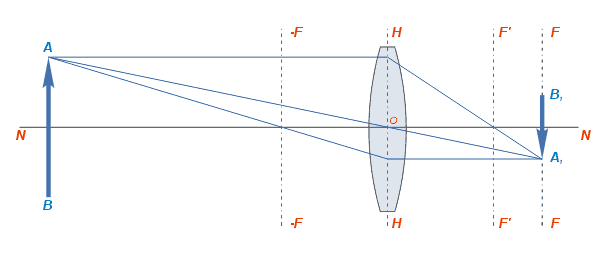
Построение линзой изображения предметов, имеющих определённую форму и размеры, получается следующим образом: допустим, линия AB представляет собой объект, находящийся на некотором расстоянии от линзы, значительно превышающем её фокусное расстояние.
От каждой точки предмета через линзу пройдёт бесчисленное количество лучей, из которых, для наглядности, на рисунке схематически изображен ход только трёх лучей.
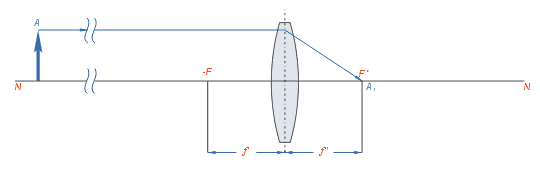
Если предмет находится на бесконечно далёком от линзы расстоянии, то его изображение получается в заднем фокусе линзы F’ действительным, перевёрнутым и уменьшенным до подобия точки.
Если предмет помещён между передним фокусом и двойным фокусным расстоянием, то изображение будет получено за двойным фокусным расстоянием и будет действительным, перевёрнутым и увеличенным.
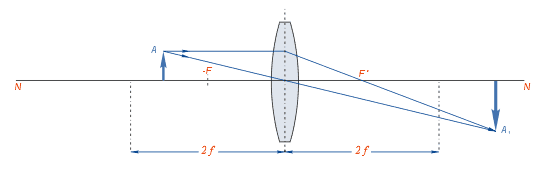
Если предмет помещён на двойном фокусном расстоянии от линзы, то полученное изображение находится по другую сторону линзы на двойном фокусном расстоянии от неё. Изображение получается действительным, перевёрнутым и равным по величине предмету.
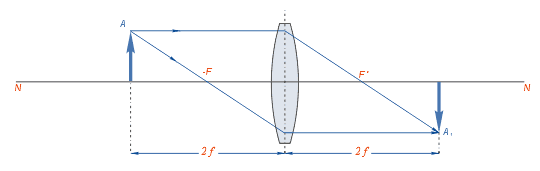

Если предмет приближён к линзе и находится на расстоянии, превышающем двойное фокусное расстояние линзы, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится за главным фокусом на отрезке между ним и двойным фокусным расстоянием.
Если предмет находится в плоскости переднего главного фокуса линзы, то лучи, пройдя через линзу, пойдут параллельно, и изображение может получиться лишь в бесконечности.
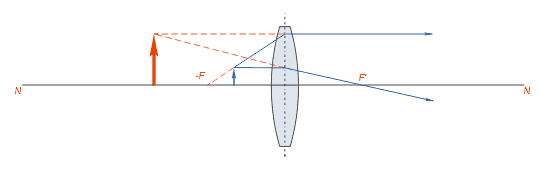
Если предмет поместить на расстоянии, меньшем главного фокусного расстояния, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимое, прямое и увеличенное, т. е. в данном случае линза работает как лупа5
)
IV. Вывод формулы тонкой линзы.
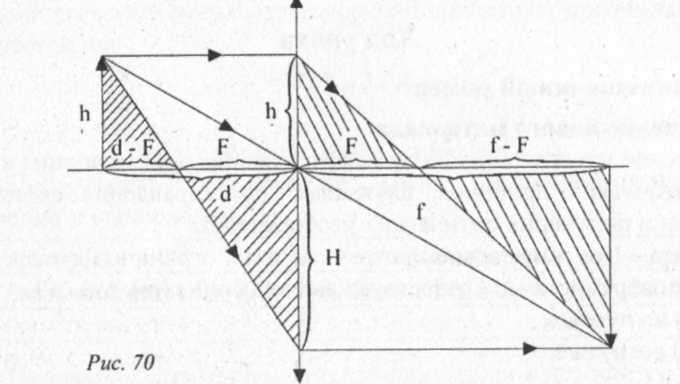
Из подобия заштрихованных треугольников (рис. 70) следует:
(слайд 17)
где d - расстояние предмета от линзы; f расстояние от линзы до изображения; F - фокусное расстояние. Оптическая сила линзы равна:
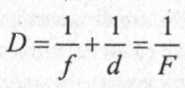
При расчетах числовые значения действительных величин всегда подставляются со знаком «плюс», а мнимых - со знаком «минус» (слайд 18).
Линейное увеличение
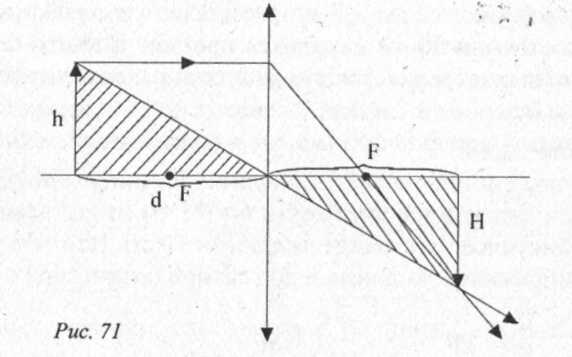
Из подобия заштрихованных треугольников (рис. 71) следует:
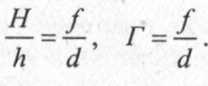 (слайд 19)
(слайд 19)
V. Закрепление изученного материала.
Почему фокус рассеивающей линзы называется мнимым?
Чем отличается действительное изображение точки от мнимого?
По какому признаку можно узнать: собирающая эта линза или рассеивающая, если судить только по форме?
Назовите свойство выпуклой линзы. (Собирать параллельные лучи в одну точку.)
Решение задач №№1064, 1066(Р) (слайды 20,21)
§ 63-65, №1065(Р)
2















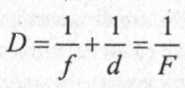

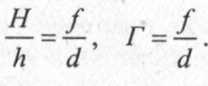 (слайд 19)
(слайд 19)









