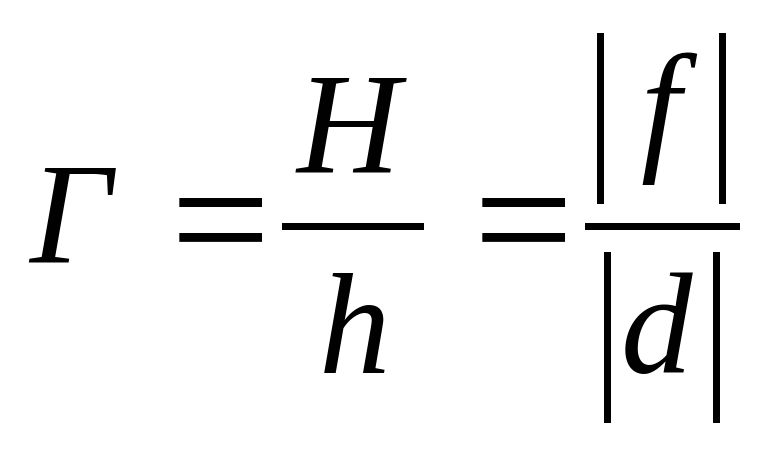м8 класс
«Линзы. Изображения, даваемые линзой. Формула тонкой линзы».
Цели урока:
Образовательные: сформировать понятия: линза, оптический центр, оптическая ось, фокус и фокусное расстояние, фокальная плоскость; обеспечить усвоение формул тонкой линзы и оптической силы; выработать умения строить изображения, даваемые линзами;
Воспитательные: продолжить формирование таких качеств, как аккуратность, точность, внимательность для получения правильных результатов и выводов при построении графическим методом изображений, даваемых линзами;
Развивающие: формировать умения применять полученные знания в изменённых и новых ситуациях.
Основной материал: Линзы, основные точки, линии. Собирающие и рассеивающие линзы. Оптическая сила линзы. Единица измерения – диоптрия. Построение изображений, даваемых линзами. Формула тонкой линзы. Линейное увеличение.
Организация деятельности учащихся.
1. Организационный момент. Мотивация учебной деятельности.
Ставится цель урока, намечаются пути её достижения и указываются критерии её достижения.
2. Формирование новых знаний (лекция)
Линзы, основные точки, линии. Собирающие и рассевающие линзы.
Определения:
- Линза (обычно изготавливаются из стекла);
- Тонкая линза – линза, толщина которой значительно меньше радиусов ограничивающих её сферические поверхности;
- Выпуклая, вогнутая линзы;
- Главная оптическая ось;
- Оптический центр линзы;
- Главный фокус;
- Фокальная плоскость;
- Фокусное расстояние;
- Рассеивающая, собирающая линзы;
- Побочная оптическая ось.
Прозрачные тела, ограниченные двумя сферическими поверхностями (хотя бы одной…), называются линзами.
|

Середина толще, чем края.
|

Середина тоньше, чем края.
|
|

|
Геометрические характеристики тонкой линзы:
- О – оптический центр линзы;
- MN – главная оптическая ось;
- F – главные фокусы линзы;
- Пл. F – фокальные плоскости;
- АВ – побочная оптическая ось (их множество).
|
Оптическая сила линзы, единица измерения.
Оптическая сила линзы.

1 дптр (диоптрий) →F=1 м
Построение изображений, даваемых линзами. Построить на доске и в теради.
|
Построение изображений в линзах.

1. Луч, || главной оптической оси после преломления проходит через фокус линзы.
2. Луч, проходящий через оптический центр не преломляется.
3. Луч, проходящий через фокус после прохождения через линзу становится || главной оптической оси.
|
d < F
|
увеличенное
|
прямое
|
мнимое
|
|
F < d < 2F
|
увеличенное
|
перевернутое
|
действительное
|
|
d > 2F
|
уменьшенное
|
перевернутое
|
действительное
|
|
d = 2F
|
натуральное
|
перевернутое
|
действительное
|
|
|
Построение изображения в рассеивающей линзе (изображение всегда мнимое).

|
|
Построение изображения точки лежащей на главной оптической оси.

Демонстрации. Преломление света в линзах. Используется прибор для изучения законов геометрической оптики.
Формула тонкой линзы.

d – расстояние от предмета до линзы,
f – расстояние от линзы до изображения.

 ;
;  ;
; 
Для рассеивающей линзы F и f нужно брать со знаком «минус»
Линейное увеличение.

Н – высота изображения,
h – высота предмета.
4. Самостоятельное построение учащимися для случаев
F < d < 2F, d = 2F, d > 2F
5.Домашнее задание. § 70-72, упр. 31 (3,4,5,6)8 класс
«Линзы. Изображения, даваемые линзой. Формула тонкой линзы».
Цели урока:
Образовательные: сформировать понятия: линза, оптический центр, оптическая ось, фокус и фокусное расстояние, фокальная плоскость; обеспечить усвоение формул тонкой линзы и оптической силы; выработать умения строить изображения, даваемые линзами;
Воспитательные: продолжить формирование таких качеств, как аккуратность, точность, внимательность для получения правильных результатов и выводов при построении графическим методом изображений, даваемых линзами;
Развивающие: формировать умения применять полученные знания в изменённых и новых ситуациях.
Основной материал: Линзы, основные точки, линии. Собирающие и рассеивающие линзы. Оптическая сила линзы. Единица измерения – диоптрия. Построение изображений, даваемых линзами. Формула тонкой линзы. Линейное увеличение.
Организация деятельности учащихся.
1. Организационный момент. Мотивация учебной деятельности.
Ставится цель урока, намечаются пути её достижения и указываются критерии её достижения.
2. Формирование новых знаний (лекция)
Линзы, основные точки, линии. Собирающие и рассевающие линзы.
Определения:
- Линза (обычно изготавливаются из стекла);
- Тонкая линза – линза, толщина которой значительно меньше радиусов ограничивающих её сферические поверхности;
- Выпуклая, вогнутая линзы;
- Главная оптическая ось;
- Оптический центр линзы;
- Главный фокус;
- Фокальная плоскость;
- Фокусное расстояние;
- Рассеивающая, собирающая линзы;
- Побочная оптическая ось.
Прозрачные тела, ограниченные двумя сферическими поверхностями (хотя бы одной…), называются линзами.
|

Середина толще, чем края.
|

Середина тоньше, чем края.
|
|

|
Геометрические характеристики тонкой линзы:
- О – оптический центр линзы;
- MN – главная оптическая ось;
- F – главные фокусы линзы;
- Пл. F – фокальные плоскости;
- АВ – побочная оптическая ось (их множество).
|
Оптическая сила линзы, единица измерения.
Оптическая сила линзы.

1 дптр (диоптрий) →F=1 м
Построение изображений, даваемых линзами. Построить на доске и в теради.
|
Построение изображений в линзах.

1. Луч, || главной оптической оси после преломления проходит через фокус линзы.
2. Луч, проходящий через оптический центр не преломляется.
3. Луч, проходящий через фокус после прохождения через линзу становится || главной оптической оси.
|
d < F
|
увеличенное
|
прямое
|
мнимое
|
|
F < d < 2F
|
увеличенное
|
перевернутое
|
действительное
|
|
d > 2F
|
уменьшенное
|
перевернутое
|
действительное
|
|
d = 2F
|
натуральное
|
перевернутое
|
действительное
|
|
|
Построение изображения в рассеивающей линзе (изображение всегда мнимое).

|
|
Построение изображения точки лежащей на главной оптической оси.

Демонстрации. Преломление света в линзах. Используется прибор для изучения законов геометрической оптики.
Формула тонкой линзы.

d – расстояние от предмета до линзы,
f – расстояние от линзы до изображения.

 ;
;  ;
; 
Для рассеивающей линзы F и f нужно брать со знаком «минус»
Линейное увеличение.

Н – высота изображения,
h – высота предмета.
4. Самостоятельное построение учащимися для случаев
F < d < 2F, d = 2F, d > 2F
5.Домашнее задание. § 70-72, упр. 31 (3,4,5,6)
Просмотр содержимого документа
«Линзы. Изображения, даваемые линзой. Формула тонкой линзы»
8 класс
«Линзы. Изображения, даваемые линзой. Формула тонкой линзы».
Цели урока: Образовательные: сформировать понятия: линза, оптический центр, оптическая ось, фокус и фокусное расстояние, фокальная плоскость; обеспечить усвоение формул тонкой линзы и оптической силы; выработать умения строить изображения, даваемые линзами;
Воспитательные: продолжить формирование таких качеств, как аккуратность, точность, внимательность для получения правильных результатов и выводов при построении графическим методом изображений, даваемых линзами;
Развивающие: формировать умения применять полученные знания в изменённых и новых ситуациях.
Основной материал: Линзы, основные точки, линии. Собирающие и рассеивающие линзы. Оптическая сила линзы. Единица измерения – диоптрия. Построение изображений, даваемых линзами. Формула тонкой линзы. Линейное увеличение.
Организация деятельности учащихся.
1. Организационный момент. Мотивация учебной деятельности.
Ставится цель урока, намечаются пути её достижения и указываются критерии её достижения.
2. Формирование новых знаний (лекция)
Линзы, основные точки, линии. Собирающие и рассевающие линзы.
Определения:
Линза (обычно изготавливаются из стекла);
Тонкая линза – линза, толщина которой значительно меньше радиусов ограничивающих её сферические поверхности;
Выпуклая, вогнутая линзы;
Главная оптическая ось;
Оптический центр линзы;
Главный фокус;
Фокальная плоскость;
Фокусное расстояние;
Рассеивающая, собирающая линзы;
Побочная оптическая ось.
Прозрачные тела, ограниченные двумя сферическими поверхностями (хотя бы одной…), называются линзами.
| 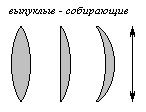 Середина толще, чем края. |  Середина тоньше, чем края. |
| 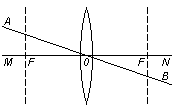
| Геометрические характеристики тонкой линзы: О – оптический центр линзы; MN – главная оптическая ось; F – главные фокусы линзы; Пл. F – фокальные плоскости; АВ – побочная оптическая ось (их множество). |
Оптическая сила линзы, единица измерения.
Оптическая сила линзы.
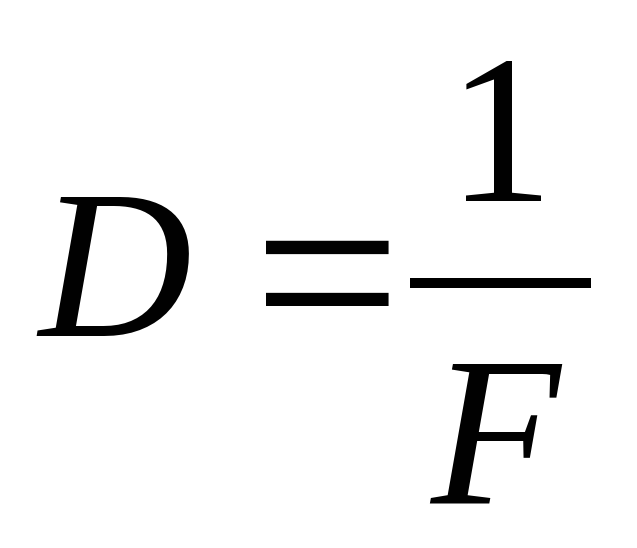
1 дптр (диоптрий) →F=1 м
Построение изображений, даваемых линзами. Построить на доске и в теради.
| Построение изображений в линзах. 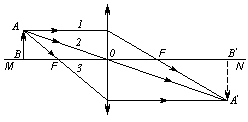
1. Луч, || главной оптической оси после преломления проходит через фокус линзы. 2. Луч, проходящий через оптический центр не преломляется. 3. Луч, проходящий через фокус после прохождения через линзу становится || главной оптической оси. | d F | увеличенное | прямое | мнимое | | F d F | увеличенное | перевернутое | действительное | | d 2F | уменьшенное | перевернутое | действительное | | d = 2F | натуральное | перевернутое | действительное |
|
| Построение изображения в рассеивающей линзе (изображение всегда мнимое). 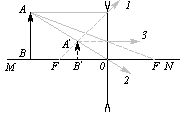 |
|
Построение изображения точки лежащей на главной оптической оси.

Демонстрации. Преломление света в линзах. Используется прибор для изучения законов геометрической оптики.
Формула тонкой линзы.

d – расстояние от предмета до линзы,
f – расстояние от линзы до изображения.

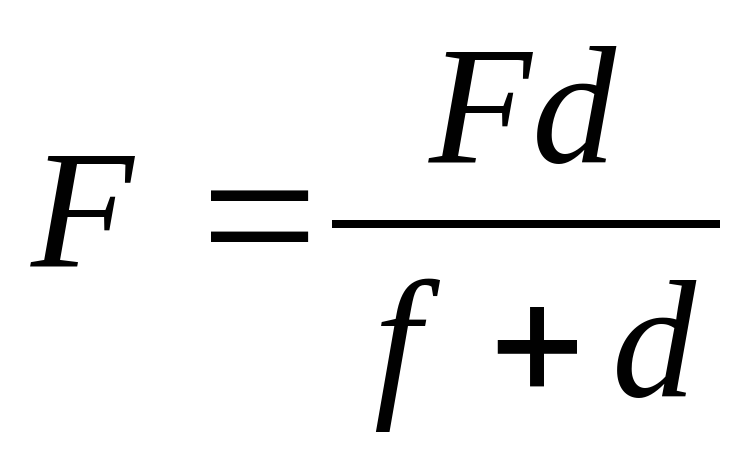 ;
; 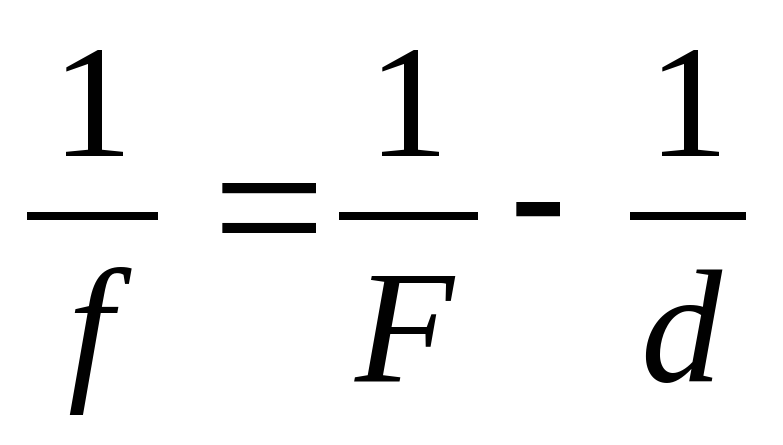 ;
; 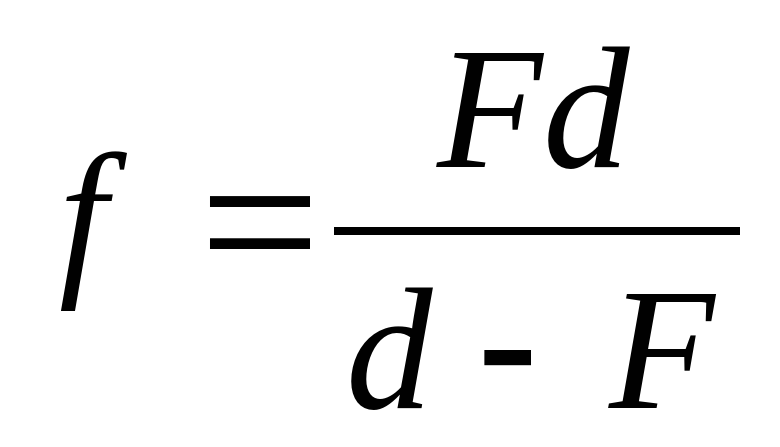
Для рассеивающей линзы F и f нужно брать со знаком «минус»
Линейное увеличение.
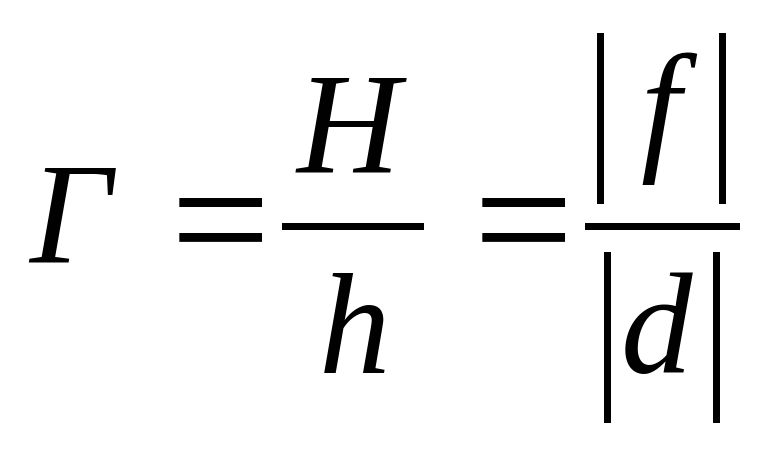
Н – высота изображения,
h – высота предмета.
4. Самостоятельное построение учащимися для случаев
F d F, d = 2F, d 2F
5.Домашнее задание. § 70-72, упр. 31 (3,4,5,6)
3















 ;
;  ;
;