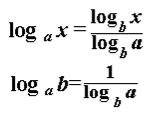Логарифм и его свойства

Логарифм и его свойства

Итак, давайте рассмотрим степенную функцию. Например, что значит 4² = 16? 2 - это показатель степени, который показывает, сколько раз необходимо умножить число 4 само на себя, чтобы получить 16. Иными словами, в какую степень следует возвести 4, чтобы получить 16. Если нам необходимо получить число 36 из числа 6, это значит, что мы число 6 должны возвести во вторую степень.

В общем виде рассматриваемые случаи можно записать следующим образом:

a^x = N.

Стоит обратить внимание, что в качестве "а" мы можем использовать все положительные числа, кроме числа 1. Более того, если число "а" больше нуля, то и N не может иметь отрицательные значения при любых показателях степеней.

Корнем некоторого уравнения a^x = N, где "а" может принимать положительные значения, отличные от нуля и единицы, является логарифмом некоторого N при основании "а". Иными словами,

ОПРЕДЕЛЕНИЕ: Логарифм - это степень, в которую необходимо возвести число "а", чтобы получить N.

Логарифм записывается словом log.

Например, 4³ = 64 можно записать иначе: log₄64 = 3.

Число 4 в данном логарифме называется его основанием. Данное выражение читается, как логарифм 64 по основанию 4 равен 3.

То есть для a^x = N, при "а" больше нуля и не равном единице, получим: log_aN = x.

На графике логарифм имеет вид, симметричный показательной функции.

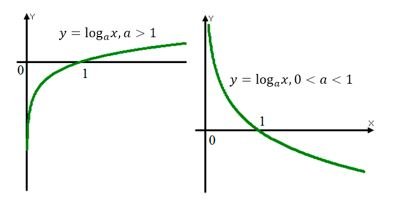
Свойство логарифмов для положительного "а", не равного единице

Логарифм имеет любое положительное число, отличное от единицы. Если число отрицательное, то оно не может иметь логарифма.

Обратите внимание на график, функция может принимать положительные, отрицательные значения, а также число ноль, но при этом х только стремится к нулю, не достигая его.

Свойства для функций, у которых "а" строго больше единицы

1. Если некоторое число N₁  N₂, то и log_aN₁  log_aN₂. То есть, чем больше число логарифма с одинаковыми основаниями, тем больше и значение логарифма.

2. Если логарифм записан для N  1, то значение логарифма положительное число. Если же N лежит в пределах от нуля до 1, то значение логарифма будет отрицательным числом.

3. При возрастании числа под логарифмом с одинаковым основанием должно возрастать и значение логарифма.

4. Если значения числа приближается к нулю, это значит, что значение логарифма убывает и может быть отрицательным. Чем больше модуль отрицательного значения логарифма, тем меньше число, и тем ближе оно к нулю.

Свойства для логарифмов, для которых "а" находится в пределе от нуля до единицы

1. Если некоторое число N растет, то значение логарифма падает.

2. Если число N больше единицы, то значение такого логарифма при заданном "а" будет числом отрицательным. Если же число N меньше единицы, то значение такого логарифма положительно.

3. Если число при заданном "а" возрастает до бесконечности, то значение такого логарифма падает до минус бесконечности.

Основное логарифмическое тождество

Среди всех остальных формул существует основное тождество, которое приводит к получению остальных свойств:

Свойства логарифмов

1. Если имеется логарифм произведения двух чисел больших нуля, то данный логарифм можно записать в виде суммы:

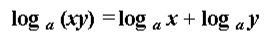
Данное свойство вытекает из основного свойства степени - при умножении степеней их показатели складываются.

2. Логарифм частного двух чисел равен разности двух логарифмов:

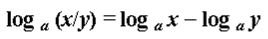
Данное свойство было получено из свойства деления степеней - при делении степеней, показатели вычитаются.

3. Если некоторое число в степени находится под знаком логарифма, то показатель степени можно вынести вперед, тем самым, умножив логарифм на показатель:

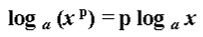
Данное свойство вытекает из одного из основных свойств степенной функции - при возведении степени в степень показатели степеней перемножаются.

4. Если число и основание логарифма совпадает, то значение такого логарифма равно единице:

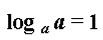
5. Логарифм по любому основанию равен нулю, если число равно единице:

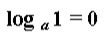
6. При любом логарифме можно перейти от одного основания к другому. Для этого необходимо просто воспользоваться формулами:

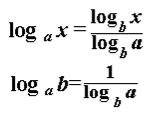
Десятичный и натуральный логарифмы, число е

Одним из самых распространенных логарифмов является десятичный логарифм. Данная функция имеет в основании число 10.

Десятичный логарифм используется для стандартной записи числа, ведь именно при данной записи число 10 возводится в некоторую положительную или отрицательную степень.

Десятичный логарифм записывается, как lg. 

Например, log₁₀100 = lg100 = 2.

Одним из основных видов логарифмов считается натуральный логарифм, который имеет в качестве основания иррациональное число, которое называется числом Эйлера. Данное число равно: е ≈ 2,718.

Если логарифм имеет основание "е", то такой логарифм называется натуральным или неперовым. Записывается он как ln.

Первая буква обозначения говорит о том, что это логарифм, а вторая - что он натуральный.

Наиболее распространенные натуральные логарифмы:

ln 2 = 0, ln 3 = 1,098, ln 10 = 2,303.

Все свойства, которые рассматривались в предыдущих вопросах для логарифмов, справедливы для десятичного и натурального логарифмов.