A10 .осн понятия и з-ны мат.логики (А15 ЕГ 2011)
преобразование и проверка истинности логич_выражений
1.Логическое выражение
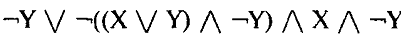
мах упрощается до а)
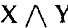
б)
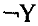
с)

д)
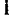
2. Какой логической функции соотв следующая таблица истинности
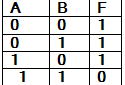
а.
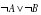
б.
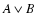
в.
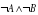
г.
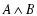
3. Выраж не (4X2 +9Y2 36) или ((X +Y)2 4)) и (Y2 |X+Y|) ложно при след знач набора перем: X=0, Y=0 X=-2, Y=1 X=1, Y=-1 X=0, Y=-2 X=-1,Y=-1
4.Даны 2 высказ А - «Студент сдал экзамены» В - «Студент едет на каникулы домой»
Сформул следующие высказывания:
1)Студ сдал экзамены И едет на каникулы домой, 2)Студ едет на каникулы домой, т к сдал экзамены 3студ) сдал экзамены, так как едет на каникулы домой 4)То, что студент сдал экзамены равносильно тому, что он едет на каникулы домой Чему соотв  ?
?
Какая из данных логических формул явл тождественно истинной?
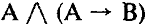
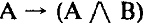
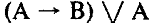
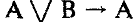
Какая из данных логических формул является тождественно ложной?
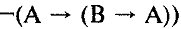
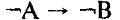
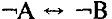
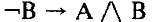
7. Сколько решений имеет система логических уравнений
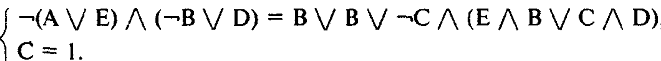
Сколько различных решений имеет система логических уравнений
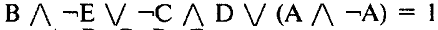
В ответе не надо перечислять все разные наборы зн A,B,C,D,E для которых оно верно
Каким усл польз для поиска информ в интернет об отдыхе в Сочи или в Адлере?
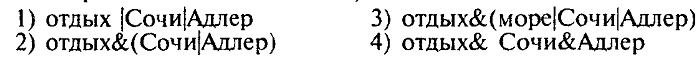
Для данной логической схемы значение F=0 невозможно для следующей
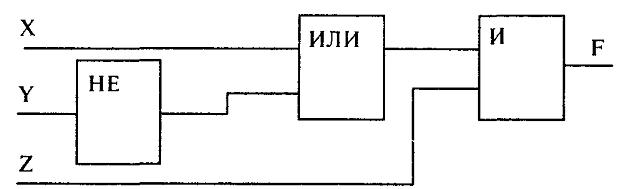
комбинации входных сигналов (X,Y,Z)
а) (0,0,1) б)(0,1,1) в) (1,0,0) г) (0,0,0)
9. Для данной логической схемы структурная формула имеет вид
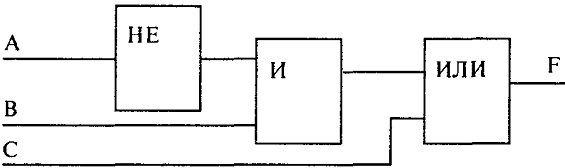

10. Высказ А, B,С истинны для всех точек, принадл соотв кругу, треугольнику, и прямоуг. Какое высказыв верно для выделенной на рис области?
A10. Какое из привед имён удовл логич условию:
(1я буква согласн → 2я буква соглас) /\ (предпосл буква гласная → последн буква гласная)?
1)КРИСТИНА 2)МАКСИМ 3)СТЕПАН 4)МАРИЯ
ЕГ. Преобр логич вызаж. Отрезки В4,А10 (2013,2012)
1) Каково наименьш нат число X, при кот истин выска (X • (X - 1) ((X - 1) * (X - 1) 80) ?
Обозн A= X • (X - 1) 80
Из 1го нер-ва получаем: X2-X где 
Из 2го получ:  X9.9 или
X9.9 или  где
где 
Значит  Выс
Выс истинно во всех сл кр Сл из истины не м след ложь, т к при
истинно во всех сл кр Сл из истины не м след ложь, т к при 
 сл то единст решение X=10
сл то единст решение X=10
2)Каково наиб целое число X, при кот ложно высказыв (9Х + 5 60) - (X • X 80) ? Отв:8
ЕГ2013
1)На числ прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Выб такой отрезок A, что ф-ла
( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q) тожд истинна, т е прин зн 1 при любом зн перем х.
1)[0, 3] 2)[3, 11] 3)[11, 15] 4)[15, 17]
Реш. Рассм интервал P=[2,10]. Оч, что обл истинности выр : x ∈ P предст отрезок на числ оси:
Обл истинности выр : x ∉ P — это объед инт-лов 
Для реш задач нам б нужны 2опер с инт=лами: пересеч (опред общей части 2 инт=лов) и объед. Если ввести высказ  то пересеч инт=лов P и Q опр обл истинности выр
то пересеч инт=лов P и Q опр обл истинности выр  (она выдел желтым цветом) (рис.1) Объед отрезков P и Q опред обл истинности логич суммы
(она выдел желтым цветом) (рис.1) Объед отрезков P и Q опред обл истинности логич суммы  (x принадл хотя бы 1из отрезков):
(x принадл хотя бы 1из отрезков):
Рис.1 рис.2
Для преобр логич выр нам Б нужна формула, представля импликацию через опер “ИЛИ” и “НЕ”
 и законы де Моргана:
и законы де Моргана: 
 т. Е если
т. Е если  то
то  т.е
т.е  отв 2
отв 2
2 способ Решим ур: ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=1 методом подстановки. В ур вместо P, Q впишем сами отрезки: [2, 10] и [6, 14]. (x ∈ А)=1 для всех вариантов.
| Вар
ответа | Интервал A | Зн x для проверки
(границы интервала) | ((x ∈ А) → (x ∈ [2, 10]) ) \/ (x ∈ [6, 14]) |
| 1 | [0, 3] | 0,3 | (1→0)V0=0 (1→1)V0=1 |
| 2 | [3, 11] | 3,11 | 1 (1→0)V1=1 |
| 3 | [11, 15] | 11, 15 | 1 (1→0)V0=0 |
| 4 | [15, 17] | 15,17 | 0 (1→0)V0=0 |
2) Для какого из приведенных чисел X логическое условие истинно?
((X21))
А)21 б)22 в)23 г)24
3) Для какого из приведенных чисел X логическое условие истинно?
ЕГ. Преобр логич вызажений. Логические высказывания
((X23)) → ((X15)) А)11 б)12 в)13 г)14
4) Какое из привед имён удовл логич усл:
(1я буква согл → 2я буква согл) &(предпосл буква гласная → последняя буква гласная)?
а) КРИСТИНА б) МАКСИМ в) СТЕПАН г) МАРИЯ
Общий подход:
Для каждого имени составить логич высказ и посмотр зн какого высказыв истинное.
а) КРИСТИНА (1→ 1) & (0→1) = 1 б) МАКСИМ (1→ 0) & (1→0) = 0
в) СТЕПАН (1→ 1) & (1→0) = 0 г) МАРИЯ (1→ 0) & (1→1) = 0 Отв: 1) КРИСТИНА
5) Какое из приведённых имён удовл логическому условию:
(1я буква согла → последняя буква согл) /\ (1я буква гласная → последняя буква гласная)?
Если таких слов неск, укаж самое длинное из них. А) АННА б) БЕЛЛА в)АНТОН г)БОРИС
5) На числ прямой даны два отрезка: P=[20,30] и Q=[10,40]. Вы такой отрезок A, что формула
((x∈P)→(x∈A))∧((x∈A)→(x∈Q)) тождест истинна, т е приним знач1 при любом знач перем х.
1) Для какого имени истинно высказывание:
(Первая буква согласная → Вторая буква согласная) & Последняя буква гласная?
1) КСЕНИЯ 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ
2) Для какого имени истинно высказывание:
¬ (Последняя буква гласная → 1я буква согласная) & 2я буква согласная?
1) ИРИНА 2) АРТЁМ 3) СТЕПАН 4) МАРИЯ
3) Для какого слова истинно высказывание:
¬ (1я буква согласная → (2я буква согласная V Последняя буква гласная))?
1) ГОРЕ 2) ПРИВЕТ 3) КРЕСЛО 4) ЗАКОН
4) Для какого имени истинно высказывание:
(1я буква согл → 2я буква гласная) & Последняя буква согласная?
1) АЛИСА 2) МАКСИМ 3) СТЕПАН 4) ЕЛЕНА
5) Для какого названия реки ложно высказывание:
(2я буква гласн → Предпосл буква согл) 1я буква стоит в алфавите раньше третьей?
1) ДУНАЙ 2) МОСКВА 3) ДВИНА 4) ВОЛГА
Доп.упражнения
Упростите логические формулы
3) а)  б)
б)  4)а)
4)а)  б)
б) 
5) Х & У & ( Х & Х ) Х У & Z ( Х & Х ) ( Х Х )
6) (ХУ)&(ХУ) У&ХУ&Х Х&УХХ&У
ЕГ Построение табл истинности ЛВ. частично заполненные табл лв
1)Для табл истинности функции F известны знач только некот ячеек: Каким выражением м б F?
| | | |
| 1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7 2) x1∨¬x2∨x3∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7 4) x1 ∨ x2∨¬x3 ∨x4∨ x5∨ ¬x6 ∨ x7 | 1) x1 ∧ x2 ∧ x3 ∧ x4 ∧ x5 ∧ x6 ∧ ¬x7 2)¬x1∨¬x2∨ x3 ∨¬x4 ∨¬x5∨x6∨ ¬x7 3) ¬x1∧x2∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7 4) x1∨ x2 ∨ ¬ x3∨ ¬x4∨x5∨¬x6 ∨ x7 | 1) ¬x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ ¬x5 ∧ x6 2) x1 ∨ x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 3) x1 ∧ ¬x2 ∧ ¬x3 ∧ x4 ∧ ¬x5 ∧ ¬x6 4) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ x5 ∨ ¬x6 |
| | | |
| 1) x1∧x2∧x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7 2) x1∨¬x2∨x3∨¬x4∨¬x5∨ x6 ∨¬x7 3) ¬x1∧ x2∧ ¬x3∧x4 ∧ x5 ∧ x6 ∧ x7 4) x1∨ x2∨¬ x3∨x4∨ x5 ∨ ¬x6 ∨ x7\ | 1) x1∧x2 ∧ x3 ∧ x4 ∧ x5 ∧ x6 ∧ ¬x7 2) ¬x1∨¬x2∨x3∨¬x4∨¬x5∨x6∨ ¬x7 3) ¬x1∧x2 ∧¬x3 ∧x4∧x5∧¬x6 ∧ x7 4) x1∨x2∨¬ x3∨¬x4∨x5∨ ¬x6 ∨ x7 | 1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 2) x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 ∨ x6 3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 4) ¬x1 ∨ x2 ∨ x3 ∨ x4 ∨ x5∨¬x6дан |
ЕГ Построение табл истинности ЛВ. ЛВ с 3 переменными
Символом F обозн одно из указа ниже логич выражений от 3 аргум: X, Y, Z. Дан фрагмент табл истинно выражение F: Какое выражение соответствует F?
| | |
| 1) (0 ∧ Y) ∧ (X ≡ Z) 2) (1 ∧ Y) ∧ (X ≡ Z) 3) (0 ∨ ¬Z) ∧ (X ≡ Y) 4) (¬1 ∧ Y) ∧ (X ≡ Z) | 1) (0 ∧ Z) ∧ (X ≡ Y) 2) (0 ∨ ¬Z) ∧ (X ≡ Y) 3) (1 ∧ Z) ∧ (X ≡ Y) 4) ( ¬1 ∧ Z) ∧ (X ≡ Y) |
| | |
| 1) ¬X ∧ ¬ Y 2) (X ≡ Y) ∧ Z 3) (X ≡ Y) ∨ Z 4) (¬X ≡ Y) ∨ Z | 1) ¬X ∨ ¬Y ∨ ¬Z 2) ¬X ∧ ¬Y ∧ ¬Z 3) X ∧ Y ∧ ¬Z 4) X ∨ Y ∨ Z |
ЕГ Построение табл истинности ЛВ. ЛВ с более чем с 3 переменными
1)Дано логическое выражение, зависящее от 5 логических перем. z1 ∧ ¬z2 ∧ ¬z3 ∧ ¬z4 ∧ z5
Сколько существует разли наборов значений перем, при кот выраж ложно?
1) 1 2) 2 3) 31 4) 32
2) Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F?
| | |
| 1) x1∨x2∨x3∨¬x4∨ ¬x5 2)¬x1∨x2 ∨¬x3 ∨x4∨¬x5 3) x1∧ ¬x2 ∧x3∧¬x4 ∧x5 4) ¬x1∧x2 ∧x3 ∧x4∧ ¬x5 Отв 4 | 1) x1 ∨ x2 ∨ x3∨ ¬x4 ∨¬x5 ∨¬x6 2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4∨¬x5 ∨ ¬x6 3) x1 ∧ x2 ∧ ¬x3 ∧ ¬x4∧ x5 ∧ x6 4) ¬x1 ∧ ¬x2 ∧ x3 ∧ x4 ∧ x5 ∧ x6 Отв 2 |
| | |
| 1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6) 2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1) 3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) 4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6) Отв 3 | 1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6) 2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1) 3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) 4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6) Отв 2е 2 № 6974 |
| | |
| 1) (х1 — х2) ∧ ¬хЗ ∧ х4 ∧ ¬х5 ∧ хб ∧ ¬х7 ∧ х8 2) (х1 — х2) ∨ ¬хЗ ∨ х4 ∨ ¬х5 ∨ хб ∨ ¬х7 ∨ х8 3) ¬(х1 — х2) ∨ хЗ ∨ ¬х4 ∨ х5 ∨ ¬хб ∨ х7 ∨ ¬х8 4) ¬(х1 — х2) ∧ хЗ ∧ ¬х4 ∧ х5 ∧ ¬хб ∧ х7 ∧ ¬х8 Отв 4 | 1) (х1 — х2) ∧ ¬хЗ ∧ х4 ∧ ¬х5 ∧ хб ∧ ¬х7 ∧ х8 2) (х1 — х2) ∨ ¬хЗ ∨ х4 ∨ ¬х5 ∨ хб ∨ ¬х7 ∨ х8 3) ¬(х1 — х2) ∨ хЗ ∨ ¬х4 ∨ х5 ∨ ¬хб ∨ х7 ∨ ¬х8 4) ¬(х1 — х2) ∧ хЗ ∧ ¬х4 ∧ х5 ∧ ¬хб ∧ х7 ∧ ¬х8 Отв 1 |







 а.
а. 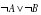 б.
б. 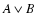 в.
в. 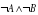 г.
г. 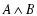
 ?
?























