Просмотр содержимого документа
«Mantiqiy amallar va ifodalar mavzusiga dars ishlanma.»
Mantiqiy amallar
(8-sinf)
Darsning texnologik xaritasi
|
Mavzu
|
Mantiqiy amallar
|
|
Maqsad va vazifalar
|
Darsning maqsadi: o‘quvchilarga mantiqiy amallar va sodda mulohazalar hamda mantiqiy qiymatlar haqida ma’lumot berish.
Darsning ta’limiy vazifasi: O‘quvchilarga mantiqiy amallar: «YOKI» -mantiqiy qo‘shish, «VA» - mantiqiy ko‘paytirish, «EMAS»-mantiqiy inkor haqida, sodda mulohazalar hamda «rost» yoki «yolg‘on» mantiqiy qiymatlar haqida tushunchalar berish.
Darsning tarbiyaviy vazifasi: o’quvchilarni yangi bilimlar egallashga va fikrlash qobiliyatlarini rivojlantirishga yo’naltirish.
Darsning rivojlantiruvchi vazifasi: o‘quvchilarning kompyuterdan foydalanish haqidagi bilim va tasavvurlarini kengaytirish va mantiqiy fikrlash darajasini kengaytirish.
|
|
O‘quv jarayonining mazmuni
|
Mantiqiy amallar: «YOKI»-mantiqiy qo‘shish, «VA»- mantiqiy ko‘paytirish, «EMAS»-mantiqiy inkor. Sodda mulohazalar. «Rost» yoki «yolg‘on» mantiqiy qiymatlar. Rostlik jadvallari. Vatandoshimiz Farobiyning bilish va mantiq ilmi yo’nalishidagi izlanishlari haqida qisqacha tarixiy ma’lumot.
|
|
O‘quv jarayonini amalga oshirish texnologiyasi
|
Uslub: Aralash.
Shakl: Savol-javob. Jamoa va kichik guruhlarda ishlash.
Vosita: Elektron resurslar, darslik, plakatlar; tarqatma materiallar.
Usul: Tayyor prezentatsiya va slayd materiallari asosida.
Nazorat: Og‘zaki, savol-javob, muhokama, kuzatish.
Baholash: Rag‘batlantirish, 5 ballik reyting tizimi asosida.
|
|
Kutiladigan natijalar
|
O’quvchilar yangi bilim va ko’nikmaga ega bo’ladi. Mantiqiy amallar: «YOKI»-mantiqiy qo‘shish, «VA»- mantiqiy ko‘paytirish, «EMAS»-mantiqiy inkor, sodda mulohazalar, «rost» yoki «yolg‘on» mantiqiy qiymatlari, rostlik jadvallari haqida bilim oladilar va ularni qo’llash ko’nikmalarini egallaydilar. Farobiy haqida tarixiy ma’lumotga ega bo’ladi. Mantiqiy amallarga doir misollar yechish makakasi shakllanadi.
|
|
Kelgusi rejalar (tahlil, o‘zgarishlar)
|
O’qituvchi o’z faoliyatining tahlili asosida yoki hamkasblarining dars tahlili asosuda keyingi darslariga o‘zgartirishlar kiritadi va rejalashtiradi.
|
Izoh: Qo’llanmada interfaol uslublar uchun quyidagicha belgilashlar qo’llanilgan.
M – ma’ruza, AH – aqliy hujum, K – klaster, BST – blits-savol-test, SJ – savol-javob, MY – mashq bajarish yoki misol va masala yechish.
Asosiy tushunchalar:
Mantiqiy qo‘shish, mantiqiy ko‘paytirish, mantiqiy inkor, mulohazalar, mantiqiy qiymatlar.
Darsning blok-chizmasi
|
|
Dars bosqichlari
|
Vaqt
|
|
|
1
|
Tashkiliy qism
|
3 minut
|
|
|
2
|
O‘tilganlarni takrorlash
|
7 minut
|
|
|
3
|
Yangi mavzu ustida ishlash
|
17 minut
|
|
|
4
|
Yangi mavzuni mustahkamlash
|
15 minut
|
|
|
5
|
Uyga vazifa
|
3 minut
|
|
O’tilganlarni qisqacha takrorlash quyidagicha amalga oshirish mumkin.
SJ, K Avvalgi mavzulardagi materiallar asosida.
BST Bobga doir testlar.
Mavzuni yoritish:
M Mulohazalar, asosan, matematikaning predmeti bo‘lib xizmat qiladi.
Mantiqiy amallar mulohazalar ustida bajarilib, ularning natijalari “ROST” yoki “YOLG‘ON” qiymatlaridan biriga teng bo‘lishi mumkin.
Mulohaza sifatida “ROST” yoki “YOLG‘ON”ligini aytish mumkin bo‘lgan ixtiyoriy gapni qarash mumkin. Masalan, “ikki karra ikki – to‘rt” – mulohaza bo‘ladi, chunki u rost, “Farg‘ona - Germaniyaning poytaxti” ham mulohaza bo‘ladi, chunki u yolg‘on. Ba’zan, “ROST” sifatida 1 va “YOLG‘ON” sifatida 0 yozishga odatlanilgan.
O’quvchilar “Mantiqiy qo‘shish”, “Mantiqiy ko‘paytirish” va “Mantiqiy inkor” amallari bilan tanishtiriladi.
Matematikada bu amallar uchun maxsus belgilar (nomlar) qabul qilingan.
Jumladan:
“Mantiqiy qo‘shish” - ( diz’yunksiya, “YOKI”, “+”)
“Mantiqiy ko‘paytirish” - “)( kon’yunksiya, “VA”, “
“Mantiqiy inkor” - ( inkor, “EMAS”, “ “) kabi belgilanadi.
“) kabi belgilanadi.
Bu amallar uchun quyidagi mantiq qonunlari o‘rinli:
|
Qonun
|
YOKI uchun
|
VA uchun
|
|
O‘rin almashtirish
|
x y = y x
|
x y= y x
|
|
O‘rinlashtirish
|
x( y z) = ( x y) z
|
x ( y z) = ( x y) z
|
|
Taqsimot
|
x ( y z) = ( x y () x z )
|
x ( y z) = ( x y () x z )
|
|
De Morgan qonuni
|
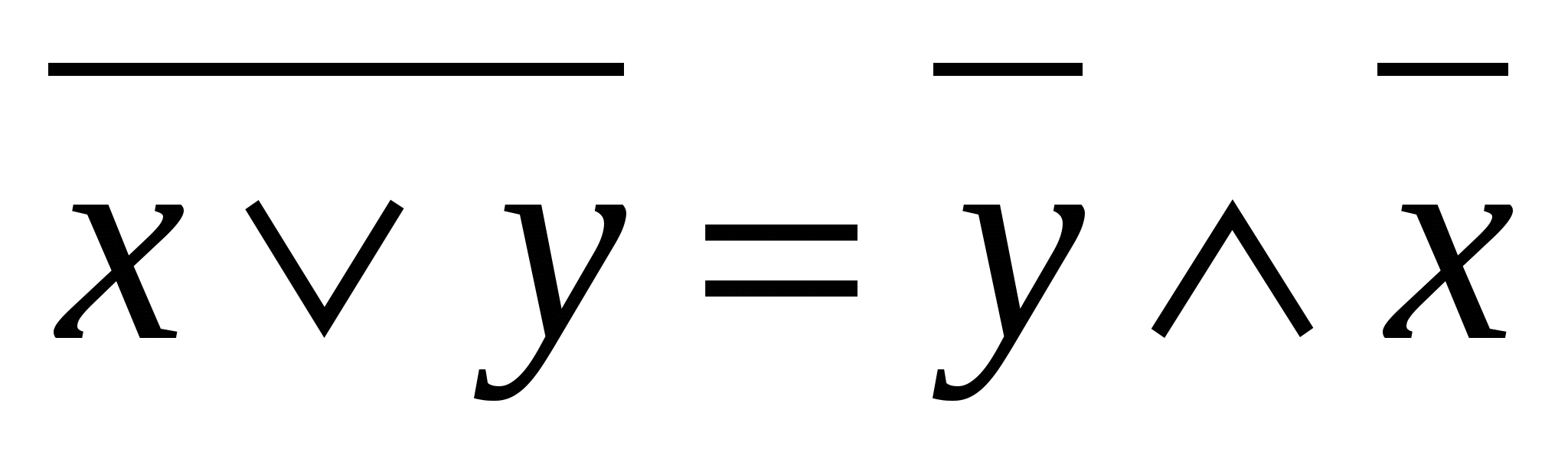
|
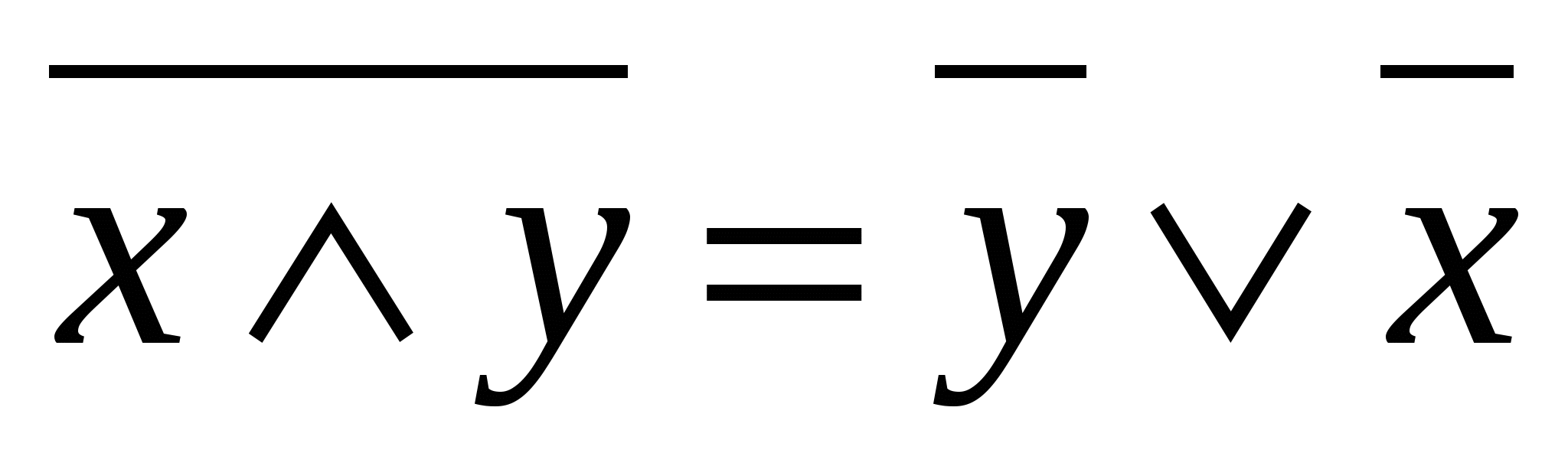
|
|
Idempotensiya
|
x x = x
|
x x= x
|
|
Yutilish
|
x ( x y) = x
|
x ( x y) = x
|
|
Ulanish
|
( x y () 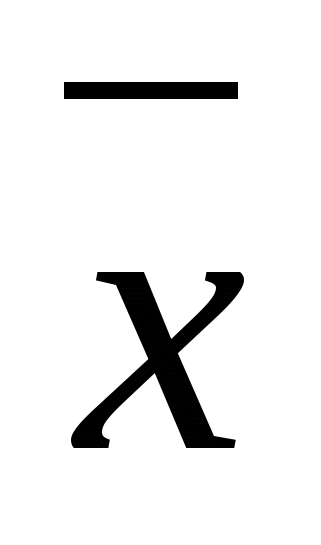 y ) = y y ) = y
|
( x y () 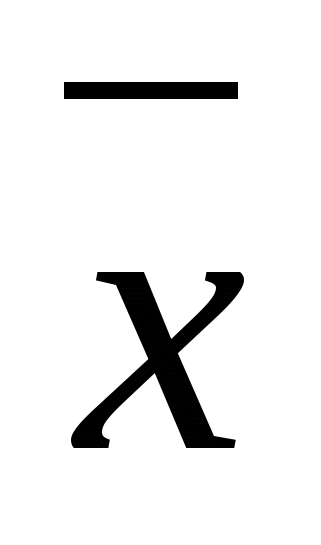 y ) = y y ) = y
|
|
O‘z aksi bilan amallar
|
x 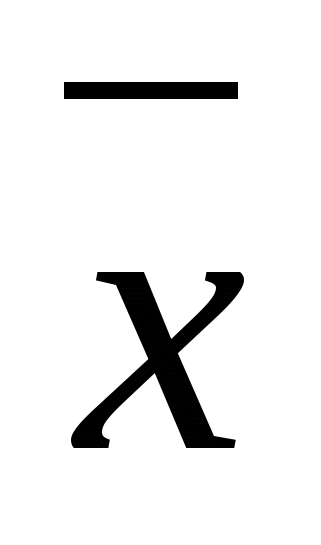 = 1 = 1
|
x 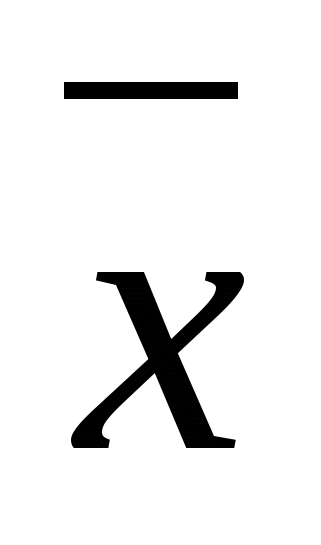 = 0 = 0
|
|
O‘zgarmaslar bilan amallar
|
x 0 = x , x 1 = 1
|
x 1 = x , x 0 = 0
|
|
Ikkilamchi inkor
|
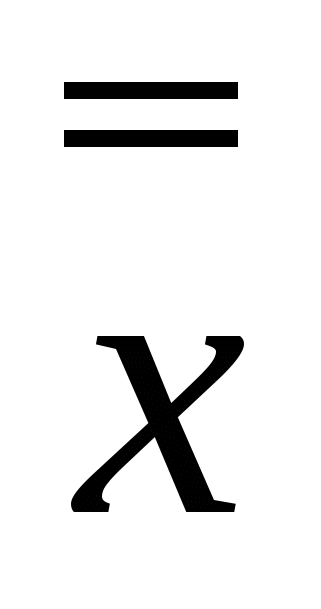 = x = x
|
AH O’quvchilar bilan quyidagi kabi misollar interfaol usulda yechiladi.
1-misol. Berilgan A, B, D, E o‘zgaruvchilarning qiymati A - rost, B - rost, D - yolg‘on, E- yolg‘on bo‘lganda quyidagi mantiqiy amal natijasi qanday bo‘ladi?
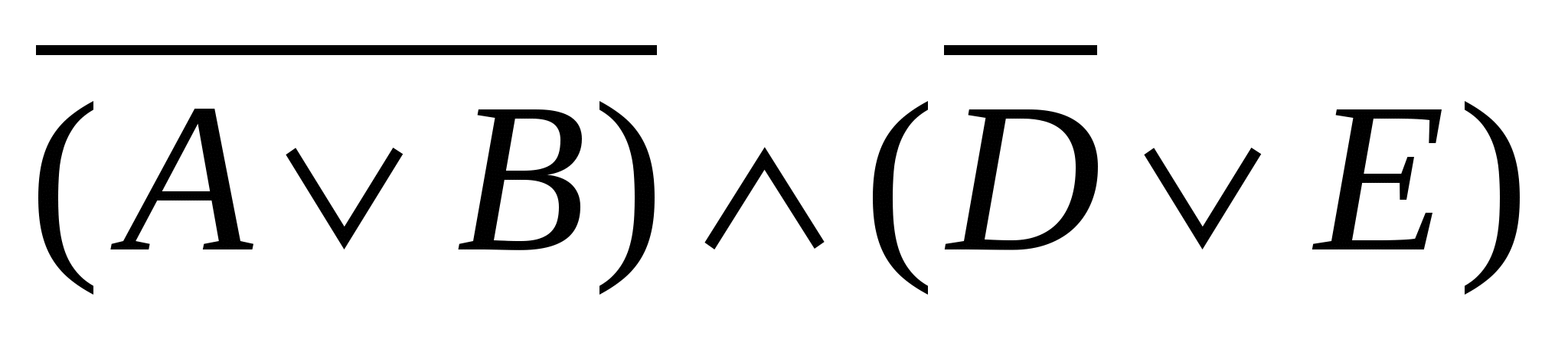
Yechish: B - rost, rostning inkori esa yolg‘on. Keyingi qavs ichidagi amalning natijasi qanday bo‘lishidan qat’iy nazar yolg‘on bilan ko‘paytmasi yolg‘on natija beradi. Demak, A-rost, B-rost bo‘lganda A javob: yolg‘on
2-misol. A – “Alisher 2-sinfda o‘qiydi” va B – “Alisher 8 yoshda” mulohazalar berilgan bo‘lsa, quyidagi mantiqiy ifodani so‘zlar orqali yozing:
А В
Yechish: Ifodada A va B mulohazalarning mantiqiy ko‘paytmasi berilgan. Mantiqiy ko‘paytma “va” bog‘lovchisiga mos kelgani uchun berilgan mantiqiy ifoda quyidagicha o‘qiladi:
Alisher 2-sinfda o‘qiydi va u 8 yoshda.
3-misol. Bir kishi “Men yolg‘onchiman va qora sochliman” dedi. U aslida kim?
Yechim. Shartdagi mulohazalar uchun belgilashlar kiritamiz:
D= “Men yolg’onchiman va qora sochliman”;
A= “Men yolg’onchiman”; B= “Qora sochliman”
Masala shartidagi mulohazani shunday yoza olamiz: D=A VA B. Bu amal uchun rostlik jadvali quyidagicha ko’rinishda bo’ladi:
|
A
|
B
|
D=A VA B
|
|
|
|
ROST
|
ROST
|
ROST
|
|
ROST
|
YOLG’ON
|
YOLG’ON
|
|
YOLG’ON
|
ROST
|
YOLG’ON
|
|
YOLG’ON
|
YOLG’ON
|
YOLG’ON
|
Masala yechimini topish uchun quyidagicha mulohaza yuritamiz:
a) agar A=YOLG’ON bo’lsa, u holda masala shartidagi mulohazani aytgan kishi rostgo’y bo’ladi va tabiiyki uning hamma gapi rost. Demak, D=ROST bo’lishi kerak. Lekin jadvaldan ko’rinadiki, A=YOLG’ON bo’lganda D=ROST bo’lolmaydi.
b) agar A=ROST bo’lsa, u holda masala shartidagi mulohazani aytgan kishi yolg’onchi bo’ladi va tabiiyki uning hamma gapi yolg’on. Demak, D=YOLG’ON bo’lishi kerak. Jadvaldan ko’rinadiki, bunday imkoniyat A=ROST va B=YOLG’ON bo’lsagina bor.
Javob: masala shartidagi mulohazani aytgan kishi YOLG’ONCHI va QORA SOCHLI EMAS ekan.
4-misol. a ning barcha butun sonli qiymatlarida a2≥ 0 mantiqiy ifoda qanday qiymatga ega bo‘ladi?
Yechish. Har qanday sonning juft (bizning holda, ikkinchi) darajasi manfiy emasligidan berilgan mantiqiy ifodaning qiymati doimo “rost” bo‘lishi kelib chiqadi.
Javob: Rost.
5-misol. (5 ( 8 3=6 3 1)) 67 mantiqiy ifoda qiymatni hisoblang.
Yechish. I usul:
Avval amallar bajarilish tartibini belgilab olamiz:
3 2 1 5 4 7 6
(5 ( 83=631)) 67
51 - rost
(51) - yolg‘on
(5 (1)) - rost
3=6 – yolg‘on3
(5 ( 3=6 - rost 3 1))
8 67 – yolg‘on
(5 ( 8 3=6 3 1)) 67 – rost
II usul:
(5 ( 3=63 1)) 8yolg‘on (yolg‘on) yol’gon yolg‘onrost) ( 67
rost. yolg‘on rost
Javob: rost
6-misol. 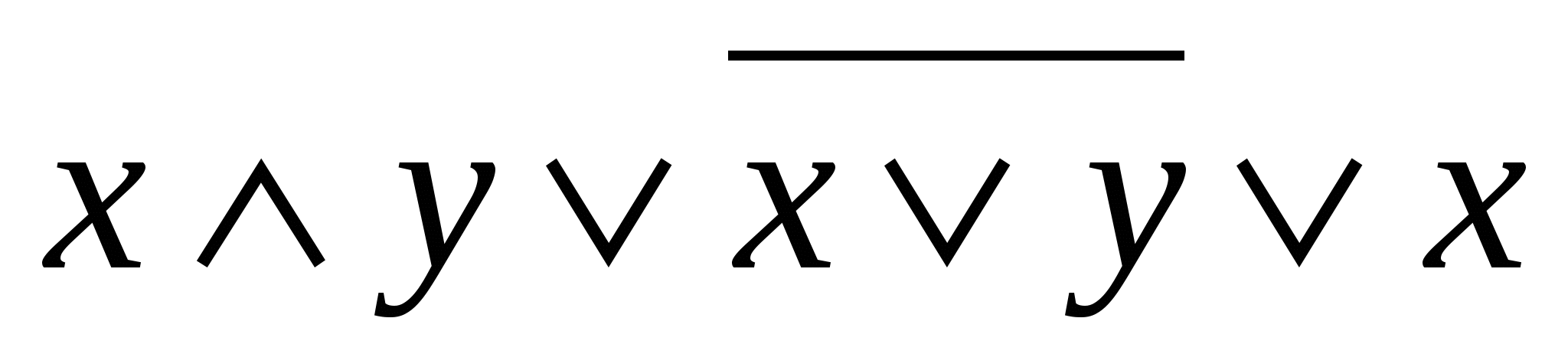 formula orqali berilgan mantiqiy mulohazaning rostlik jadvalini tuzing.
formula orqali berilgan mantiqiy mulohazaning rostlik jadvalini tuzing.
Yechish: Quyidagicha ketma-ketlik hosil qilamiz.
| O‘zgaruvchi | Oraliq mantiqiy formulalar | Yechim |
|
x
|
y
|
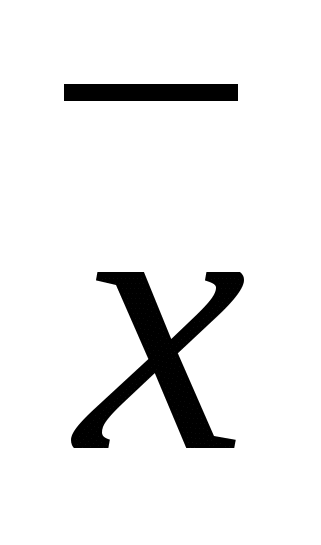
|
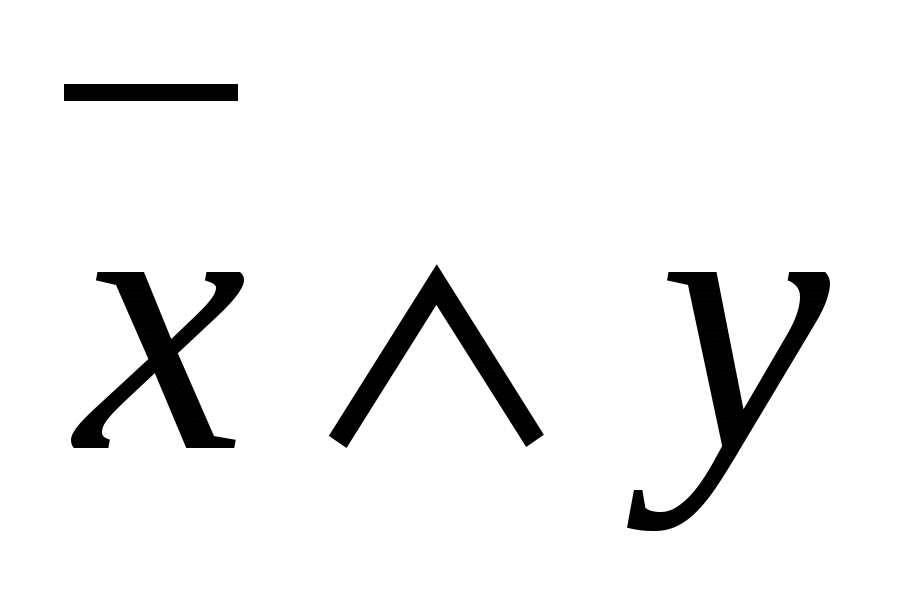
|
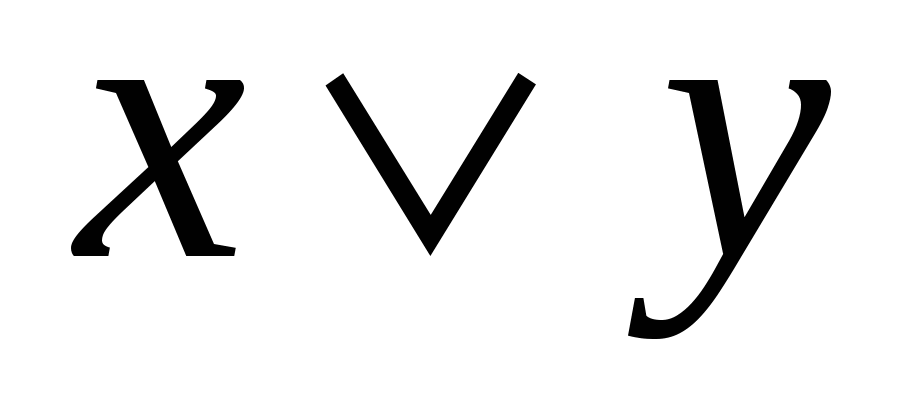
|
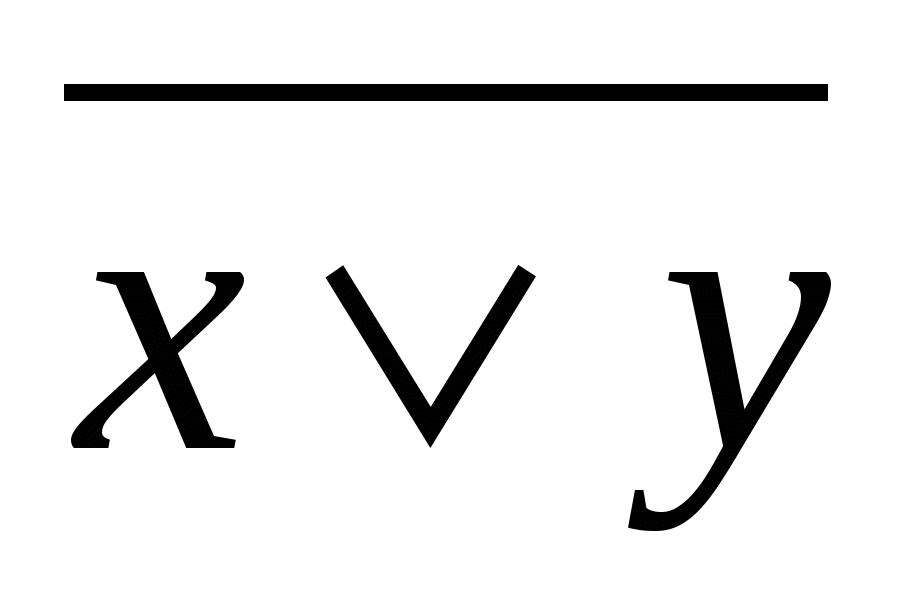
|
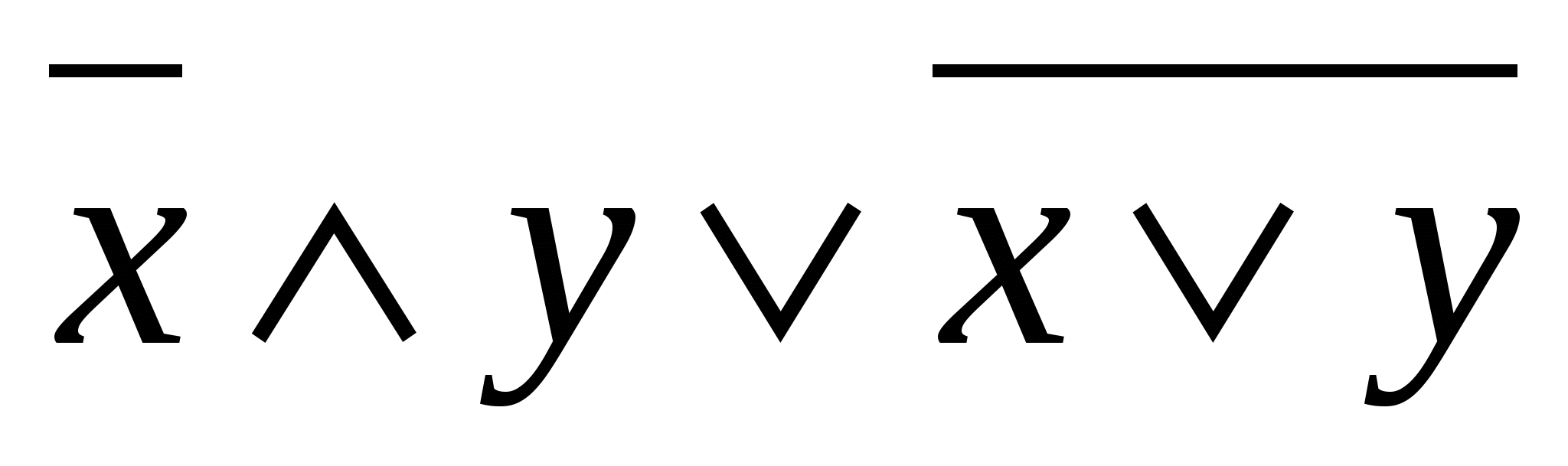
|
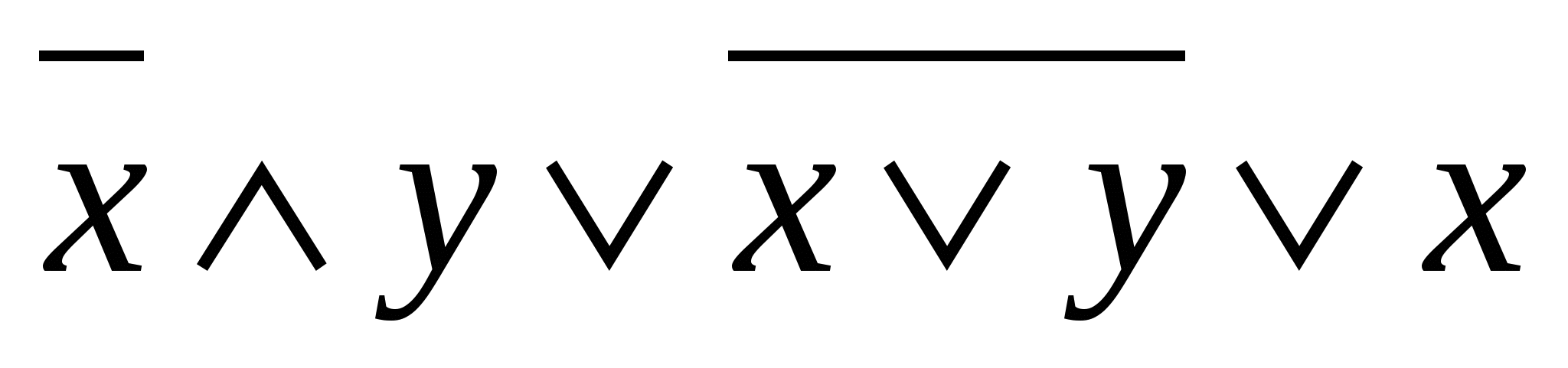
|
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
7-misol. 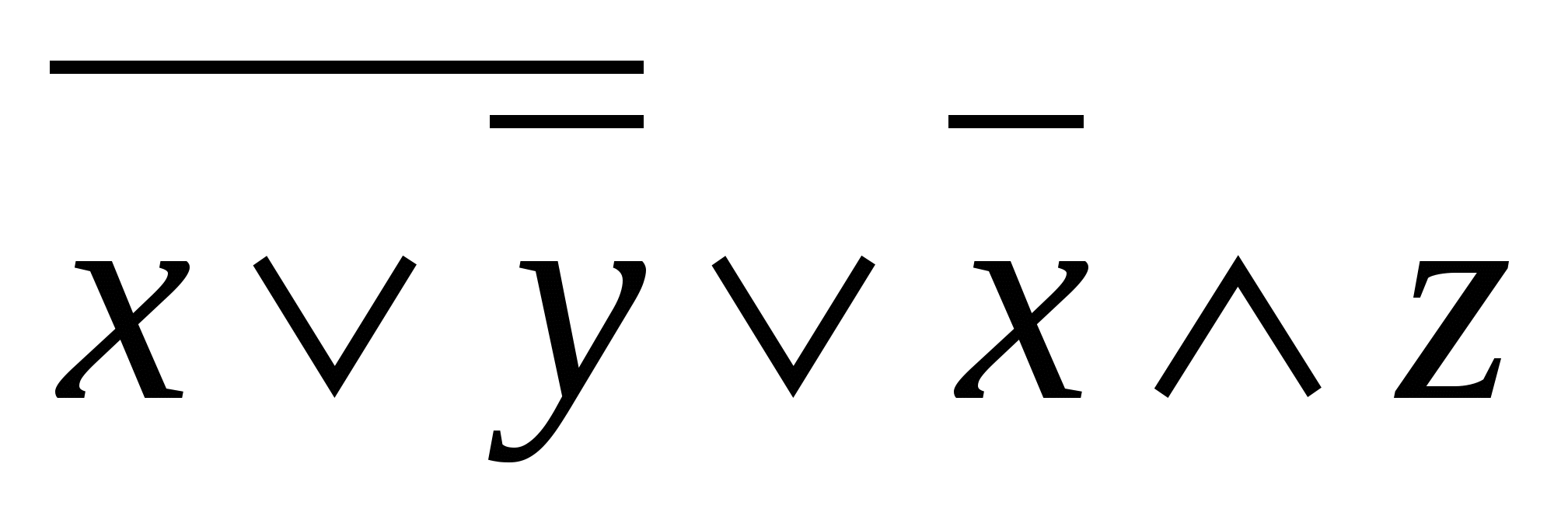 formula orqali berilgan mantiqiy mulohazaning rostlik jadvalini tuzing.
formula orqali berilgan mantiqiy mulohazaning rostlik jadvalini tuzing.
Yechish: Quyidagicha ketma-ketlik hosil bo‘ladi.
|
O‘zgaruvchi
|
Oraliq mantiqiy formulalar
|
Yechim
|
|
x
|
y
|
z
|
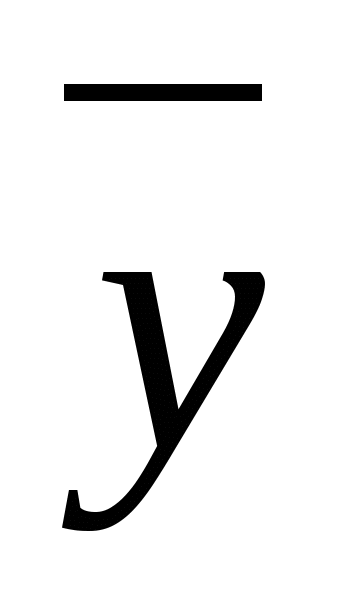
|
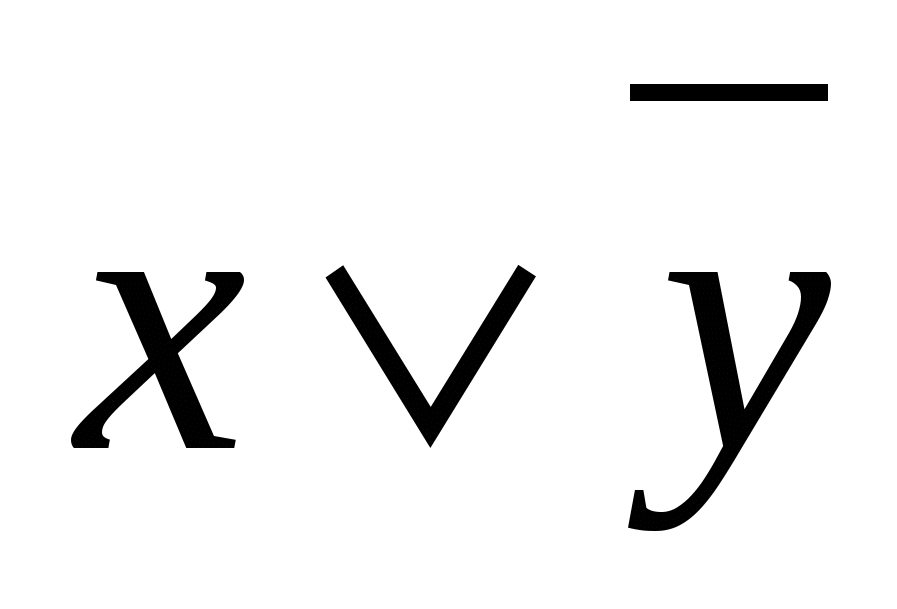
|
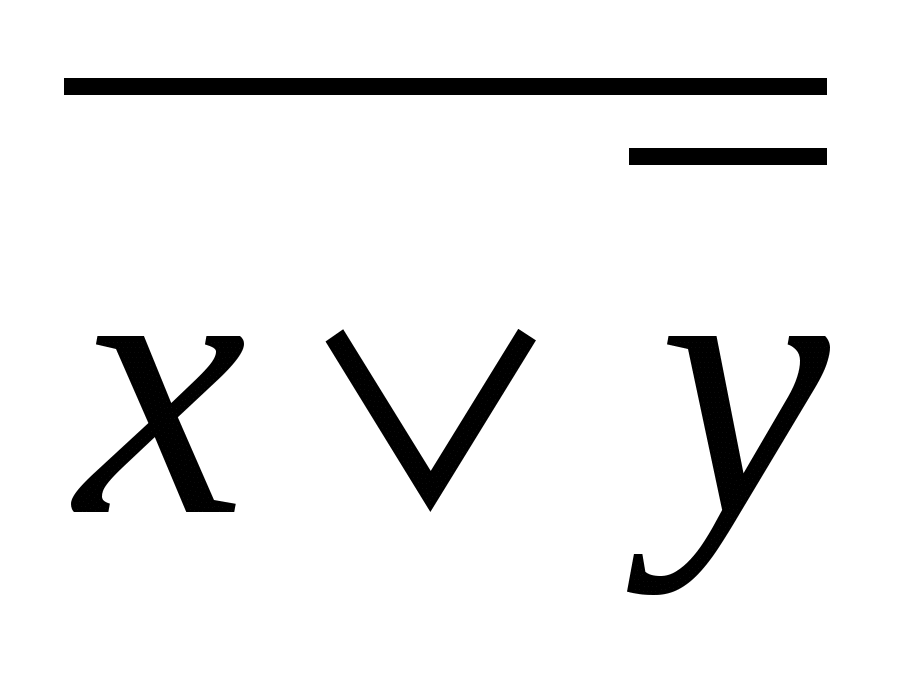
|
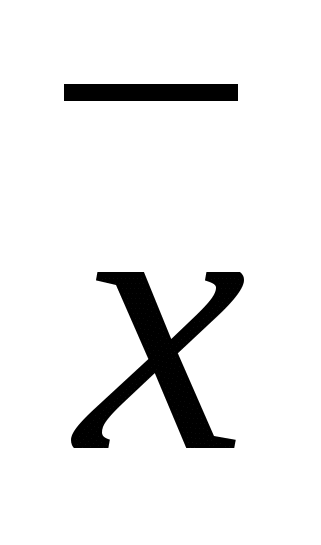
|
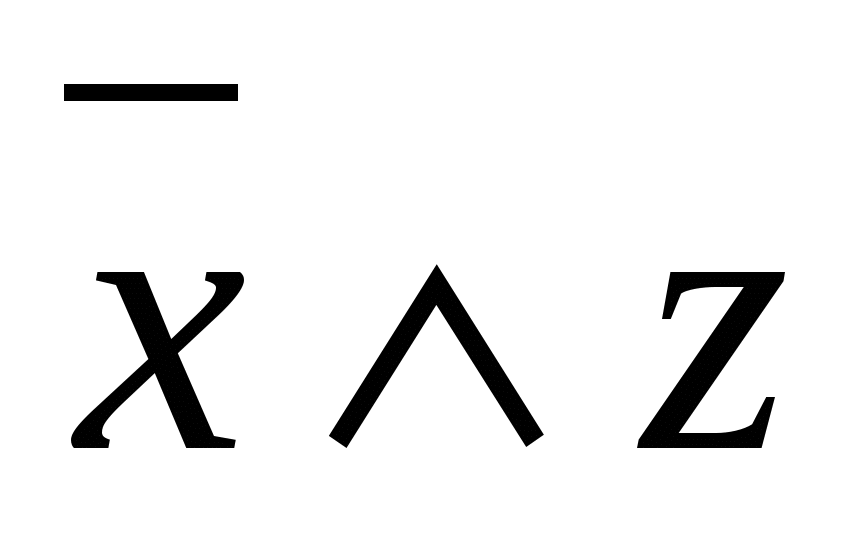
|
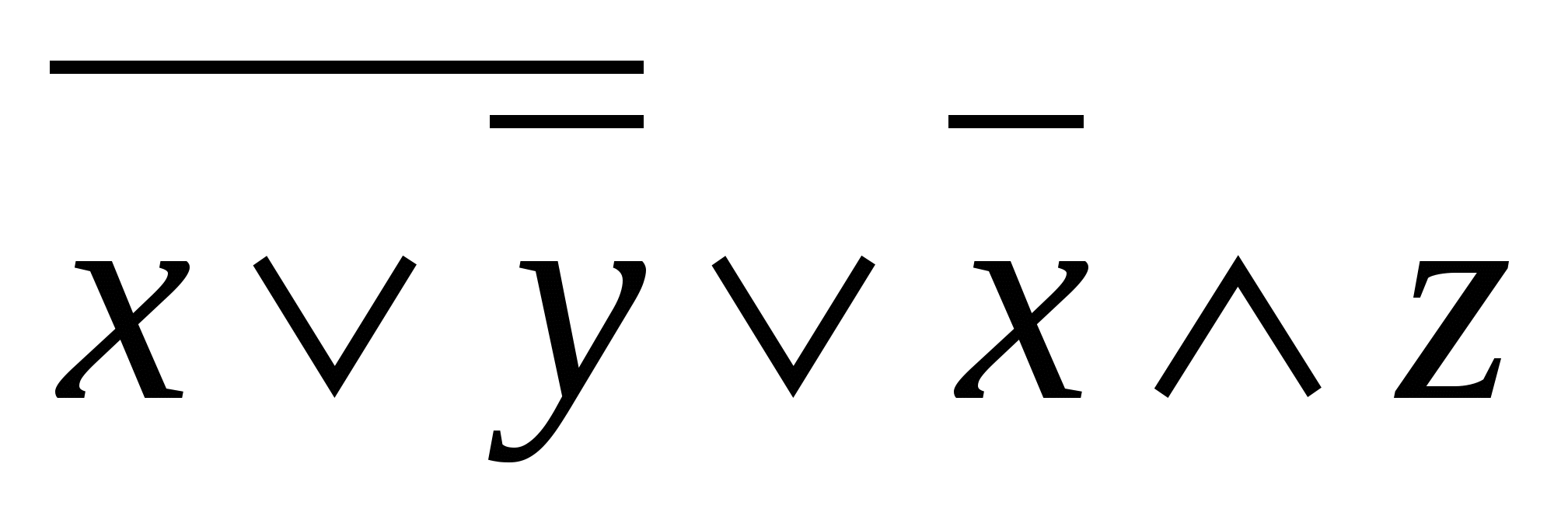
|
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
8-
 misol. y ). (x y Ifodani soddalashtiring: x
misol. y ). (x y Ifodani soddalashtiring: x
Yechish:
d 



 y ) (x y y ) = x (x y e Morgan qonuniga asosan: x
y ) (x y y ) = x (x y e Morgan qonuniga asosan: x
o 




 y y x y ) = x (x y ‘rinlashtirish qonuniga asosan: x
y y x y ) = x (x y ‘rinlashtirish qonuniga asosan: x
o 



 y y y = 0 y x ‘z aksi bilan amallar qonuniga asosan: x
y y y = 0 y x ‘z aksi bilan amallar qonuniga asosan: x
o 

 y = 0 y = 0 y ‘zgarmas bilan amallar qonuniga asosan: 0
y = 0 y = 0 y ‘zgarmas bilan amallar qonuniga asosan: 0
9-misol. t). z z y x z (x y Ifodani soddalashtiring: x
Yechish: De Morgan, ikkilamchi inkor va yutilish qonunlarini qo‘llaymiz:
t) = z z y x z (x y t) = x z z y x z (x y x
y . t = x z y x z y x y = x
10-misol. Uchta do’st futbol bo’yicha 2010-yilgi jahon chempionati natijalari haqida bahslashishardi.
“Mana ko’rasiz, Ispaniya chempion bo’lmaydi, Germaniya chempion bo’lishi aniq” – dedi Abror.
“Yo’g’e, Ispaniya chempion bo’ladi, Argentina haqida gapirmasa ham bo’ladi, u chempion bo’lolmaydi” – dedi Behzod.
“Germaniya chempionlikka yaqin ham kelmaydi, lekin Argentinada zo’r o’yinchilar bor” – dedi Muzaffar.
Chempionat tugagandan keyin esa qarashsa, uch do’stdan ikkitasini ikkala gapi ham to’g’ri, uchinchisini ikkala gapi ham noto’g’ri ekan. Kim chempiom bo’lgan?
Yechim. Ba’zi belgilashlarni kiritib olamiz:
A – Argentina chempion, G – Germaniya chempion, I – Ispaniya chempion.
Muzaffarning “Argentinada zo’r o’yinchilar bor” gapi kim chempion bo’lishi haqida xech qanday ma’lumot bermaydi, shuning uchun keyingi mulohaza yuritishimizga qaralmaydi. Har bir do’stni gapini belgilab olamiz:
Abror: (EMAS I ) VA G; Behzod: I VA (EMAS A); Muzaffar: EMAS G.
Do’stlarning ikkitasini ikkala gapi ham to’g’ri, uchinchisini ikkala gapi ham noto’g’ri ekanligini hisobga olib quyidagi D mulohazani hosil qilamiz:
D=((EMAS I ) VA G) VA (I VA (EMAS A)) VA (EMAS(EMAS G)) YOKI
((EMAS I ) VA G) VA (EMAS (I VA (EMAS A))) VA (EMAS G) YOKI
(EMAS ((EMAS I ) VA G)) VA (I VA (EMAS A)) VA (EMAS G)=ROST.
D mulohaza uchun rostlik jadvalini tuzib chiqib kim chempion bo’lganini bilib olish mumkin. Albatta, mantiq qonunlarini qo’llab D mantiqiy ifodani soddalashtirish osonroqdir.
Mavzuni mustahkamlash va yakunlash:
SJ Darslikdagi yoki qo’shimcha savol va topshiriqlar.
MY Darslikdagi 1-2-3-mashqlar yoki qo’shimcha vazifalar.
BST Testlardan namunalar:
1. Qaysi mantiqiy amal natijasi qiymati mulohaza yolg’on bo’lgandagina rost bo’ladi?
A) VA B) EMAS D) YOKI E) AMMO
2. Qanday mantiqiy amallar bor?
A) VA, YOKI B) EMAS D) LEKIN E) A va B
3. Qaysi mantiqiy amal natijasi qiymati ikkala mulohaza rost bo’lgandagina rost bo’ladi?
A) VA B) EMAS D) BIROQ E) YOKI
4. Qaysi mantiqiy amal natijasi qiymati mulohazalardan birortasi rost bo’lganda rost bo’ladi?
A) AMMO B) EMAS D) VA E) YOKI
5. Qaysi mantiqiy amal natijasi qiymati mulohaza rost bo’lgandagina yolg’on bo’ladi?
A) VA B) EMAS D) LEKIN E) YOKI
6. Qaysi mantiqiy amal natijasi qiymati mulohazalardan bittasi rost bo’lganda yolg’on bo’ladi?
A) VA B) BIROQ D) EMAS E) YOKI
7. Qaysi mantiqiy amal inventor sxemasiga mos keladi?
A) VA B) BIROQ D) EMAS E) YOKI
8. Qaysi mantiqiy amal mos tushish sxemasiga mos keladi?
A) VA B) BIROQ D) EMAS E) YOKI
Uyga vazifa:
1. Darslikdagi 4-mashq.
2. Test tuzish (5 ta va undan ortiq).
3*. Darslikdagi 5-mashq.

















