Мастер-класс «Нестандартные задачи»

Ход мастер-класса

Помашите рукой. Кто учился в школе? Помашите рукой. Кто любил математику?

Помашите рукой. Кто помнит, как звали учителя математики?

Я учитель математики – Киселева О.В. Предлагаю вам вернуться в детство.

Закройте глаза и вспомните своего учителя математики и свои уроки математики.

Чему вас учили на уроках математики? (ответы: считать, решать задачи…)

Со всеми ответами я согласна, но остановлюсь на одном: учили решать задачи.

Что развивают задачи? (логику, умение мыслить, творчество и т.д.)

Да, я согласна, и думаю, никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учеников. Роль математики в развитии логического мышления исключительно велика. Как показывает мой опыт, в школьном возрасте одним из эффективных способов развития мышления является решение школьниками нестандартных логических задач. Кроме того, решение нестандартных логических задач способно привить интерес ребенка к изучению «классической» математики. Через занимательность проникает в сознание ученика сначала ощущение прекрасного, а затем, при последующем систематическом изучении математики, и понимание красоты ее методов.

Что помогает мне:

1. Развивать познавательные навыки учащихся: умение самостоятельно конструировать свои знания, ориентироваться в информационном пространстве.

2. Развивать критическое и творческое мышление, умение увидеть, сформулировать и решить проблему.

3. Развитие у учащихся интереса к предмету;

4. Накопление определенного запаса математических фактов и сведений, умений и навыков, дополняющих и углубляющих знания, приобретаемые в основном курсе математики

Сегодня я покажу некоторые нестандартные задачи, которые я применяю на своих урока и во внеурочной деятельности.

Это задачи связанные с математическими парадоксами и софизмами.

Математический парадокс можно определить как истину, настолько противоречащую нашему опыту, интуиции и здравому смыслу, что в нее трудно поверить даже после того, как мы шаг за шагом проследим все ее доказательство.

Математическим софизмом принято называть не менее удивительные утверждения, в доказательствах которых в отличие от доказательства парадоксов кроются незаметные, а подчас и довольно тонкие ошибки.

Давайте проведем опыт:

Возьмите бумажную ленту АВСD. Прикладываем ее концы АВ и СD друг к другу и склеиваем. Но не как попало, а так, чтобы точка А совпала с точкой D, а точка B с точкой С. Получим такое перекрученное кольцо. И задаемся вопросом: сколько сторон у этого куска бумаги? (Две, как у любого другого?)

1 группа проверьте: попробуйте закрасить это кольцо с одной стороны. Красим, не отрываемся, на другую сторону не переходим. Красим... Закрасили? Сделайте вывод.

2 группа. Проверьте: что будет, если разрезать посередине это кольцо по всей длине? Разрежьте. Сделайте вывод.

3 группа. Проверьте: что будет, если разрезать его вдоль, но не посередине, а ближе к одному краю? Разрежьте. Сделайте вывод.

Исследуйте дальше эту поразительную (и тем не менее совершенно реальную) одностороннюю поверхность, и вы получите море удовольствия.

Эта удивительная поверхность называется лентой Мейбуса (немецкий математик).

Применение. Слайды. Лист Мёбиуса служил вдохновлением для скульптур и для графического искусства. Мауриц Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — лист Мёбиуса II, показывает муравьёв, ползающих по поверхности ленты Мёбиуса.

Лист Мёбиуса также постоянно встречается в научной фантастике, напр. в рассказе Артура Кларка Стена Темноты. Иногда научно-фантастические рассказы предполагают, что наша вселенная может быть некоторым обобщенным листом Мёбиуса. В рассказе «Лист Мёбиуса» автора А. Дж. Дейча, бостонское метро строит новую линию, маршрут которой становится настолько запутанным, что превращается в ленту Мёбиуса, после чего на этой линии начинают исчезать поезда.

Существовали технические применения ленты Мёбиуса. Полоса ленточного конвейера выполнялась в виде ленты Мёбиуса, что позволяло ему работать дольше, потому что вся поверхность ленты равномерно изнашивалась. Также в системах записи на непрерывную плёнку применялись ленты Мёбиуса (чтобы удвоить время записи). В матричных принтерах красящая лента также имела вид лист Мёбиуса для увеличения срока годности.

Устройство под названием резистор Мёбиуса — это недавно изобретенный электронный элемент, который не имеет собственной индуктивности. Никола Тесла запатентовал подобное устройство в начале 1900-ых, патент.

Сейчас я хочу показать, что такое софизмы. Как я уже сказала это утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Рассмотрим пример: (пальцы)

Задание в группам: найдите ошибку.

1 группа: Возьмем два произвольных неравных между собой числа а и в и запишем для них очевидное тождество

а2-2ав+в2=в2-2ав+а2

(а-в)2=(в-а)2

а-в = в-а

2а=2в

а=в

2 группа : 2*2=4

4:4=5:5

4(1:1)=5(1:1)

2*2(1:1)=5(1:1) = 2*2=5 = 4=5

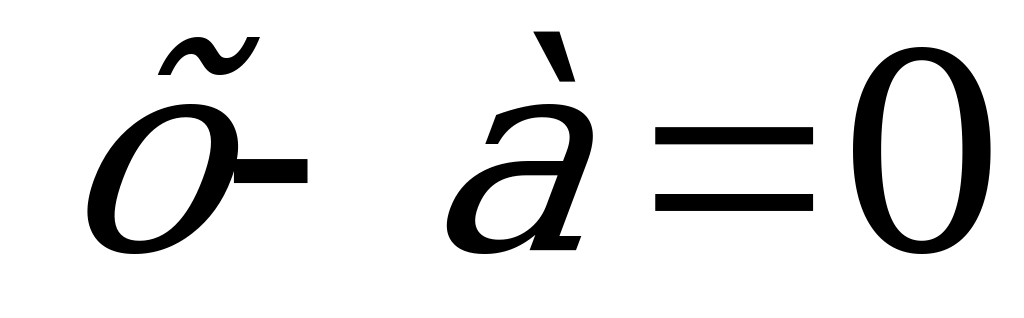
3 группа: Возьмем уравнение

Р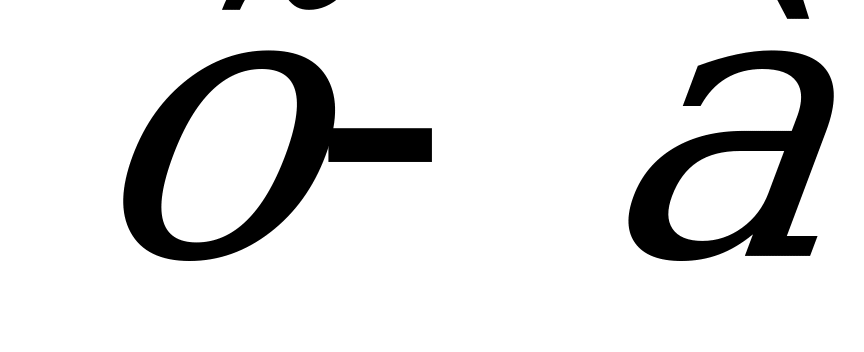 азделив обе части на , получим

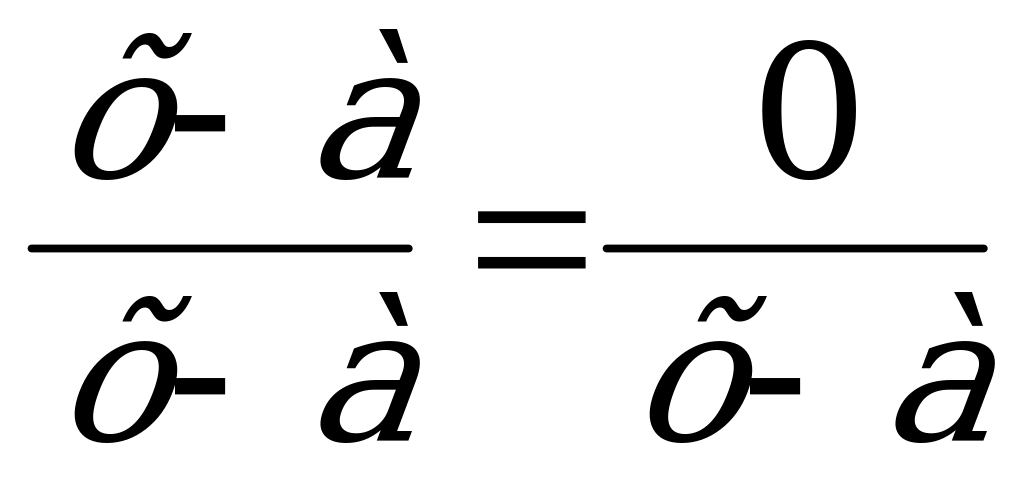
Откуда сразу получаем требуемое

равенство

1=0

4 группа: Запишем очевидное для любого

числа а тождество

а²-а² = а²-а²

Вынесем а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получив

а(а-а)=(а+а)(а-а)

Разделив обе части на а-а, получим а=а+а, или а=2а

Математических парадоксов и софизмов очень много и можно подобрать материал на любую тему математики.

Я думаю, что у вас появился интерес к математике. Спасибо вам за помощь.

Пусть все задачи, которые встают перед вами будут решены.

Благодарю за работу.

1 группа проверьте: попробуйте закрасить это кольцо с одной стороны. Красим, не отрываемся, на другую сторону не переходим. Красим... Закрасили? Сделайте вывод.

2 группа. Проверьте: что будет, если разрезать посередине это кольцо по всей длине? Разрежьте. Сделайте вывод.

3 группа. Проверьте: что будет, если разрезать его вдоль, но не посередине, а ближе к одному краю? Разрежьте. Сделайте вывод.

1 группа проверьте: попробуйте закрасить это кольцо с одной стороны. Красим, не отрываемся, на другую сторону не переходим. Красим... Закрасили? Сделайте вывод.

2 группа. Проверьте: что будет, если разрезать посередине это кольцо по всей длине? Разрежьте. Сделайте вывод.

3 группа. Проверьте: что будет, если разрезать его вдоль, но не посередине, а ближе к одному краю? Разрежьте. Сделайте вывод.

1 группа проверьте: попробуйте закрасить это кольцо с одной стороны. Красим, не отрываемся, на другую сторону не переходим. Красим... Закрасили? Сделайте вывод.

2 группа. Проверьте: что будет, если разрезать посередине это кольцо по всей длине? Разрежьте. Сделайте вывод.

3 группа. Проверьте: что будет, если разрезать его вдоль, но не посередине, а ближе к одному краю? Разрежьте. Сделайте вывод.