Муниципальное автономное общеобразовательное учреждение
«Светлинская средняя общеобразовательная школа №2»
п.Светлый Светлинский район Оренбургская область
МАСТЕР-КЛАСС
по теме «ДВИЖЕНИЕ ПО ОКРУЖНОСТИ»
Автор разработки учитель математики
Тюнева Надежда Васильевна
высшая квалификационная категория
п.Светлый
2021 г
Цели и задачи мастер-класса:
- показать различные способы решения текстовых задач на движение по окружности
- повышение уровня теоретической и методической подготовки участников;
- создать условия для профессионального самосовершенстования участников.
Принцип мастер-класса: «Я знаю, как это делать. Я научу вас».
Эпиграф :
«Математика это сложно,
но интересно и увлекательно!»
Ожидаемые результаты мастер-класса.
- Понимание его участниками сути решения задач на движение по круговой траектории;
- Практическое освоение ими важнейших навыков в рамках транслируемого опыта;
-Активизация познавательной деятельности участников мастер-класса;
- Повышение уровня их профессиональной компетентности по основным аспектам демонстрируемой деятельности;
- Рост мотивации участников мастер-класса к формированию собственного стиля творческой педагогической деятельности.
Содержание мастер-класса
Здравствуйте уважаемые коллеги!
Я, Тюнева Надежда Васильевна, работаю в школе учителем математики .
У каждого человека в этом мире есть своё призвание. Моё - учить детей этой сложной, но интересной и увлекательной науке математике.
Говорят, что математика сухая, трудная, скучная наука. Это совсем не так! Она может быть разной: порой необычайно простой, временами сложной, но неизменно интересной увлекательной. Характер у математики непростой! Тем и интересна математика, что она такая разная и непредсказуемая. Я работаю учителем математики для того, чтобы научить каждого ученика мыслить, принимать участие в добывании знаний.
Решая интересную и сложную задачу, забываешь обо всем. И чем она труднее, тем больше радости и удовлетворения испытываешь, решив ее. Я восхищаюсь красивым решением задачи.
Моя задача – помочь ученику сделать первое и самое главное открытие в жизни – открыть свои способности к математике.
В своей педагогической работе я стараюсь использовать разнообразные приёмы, которые активизируют учебную деятельность школьников, воспитывают у них активность, самостоятельность мышления, учат применять знания в процессе обучения
Разрешите представить Вашему вниманию мастер-класс «Решение текстовых задач на движение по окружности»
Обучение школьников решению задач – одна из сложнейших методических проблем.
В настоящее время согласно Примерной основной образовательной программе основного общего образования необходимо развивать самостоятельность учащихся при решении текстовых задач на движение, которые занимают особое место при обучении математике. Математическая задача на движение, несомненно, помогает школьнику вырабатывать правильные математические понятия, в полной мере выяснить различные стороны взаимосвязей в окружающей его жизни, а также дает возможность использовать изучаемые теоретические понятия. Решение задач способствует формированию у детей полноценных знаний, определяемых программой. Через решение задач на движение учащиеся знакомятся с важными не только познавательными, но и воспитательными фактами. В теории и методике обучения математике вопросы методики обучения учащихся решению задач на движение в общеобразовательной школе рассматривали в работах Т.А. Ивановой, З.П. Матушкиной, Л.М. Фридмана, А.В. Шевкина и др.
Актуальность темы исследования обусловлена сложившимся к настоящему времени противоречием между необходимостью обучения учащихся решению задач на движение в курсе алгебры основной школы в соответствии с требованиями ФГОС основного общего образования и фактическим состоянием методики обучения их решения учащихся основной школы.
Л.М. Фридман считает, что текстовые задачи представляют собой словесные модели, в которых учащимся надо найти значения (одной или даже нескольких) неизвестной величин. Нахождение таких величин возможно потому, что оно определяется другими неизвестными и известными величинами и их взаимными соотношениями с неизвестной величиной. В задаче присутствуют для решения все данные, но бывают операции, которые должны к ним привести. Трудность выражается в 7 определении пути решения. Сложность структуры, ее индивидуальность часто может скрывать математическую сущность задач и возникает необходимость постоянно строить рассуждение, подходящее к приведенному условию . Ю.М. Колягин говорит, что текстовая задача - это описание определенной ситуации, одной или нескольких на обычном языке, где содержится требование дать количественную оценку какого-то компонента указанной ситуации или установить наличие, либо отсутствие определенного отношения между компонентами задачи, может также потребоваться определение вида данного отношения.
Решить математическую задачу – это значит найти такую последовательность общих положений математики (теорем, определений, правил, формул, аксиом, законов) которые применяя к следствиям задачи или к ее условию (результатам промежуточного решения) получаем то, что требуется к задаче – ее ответ. В каждой задаче есть условие (исходные данные), заключение - требование, которое необходимо выполнить, и субъект – это тот, кто выполняет требование.
При решении любой задачи надо выделять определенные этапы:
1 этап – это анализ условия:
проведение начального анализа текста (представление ситуации, выделение условия и требования);
выделение неизвестных, известных, искомых величин;
установление связи между данными и искомыми;
конструирование модели данной ситуации (предметные, схематические, графические) и соотношение элементов задачи с элементами модели;
установление полноты всех данных задачи (достаточность, недостаточность, избыточность); определение типа задачи.
2 этап – это планирование решения задачи:
разложение составной задачи на простые задачи;
переведение зависимости данных и искомых на тематический язык;
подбор рациональных способов решения задач;
проведение рассуждения синтетическим и аналитическим способом;
активизирование необходимых теоретические знаний для решения задачи
3 этап – это реализация найденного плана решения задачи:
установление адекватности построенной математической модели исходной задаче;
выбор математических связей между величинами;
установление соответствия промежуточного и конечного результатов;
оформление решения.
4 этап - это осуществление контроля и коррекции решения:
определение соответствия полученных результатов исходной задаче;
выполнение проверки решения разными способами;
нахождение других способов решения задачи;
оценивание полученных результатов;
обобщение результатов решения .
Л.В. Виноградова в книге «Методика преподавания математики в средней школе» отмечает, что при решении задач могут быть применены следующие методы: арифметический; геометрический; алгебраический; алгоритмический метод; эвристический, который подходит для решения нестандартной задачи.
Текстовые задачи в методической литературе разделяют по определенным основаниям на разные виды. Выбирают основание для ее проведения в зависимости от целей, классификации, затем на его основе получают определенные группы текстовых задач, которые объединяют или метод решения, или количество действий, которые надо выполнить. С целью решения задач, их можно разделить на группы по основанию:
содержанию: на проценты, на движение, на смеси и так далее;
методам решения: арифметические, алгебраические (составление уравнений, неравенство и их систем), геометрические (через использование геометрических фигур и их свойств), комбинированные;
по характеру требований: задачи на вычисление, построение, доказательство, преобразование, объяснение, конструирование;
специфике языка: текстовые (условие представлено на естественном языке), сюжетные (присутствует фабула), абстрактные (предметные).
В основу нашей классификации была положена классификация текстовых задач на движение Пасечник Л.А. и Беловой Е.И. учителей математики.. Проанализировав классификацию, которую предлагают эти учителя, следует заметить, что её можно расширить. Тем самым, считаем целесообразным, объединить эти две классификации и добавить к ней тип задач на движение по замкнутой траектории, часто встречающийся в заданиях ГИА. А так же заменить "классификацию по воде", классификацией "задачи на движение в разных средах".
С учетом выше изложенного предлагаем следующую классификацию:
1) по количеству участников движения ( задачи на движение одного человека, одного велосипедиста, одной машины и т.д; движение, в котором два и более участника);
2) по направлению движущихся объектов:( противоположно направленноедвижение: движение навстречу друг другу; движение в разные стороны; движение в одном направлении - однонаправленное движение;
3) по времени движения (по началу движения: одновременно или разновременное)
4) по характеру движения ( движение из одного пункта в другой с остановкой в пути; движение с возвратом в начальный пункт ;)
5) в зависимости от траектории движения ( прямолинейное – движение по прямой, по ровной дороге без поворотов; движение по замкнутой траектории (по стадиону, по окружности, движение автомобиля на повороте);
6) в зависимости от среды, в которой движутся объекты: ( задачи на движение по водному пути: движение по реке - по течению;- против течения ; задачи на движение по воздушному пути; задачи на движение в смешанной среде);
7) задачи на среднюю скорость,
8) задачи на движение протяженных тел.
Все методы решения задач рассчитаны на определенные знания школьников. С понятиями путь – S , скорость – V , время – t учащиеся знакомы еще с начальной школы. Так, учащимся основной школы известно, S V t (расстояние равно скорости, умноженной на время) - это формула пути. Она устанавливает зависимость между тремя основными величинами, характерными для движения любого объекта.
В основном, в задачах на движение рассматривается движение, по крайней мере, двух объектов.
Я остановлюсь на решении текстовых задач на круговое движение.
На первый взгляд кому-то задачи на круговое движение могут показаться сложными и какими-то запутанными в сравнении с обычными задачами на прямолинейное движение. Но это только на первый взгляд. Данная задача легко превращается в задачу на прямолинейное движение. Как?
1. Из одной точки круговой трассы одновременно в противоположных направлениях выехали два автомобиля. Найдите длину трассы, если автомобили встретились через 2 часа, двигаясь со скоростями 80 км/ч и 100 км/ч.
Мысленно развернем круговую трассу в прямую. На ней стоят два автомобиля, и они начинают движение навстречу друг другу. Нужно найти расстояние между ними на начало движения. Вот вам и задача на прямолинейное движение.
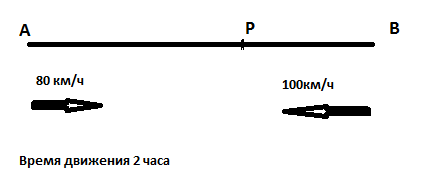
1 способ
Пусть х км – длина трассы. Тогда первый проехал 80 *2= 160 км, а второй 100*2=200км. Тогда весь путь равен х= 160+200=360 (км)
2 способ
Скорость сближения автомобилей 80+100= 180 (км\ч). Весь путь 180*2=360км
Ответ: 360 км.
2.Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 19 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 15 км/ч больше скорости другого?
1 способ.
Пусть tч – время в пути до первой встречи, тогда данные по условию задачи можно представить в виде таблицы:
|
| S , км | V, км/ч | t , ч |
| первый | xt | x (х0) | t (t0) |
| второй | (x+15)t | x+15 | t |
Составим и решим уравнение t(x+15)- tx = 9.5. x=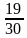 ч = 38 минут
ч = 38 минут
2 способ
В задачи взаимосвязаны три величины: путь, скорость и время. Из условия знаем, что длина пути, пройденного каждый из участников движения, равна 19:2=9,5 км( диаметрально противоположное первоначальное положение). разность скоростей равна 15 км/ч. Тогда можно найти время, за которое они пройдут этот путь, используя формулу t=ΔS/ΔV :
| ΔS= 9.5км . |
| ΔV= 15 км/ч . |
| t=Δ S :Δ V |
| 9,5:15= 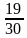 ч = 38 минут ч = 38 минут |
3 способ
Мысленно развернем круговую трассу в прямую. По ней едут два мотоциклиста, причем , один отстает от другого на 19: 2= 9,5 км(диаметрально противоположное расположение). Скорость отстающего на 15 км/ч больше скорости (он догоняет того, кто впереди). Вот вам еще одна задача на прямолинейное движение.
Итак, Искомую величину ( время, через которое они поравняются) примем за х часов. Скорость первого( находящегося впереди) обозначим у км/ч, тогда скорость второго ( догоняющего) будет (у+15) км/ч.
Занесем время и скорость в таблицу:
|
| S , км | V, км/ч | t , ч |
| первый | xу | у (у0) | х (х0) |
| второй | (у+15)х | у+15 | х |
Второй проезжает расстояние (до встречи) на 9,5 км больше, значит,
(у+15)х= xу+ 9,5;
15х = 9,5;
х= 9,5:15= 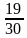 ч = 38 минут
ч = 38 минут
Ответ: 38 минут
3.Из одной точки круговой трассы длиной 30 км одновременно в одном направлении стартовали два автомобиля. Скорость первого равна 92 км/ч, скорость второго – 77 км/ч. Сколько минут пройдет с момента старта, прежде чем первый автомобиль будет опережать второго ровно на один круг?
1 способ
Решим традиционным способом с помощью таблицы:
|
| S , км | V, км/ч | t , ч |
| первый | 92t | 92 | t (t0) |
| второй | 77t | 77 | t |
| 92t - 77t = 30 15 t= 30 t= 2 часа = 120 минут |
2 способ
Мысленно развернем круговую трассу в прямую.
Из пунктов А и В, расстояние между которыми равно 30 км, одновременно выезжают два автомобиля. Скорость первого, едущего из пункта А, равна 92км/ч, а скорость второго, едущего из пункта Б, равна 77км/ч. Найдите время, за которое первый догонит второго. Вот вам еще одна задача на прямолинейное движение.
Длина пути, пройденного каждый из участников движения, равна 30 км, разность скоростей равна 92 – 77 = 15 (км/ч). Тогда можно найти время, за которое они пройдут этот путь, используя формулу t=ΔS/ΔV :
| ΔS= 30км . |
| ΔV= 15 км/ч . |
| t=Δ S :Δ V |
| 30:15 = 2 часа =120минут |
4.Из одной точки круговой трассы длиной 25 км одновременно в одном направлении стартовали два автомобиля, один из которых двигался со скоростью 112 км/ч, и через 25 минут после старта опережал второго на один круг. Найдите скорость второго автомобиля.
1 способ
За 25 мин = 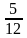 часа первый проехал 112*
часа первый проехал 112*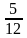 =
= 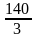 км.Второй проехал на 25 км меньше, т.е.
км.Второй проехал на 25 км меньше, т.е. 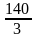 – 25=
– 25= 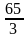 км. Этот же путь второй проехал за 25 мин, значит, его скорость
км. Этот же путь второй проехал за 25 мин, значит, его скорость 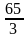 :
: 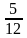 = 52 (км/ч)
= 52 (км/ч)
2 способ
Мысленно развернем круговую трассу в прямую. Задачу можно переформулировать так:
Из пунктов А и В, расстояние между которыми равно 25 км, одновременно выезжают два автомобиля. Скорость едущего из пункта А равна 112км/ч, и он через 25 минут догоняет едущего из пункта В. Найдите скорость автомобиля, выехавшего из пункта В. Вот вам еще одна задача на прямолинейное движение.
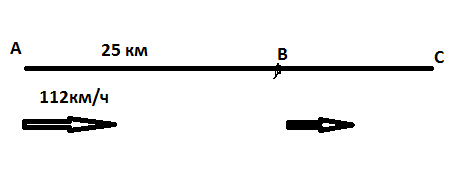
Скорость второго автомобиля можно найти:
| ΔS= 25 км . |
| t= 25 мин |
| ΔV = 25км: 25 мин= 1км/мин = 60 км/час |
Тогда скорость второго автомобиля равна 112-60= 52 (км/ч)
Ответ: 52 км/ч
5. Из пункта А круговой трассы выехал велосипедист, а через 40 минут вслед за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а через 36 минут догнал его во второй раз. Найдите скорость мотоциклиста, если длину трассы равна 30 км. Ответ дайте в км/ч.
1 способ
Пусть х км/мин – скорость мотоциклиста. За 8 минут он проехал 8х км.
Этот же путь велосипедист проехал за 48 минут. Тогда он двигался со скоростью 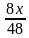 км/мин =
км/мин = 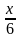 км/мин.
км/мин.
За следующие 36 минут велосипедист проехал 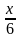 *36= 6х (км), а мотоциклист – 36х км, что на 30 км больше. Поэтому
*36= 6х (км), а мотоциклист – 36х км, что на 30 км больше. Поэтому
36х - 6х = 30; х= 1км/мин.
1км/мин= 60км/ч
2 способ
Велосипедист выехал первым и за 40 минут проехал на 30 км меньше мотоциклиста. Мотоциклист выехал позже на 8 минут. тогда за 40+8=48 минут== 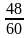 ч=
ч=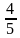 ч проехал тоже расстояние, что и мотоциклист за 8 мин=
ч проехал тоже расстояние, что и мотоциклист за 8 мин= 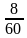 ч =
ч =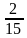 ч. Тогда скорость велосипедиста в
ч. Тогда скорость велосипедиста в 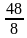 раз меньше скорости мотоциклиста.
раз меньше скорости мотоциклиста.
VМ = 6VВ . За 36 мин = 0,6 ч мотоциклист проехал на 1 круг больше, т.е. на 30 км.
0,6VМ - 0,6 VВ = 30
0,6*6VВ – 0,6 VВ = 30
3VВ = 30
VВ = 10
VМ = 6*10=60 (км/ч)
3 способ
Заполним таблицу по условию задачи:
|
| t , мин | V, км/мин | S , км |
| велосипедист | 48 | х (х0) | S |
| мотоциклист | 8 | 6х | S |
| ΔS= 30 км . |
| ΔV= 5хкм/мин. |
| Δ V = Δ S : t |
| 5х= 30км: 36 мин 5х= 30: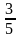 х= 10 VМ= 6*10=60км/ч. |
4 способ
Рассмотрим вторую ситуацию:
| ΔS= 30 км . |
| t= 36 мин |
| ΔV = 30км: 36 мин=5/6 км/мин = 50 км/час |
Первая ситуация:
За 48 минут велосипедист проезжает такой же путь, как мотоциклист за 10 минут. Значит, скорость мотоциклиста в 6 раз (t1:t2 = 48:8= 6 ) больше скорости велосипедиста, и разность скоростей ΔV= 5VВ.
VВ = 50: 5 = 10 (км/час) VМ= ΔV + VВ; VМ 50+10=60 (км/ч)
5 способ
Скорости участников примем за х км/ч и у км/ч. В первый раз мотоциклист обогнал велосипедиста через 8 мин = 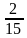 ч после старта. До этого момента велосипедист был в пути 48 мин, то есть
ч после старта. До этого момента велосипедист был в пути 48 мин, то есть 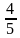 ч. Участники движения
ч. Участники движения
проехали одинаковые расстояния, то есть 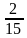 y =
y =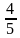 x.
x.
Внесем данные в таблицу.
| Участник движения | v (км/ч.) | t(ч) | s(км) |
| велосипедист | х | 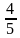
| 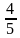 х х
|
| мотоциклист | у | 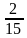
| 
|
Мотоциклист затем второй раз обогнал велосипедиста. Произошло это через 36мин, то есть через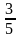 ч после первого обгона. Какие расстояния они проехали? Мотоциклист обогнал велосипедиста. А это значит, он проехал на один круг больше. Вот тот момент,на который надо обратить внимание. Один круг – это длина трассы, Она равна 30 км. Составим другую таблицу.
ч после первого обгона. Какие расстояния они проехали? Мотоциклист обогнал велосипедиста. А это значит, он проехал на один круг больше. Вот тот момент,на который надо обратить внимание. Один круг – это длина трассы, Она равна 30 км. Составим другую таблицу.
Таблица 2
| Участник движения | v(км/ч.) | t(ч) | s(км) |
| велосипедист | х | 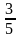
| 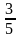 х х
|
| мотоциклист | у | 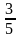
| 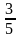 у у
|
Получим второе уравнение: 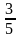 y -
y - 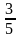 x = 30.
x = 30.
Имеем систему уравнений: 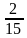 y =
y =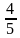 x;
x;
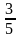 y -
y - 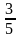 x = 30. х=10, у= 60
x = 30. х=10, у= 60
В ответе укажем скорость мотоциклиста.
Ответ: 60 км/ч
6.Из точки А круговой трассы одновременно начинают равномерное движение в противоположных направлениях два тела. Первое тело к моменту встречи проходит на 100 метров больше, чем второе, и возвращается в точку А через 9 минут после встречи. найдите длину трассы, если второе тело возвращается в точку А через 16 минут после встречи.
Мысленно развернем круговую трассу в прямую. Задачу можно переформулировать так:
Из пунктов А и В навстречу друг другу одновременно начинают двигаться два тела. Первое тело к моменту встречи проходит на 100 метров больше, чем второе, и приезжает в точку В через 9 минут после встречи. Найдите длину трассы, если второе тело прибывает точку А через 16 минут после встречи.
Пусть второе тело проходит до встречи х м, тогда первое проходит х+100 м. После встречи первое за 9 минут пройдет х м со скоростью =
= м/мин, а второе за 16 минут пройдет х+100 м со скоростью
м/мин, а второе за 16 минут пройдет х+100 м со скоростью =
=  м/мин.
м/мин.
До встречи время первогоt1= ( х+100):  мин, а второго – t2= х:
мин, а второго – t2= х:  мин. Приравняем t1=t2:
мин. Приравняем t1=t2:
( х+100):  = х:
= х:  ;
;
 =
=  .
.
7х2- 1800х -90000= 0.
х= 300 и х= -300/7.
Второе значение не подходит по смыслу задачи.
Искомое расстояние равно
300+300+100=700 (м).
Ответ: 700м
7. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 8 км до окончания первого круга, ему сообщили, что второй бегун прошел первый круг 3 минуты назад. Найдите скорость первого бегуна, если известно, что она на 9 км/час меньше скорости второго.
Обозначим скорости бегунов  и
и  . Тогда сразу можно записать их разность, которая составляет 9 км/час: Δ=
. Тогда сразу можно записать их разность, которая составляет 9 км/час: Δ=  -
-  = 9
= 9
Теперь поразмыслим над первым условием задачи. Если спустя час стало известно, что второй бегун прошел круг, значит, он прошел его за 57 минут. Обозначим длину круга S. Тогда скорость второго бегуна равна  =
= .
.
 =
=  . Подставляем эти выражения в первое уравнение. Так как в задаче присутствует неудобное число минут – 57, то представим все скорости, в том числе разность скоростей, в км/мин. Получим:
. Подставляем эти выражения в первое уравнение. Так как в задаче присутствует неудобное число минут – 57, то представим все скорости, в том числе разность скоростей, в км/мин. Получим:
 -
-  =
= 
60S-57( S-8) = 9·57
3S=57
S=19
Рассчитаем скорости обоих бегунов:
 – это 11 км/час,
– это 11 км/час,  – а это 20 км/час.
– а это 20 км/час.
Ответ: 11 км/ч
8. Два тела движутся по окружности в одну сторону. Первое проходит круг на 3 минуты быстрее второго и догоняет второе каждые полтора часа. За сколько минут первое тело проходит один круг?
Пусть длина круга равна S. Первый проходит один круг за 1 минуту, Тогда
V1= V2=
V2=  .
.
За 1,5 часа = 90 минут первое тело проходит  , второе тело проходит
, второе тело проходит  . Им
. Им =
=  + S.
+ S.
Решив получившееся уравнение ,
находим t1 = 15;t2- -18
Ответ : 15минут
Задачи для самостоятельного решения
1. Из пункта А круговой трассы выехал велосипедист, а через 30 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 30 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
2. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 6 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 9 км/ч больше скорости другого?
3. Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 89 км/ч, и через 16 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
4.Две точки равномерно вращаются по окружности. Первая совершает оборот на 5 секунд быстрее второй и делает за минуту на 2 оборота больше, чем вторая. Сколько оборотов в минуту совершает вторая точка?
5.Два гонщика стартовали одновременно из одной точки. первый через 9 кругов догоняет второго в точке старта, а еще через 0,5 часа первый обгоняет второго на 1,5 круга. Сколько кругов в час делает каждый гонщик?
6.Из одной точки круговой трассы , длина которой 12 км, одновременно в одном направлении выехали два автомобиля. Скорость первого равна 90 км/ч, и через 40 минут после старта он опережает второго на один круг. Найдите скорость второго автомобиля.
7.Из одной точки круговой трассы в разных направлениях стартовали два мотоциклиста со скоростями 55 км/ч и 45 км/ч. Через 1,5 часа они встретились во второй раз при движении по трассе. Какова протяженность трассы?
8.Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях- каждые 16 минут. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности?
Заключение
Текстовые задачи важны и необходимы :
-
для успешной сдачи ОШЭ и ЕГЭ;
-
для разрешения возникших трудностей реальной жизни;
-
для формирования умений и навыков правильного ориентирования в практической жизни;
-
для развития логического мышления и памяти;
-
для развития самостоятельной деятельности математического характера








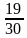 ч = 38 минут
ч = 38 минут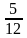 часа первый проехал 112*
часа первый проехал 112*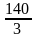 км.Второй проехал на 25 км меньше, т.е.
км.Второй проехал на 25 км меньше, т.е. 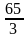 км. Этот же путь второй проехал за 25 мин, значит, его скорость
км. Этот же путь второй проехал за 25 мин, значит, его скорость 
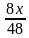 км/мин =
км/мин = 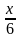 км/мин.
км/мин.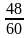 ч=
ч=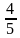 ч проехал тоже расстояние, что и мотоциклист за 8 мин=
ч проехал тоже расстояние, что и мотоциклист за 8 мин= 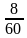 ч =
ч =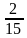 ч. Тогда скорость велосипедиста в
ч. Тогда скорость велосипедиста в 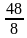 раз меньше скорости мотоциклиста.
раз меньше скорости мотоциклиста. 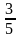








Электронная тетрадь по алгебре 9 класс...
Электронная тетрадь по алгебре 8 класс...
Математика 5 класс ФГОС
Математика. Вероятность и статистика. 7...
Электронная тетрадь по математике 6...
Геометрия 10 класс ФГОС
Математика. Вероятность и статистика. 8...
Геометрия 11 класс ФГОС
© 2021, Тюнева Надежда Васильевна 1575 28
Рекомендуем курсы ПК и ППК для учителей