Математическая игра ЧИСЛО π
Историческая справка
Число π
π (произносится «пи») — математическая константа, равная отношению длины окружности к длине её диаметра. Обозначается буквой греческого алфавита «пи». Старое название — лудольфово число.
Впервые обозначением этого числа греческой буквой 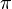 воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.
воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.
Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.
История числа 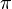 шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, в течение которого
шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, в течение которого 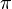 изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров.
изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров.
История числа пи начинается с древнего мира. Люди строили жилища, изобретали, исследовали окружающий мир и жили себе вполне счастливо. Сейчас трудно угадать обстоятельства (одно колесо катилось быстрее другого, совершались какие-то действия с гончарным кругом, или юный астроном пытался увидеть жителей Луны), но кому-то пришла в голову мысль об отношении длины окружности к ее диаметру.
Без всякого сомнения, это был выдающийся человек, так как именно он заметил, что это величина постоянная и не зависит от длины окружности. К сожалению, имя героя осталось неизвестным за давностью лет, так как первые упоминания об отношении длины окружности к ее диаметру и его постоянстве дошли до нас в глиняных табличках Древнего Междуречья. Именно в них мастер клинописного искусства авторитетно сообщает нам, что длина любой окружности в 3 раза больше собственного диаметра. Мы- то конечно знаем, что это не совсем верно, но люди веками пребывали в неведении до тех пор, пока за дело не взялись древние египтяне.
Математики Древнего Египта дружно начали считать, и явили миру во II тысячелетии до нашей эры новость о том, что в числе пи после целой части есть еще четыре цифры, а именно 3,1605. Следующими испытателями числа пи стали математики Древней Греции. Гиппократ с компанией единомышленников приводил измерение длины окружности к длине отрезка, который получал с помощью правильных многоугольников, построенных внутри и снаружи окружности. Архимед в 3-м веке до н.э. обобщив эти данные и увеличив количество сторон многоугольника до 96, выяснил, что числовое выражение отношения длины окружности к ее диаметру находится в промежутке между 3 10/71 и 3 1/7, т.е. пи = 3,1419.
Исследованиями числа пи занимались математики Индии и Китая, причем они весьма преуспели и уже в V веке китайский математик Цзу Чун Чжи вычислил пи как 355/113, при этом пи =3,1415927. Но, к сожалению, известным всему миру это приближение стало лишь в 1585г, и к тому же не от китайцев, а от Адриана Антониса, нидерландского математика.
XV и XVI века ознаменовались шестнадцатым знаком после запятой в результате вычисления числа пи и введением понятий рациональных и иррациональных чисел. В 1615 году было опубликован результат вычислений голландского математика Лудольфа ван Цейлен, содержащего 32 знака, поэтому выражение числа пи с 32-мя знаками после запятой стали называть числом Лудольфа. В 1706г. английский математик У.Джонсон обозначил отношение длины окружности к ее диаметру буквой пи – от начальной буквы греческих слов периферия и периметр. Но распространил этот символ для общего употребления Л.Эйлер, выдающийся математик XVIII века.
Леонард Эйлер был личностью весьма незаурядной и талантливой, значение его трудов для развития науки трудно переоценить – по книге «Основы дифференциального и интегрального исчисления» обучались математики всей Европы в течение 80 лет вплоть до 1830г. Именно Эйлер явил миру формулу связи числа пи и числа «е» (числа Эйлера).
Иррациональность числа пи была доказана окончательно в 1766г. немецким математиком Иоганном Ламбертом: число пи не может быть представлено в виде простой дроби ни в каком случае. А в конце XIX века Карл Фердинанд Линдеман также окончательно доказал трансцендентность числа пи: число пи не может быть корнем алгебраического уравнения ни в каком случае.
Этот факт явился торжественным окончанием мучений математиков всего мира с древнейших времен на протяжении 2,5 тысяч лет по поводу решения задачи о квадратуре круга. Смысл этой задачи состоял в возможности построения квадрата, равного по площади заданной окружности, используя циркуль и линейку. В благодарность освобождения от мук решения неразрешимой задачи в Мюнхенском университете перед математической аудиторией Линдеману установили бюст, а чтобы потомки не забывали причину почестей, под его именем изобразили пресекающиеся круг и квадрат, равные по площади, внутри которых мирно покоится буква пи.
Число π
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...
Стихотворения для запоминания знаков числа π
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».
Занимательные факты числа π
Существует памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле
Существует художественный фильм, названный в честь числа Пи.
Неофициальный праздник «День числа пи» ежегодно отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа 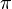 . Считается, что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159.
. Считается, что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159.
Ещё одной датой, связанной с числом 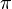 , является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа
, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа 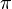 .
.
Перевести из радианной меры угла в градусную:
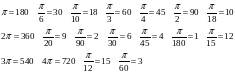
Слова, начинающиеся с ПИ:
пирамида
Соотнести название фигуры формулу для нахождения ее площади и объема:

| Название фигуры | Площадь | Объем |
| Круг | 3 | - |
| Конус | 4 | б |
| Усеченный конус | 5 | в |
| Цилиндр | 2 | а |
| Шар (сфера) | 1 | г |
Разгадайте ребусы:
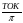 1) НАПИТОК
1) НАПИТОК
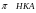 2) ЗАПИНКА
2) ЗАПИНКА
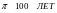 3) ПИСТОЛЕТ
3) ПИСТОЛЕТ

 4) ПИРОГ
4) ПИРОГ
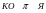 5) КОПИЯ
5) КОПИЯ

 Б=М 6) ПИЖАМА
Б=М 6) ПИЖАМА
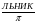 7) НАПИЛЬНИК
7) НАПИЛЬНИК
 а) ПИОН
а) ПИОН

 а б) ПИЛА
а б) ПИЛА
 в) ПИАНИНО
в) ПИАНИНО
 г) ПИДЖАК
г) ПИДЖАК

 О=А д) ПИРАТ
О=А д) ПИРАТ
 е) СПИРТ
е) СПИРТ
ж) ПИОНЕРБОЛ
Назовите по памяти число ПИ
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...
| Название фигуры | Площадь | Объем |
| Круг |
|
|
| Конус |
|
|
| Усеченный конус |
|
|
| Цилиндр |
|
|
| Шар (сфера) |
|
|
| Название фигуры | Площадь | Объем |
| Круг |
|
|
| Конус |
|
|
| Усеченный конус |
|
|
| Цилиндр |
|
|
| Шар (сфера) |
|
|



























































































| 1 | А |
| 2 | Б |
| 3 | В |
| 4 | Г |
| 5 | Д |
| 6 | Е |
| 7 | Ж |
| 1 | А |
| 2 | Б |
| 3 | В |
| 4 | Г |
| 5 | Д |
| 6 | Е |
| 7 | Ж |
Б=М
а


О=А







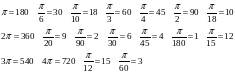

 1) НАПИТОК
1) НАПИТОК 2) ЗАПИНКА
2) ЗАПИНКА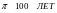 3) ПИСТОЛЕТ
3) ПИСТОЛЕТ
 4) ПИРОГ
4) ПИРОГ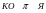 5) КОПИЯ
5) КОПИЯ Б=М 6) ПИЖАМА
Б=М 6) ПИЖАМА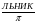 7) НАПИЛЬНИК
7) НАПИЛЬНИК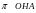 а) ПИОН
а) ПИОН а б) ПИЛА
а б) ПИЛА в) ПИАНИНО
в) ПИАНИНО г) ПИДЖАК
г) ПИДЖАК О=А д) ПИРАТ
О=А д) ПИРАТ е) СПИРТ
е) СПИРТ









