Математические и статистические функции.

Группа С-11, 2025 года

Занятие по рабочей программе №09

Дисциплина: ОП.03 «Информационные технологии в профессиональной деятельности»

Раздел 3. Технология обработки числовой информации.

Тема: Математические и статистические функции.

1. Цель занятия:

   1. Дидактическая:

• сформулировать представление студентов о понятии Технология обработки информации;

• выяснить основные понятия MS EXCEL;

• раскрыть способы ввода, перемещения и копирование формул в таблицу;

• выяснить принципы и методы использования Финансовых функций;

• систематизировать и обобщить знания по работе с Функциями даты и времени;

• углубить и закрепить знания по дисциплине «Информационные технологии в профессиональной деятельности».

Воспитательная:

• развивать коммуникативные способности;

• развивать аналитические способности;

• развивать творческий подход к процессу обучения.

• воспитывать самостоятельность, дисциплинированность;

• стимулировать студентов к изучению дисциплины;

• побуждать к формированию активной жизненной позиции;

• прививать уважение и любовь к будущей профессии.

Вид занятия: лекция.

Тип занятия: обобщение и систематизация знаний.

Форма проведения занятия: репродуктивная и эвристическая беседа.

Междисциплинарные связи:

Обеспечивающие ОГСЭ.04 Физическая культура, МДК.04.01 Основы управления работами спец. подразделения швейного производства.

Обеспечиваемые ОП.01 Инженерная графика, ОП.08 Общая технология отрасли, ОП.11 Экономика, организация и планирование производства, ОП.16 Маркетинг в отрасли.

Методическое обеспечение: опорный конспект.

Литература:

1. Михеева, Е.В. Практикум по информационным технологиям в профессиональной деятельности : учебное пособие. - М. : Академия, 2008. - 8 – е изд. - 256 с.- (Среднее профессиональное образование), стр. 179 – 188

2. Практикум по MS Excel - http://informatika.delayu.ru/Zadanija/Exceldannye

ХОД ЗАНЯТИЯ

1. Ознакомление с темой, целью и планом занятия.

Тема: Математические и статистические функции.

ПЛАН

1. Общие сведения о функциях.

2. Математические и статистические функции.

3. Финансовые функции.

1. Изложение и изучение нового материала.

ЛИТЕРАТУРА: [2], стр. 179 - 188

1. Общие сведения о функциях

В любом табличном процессоре используются встроенные функции.

Встроенная функция — это заранее написанная процедура преобразования данных.

Всё многообразие встроенных в табличные процессоры функций принято делить на категории по их назначению, выделяя среди них математические, статистические, логические, текстовые, финансовые и другие типы функций.

Каждая встроенная функция имеет имя — как правило, это сокращённое название производимого ею действия. Функции вызываются с некоторыми аргументами и возвращают единственное значение — результат обработки.

Аргументом функции может быть число, текст, выражение, ссылка на ячейку или диапазон ячеек, результат другой функции. Можно выделить функции:

• с одним аргументом, например КОРЕНЬ;

• с несколькими аргументами, количество которых фиксировано, например ОКРУГЛ;

• с нефиксированным количеством аргументов, например МАКС;

• с некоторыми необязательными аргументами, например РАНГ;

• без аргументов, например ТДАТА.

При использовании функции в формуле сначала указывается её имя, а затем в скобках указывается список аргументов через точку с запятой (табл. 1.).

Таблица 1

Примеры записи функций

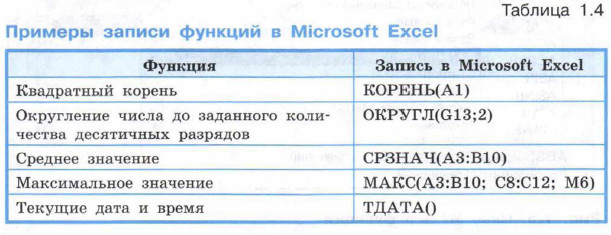
Назначение каждой функции, наличие аргументов, их количество и тип можно посмотреть в Справке или в комментариях при вводе функции в формулу.

Вставить функцию в формулу можно несколькими способами:

1) использовать кнопки категорий функций в группе Библиотека функций вкладки Формулы на ленте;

2) воспользоваться инструментом Вставить функцию в группе Библиотека функций или в строке формул;

3) ввести функцию непосредственно в ячейку или в поле Строка формул.

Рассмотрим более подробно второй способ.

Если щёлкнуть на кнопке Вставить функцию строки формул, то откроется окно Мастер функций (рис. 1.), а в текущую ячейку автоматически вставится знак «=» (если в этой ячейке ввод формулы ещё не начинался). В окне Мастер функций в списке поля Категория можно выбрать нужную категорию, после чего в списке поля Выберите функцию выбрать нужную функцию.

Рис.1. Окно Мастер функций

2. Математические и статистические функции

Для решения математических задач (решения уравнений, построения графиков функций) вам могут быть полезны функции, представленные в таблице 2. Здесь же представлены некоторые из статистических функций, позволяющих автоматизировать статистическую обработку данных. С их помощью можно вычислить наименьшее значение, подсчитать количество ячеек, содержащих заданную информацию, и т. д.

Рассмотрим более детально работу статистической функции РАНГ, имеющую формат:

РАНГ(число; ссылка на список; [порядок])

Здесь:

• число — это число, для которого определяется ранг (порядок);

• ссылка на список — ссылка на список, которому принадлежит число (нечисловые значения в ссылке игнорируются);

• порядок — способ упорядочения значений списка:

• О или отсутствие параметра - определяет ранг (позицию, место) числа в списке так, как если бы список был отсортирован в порядке убывания (т. е. максимальному значению присваивается ранг равный 1, чуть меньшему числу - ранг 2 и т. д.);

• число, не равное 0, - определяет ранг числа так, как если бы список сортировался в порядке возрастания (т. е. минимальному числу присваивается ранг 1, чуть большему числу - ранг 2 и т. д.).

Таблица 2

Некоторые Математические и статистические функции

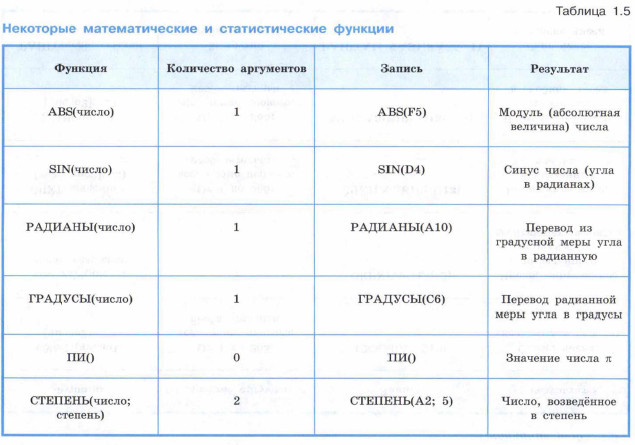
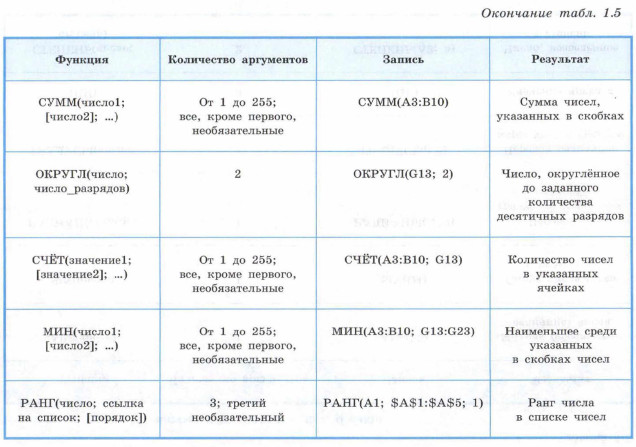
Функция РАНГ присваивает повторяющимся числам одинаковый ранг. При этом наличие повторяющихся чисел влияет на ранг последующих чисел.

 В ячейку В1 введена и скопирована в В2:В6 одна из двух следующих формул:

1) =РАНГ(А1; $А$1 :$А$6; 1);

2) =РАНГ(А1; $А$1 :$А$6; 0).

По какой из формул представлены результаты вычислений в столбце В?

Как вы можете объяснить отсутствие числа 2 среди значений ячеек диапазона С1:С6, если это — результаты вычислений по другой из приведённых выше формул?

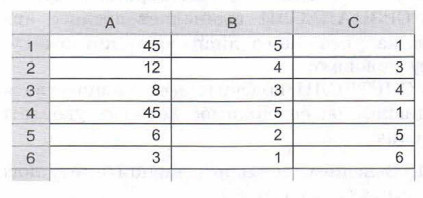
Рис. 2. Таблица

3. Финансовые функции

Финансовые функции используются для вычисления размеров выплат при погашении кредитов, банковских процентов на вклады, для определения процентной ставки и др.

Рассмотрим несколько финансовых функций, которыми полезно уметь пользоваться каждому человеку, планирующему взять в банке кредит¹ или сделать вклад². Аргументами этих функций являются:

Кредит — это ссуда, предоставленная кредитором (в данном случае банком) заёмщику под определённые проценты за пользование деньгами.

Вклад — денежные средства, внесённые физическим или юридическим лицом в финансовое учреждение на хранение, в рост или для участия в получении прибыли.

• ставка — процентная ставка за период;

• плт — выплата, производимая в каждый период (месяц, квартал, год и т. п.);

• пс — приведённая (нынешняя) стоимость инвестиции;

• кпер — общее число периодов платежей по кредиту;

• бс — будущая стоимость инвестиции;

• тип — число 0, если оплата в конце периода; число 1, если оплата в начале периода (по умолчанию — 0).

Пример 1. Пусть ставка кредита в некотором банке составляет 18% годовых. Клиент хочет взять кредит на сумму 100 000 руб. и может выплачивать банку по 4000 руб. ежемесячно. Нужно определить, за сколько периодов клиент сможет погасить этот кредит.

Функция КПЕР(ставка; плт; пс; [бс]; [тип]) возвращает количество периодов платежей для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки. Обязательные аргументы функции:

• ставка — годовая ставка в процентах, разделённая на количество периодов платежей за год (в нашем примере это 18%/12);

• плт — сумма, которую клиент ежемесячно должен возвращать банку (в нашем примере это -4000, т. к. эти деньги отдаются);

• пс — размер кредита (в нашем примере это 100 000).

Формула для вычисления количества периодов выплат для погашения взятого кредита будет иметь вид:

=КПЕР(18% /12; -4000; 100000).

Получаем приблизительно 32 периода (месяца), т. е. более 2,5 лет.

Пример 2. Выясним, на какую сумму клиент может взять кредит, если ставка 19% годовых, а выплачивать он может по 12 000 руб. на протяжении двух лет (24 периода).

Функция ПС(ставка; кпер; плт; [бс]; [тип]) возвращает приведённую (к текущему моменту) стоимость инвестиции, представляющую собой общую сумму, которая на данный момент равноценна ряду будущих выплат.

Обязательные аргументы функции:

• ставка (19%/12);

• кпер — общее количество периодов выплаты платежей по кредиту (24);

• плт (-12 000).

Формула для вычисления размера кредита будет иметь вид:

=ПС(19%/12; 24; -12000).

Получаем приблизительно 238 054 руб.

Пример 3. Пусть клиент хочет взять кредит 100 000 руб. на 2 года. При этом выплачивать он может по 5000 руб. ежемесячно. Может ли он воспользоваться предложением банка, ставка по кредитам в котором составляет 20% ?

Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) вычисляет процентную ставку за период (а не за год).

Обязательные аргументы функции:

• кпер (24);

• плт (-5000);

• пс (100 000).

Формула для вычисления ставки будет иметь вид:

=СТАВКА(24; -5000; 100000).

В результате вычислений получаем процентную ставку за месяц 1,51308%. Соответственно, процентная ставка за год составит 18,157% (1,51308 • 12). Таким образом, клиенту не рекомендуется брать кредит в банке, ставка по кредитам в котором составляет 20%.

Пример 4. Клиент хочет сделать вклад на 3 года на сумму 300 000 руб. под 11% годовых с ежемесячным начислением процентов. Выясним, какую сумму он получит по окончании срока вклада.

Функция БС(ставка; кпер; плт; [пс]; [тип]) возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки. Иначе говоря, с её помощью можно вычислить сумму, которую выплатят клиенту за вклад под определённые проценты по окончании срока вклада. Аргументы функции:

• ставка — годовая ставка в процентах, разделённая на количество периодов начисления процентов за год (в нашем примере это 11%/12);

• кпер — количество периодов начисления процентов (3 • 12 = 36);

• плт — сумма, которая добавляется к вкладу каждый период времени: 0 или отрицательное число (в нашем примере это 0, т. к. пополнение вклада клиентом не предусмотрено);

• пс — начальная сумма вклада (в нашем примере это 300 000).

Формула для вычисления суммы, которую клиент получит за вклад по окончании срока вклада, будет иметь вид:

=БС(11% /12; 36; 0; -300000).

В результате вычислений получаем 416 663,58 руб.

Пример 6. Клиент хочет сделать вклад на 2 года на сумму 100 000 руб. под 10,5% годовых с ежемесячным начислением процентов. При этом он имеет возможность ежемесячно пополнять вклад ещё на 2000 рублей. Выясним, какую сумму клиент получит по окончании срока вклада.

Для нахождения результата мы воспользуемся той же функцией, что и в примере 5. Отличие состоит в том, что аргумент плт в этом случае примет значение -2000.

Формула для вычисления суммы, которую клиент получит за вклад по окончании срока вклада, будет иметь вид:

=БС(10,5%/12; 24; -2000; -100000).

В результате вычислений получаем 176 409,84 руб.

Как изменится формула в примере 6, если клиент ежемесячно будет не пополнять счёт на 2000 руб., а снимать со счёта по 1000 руб.?

Контрольные вопросы

1. Что такое функция? Что такое Мастер функций и какие способы его запуска вы знаете?

2. Как следует записывать аргумент тригонометрической функции, если он записан в градусах?

3. При делении на нуль программа выдает сообщение об ошибке. Какой функцией можно воспользоваться, чтобы исключить появление такого сообщения? Запишите пример формулы.

4. Как установить (изменить) точность отображения числа и результата вычислений?

5. Опишите назначение и порядок выполнения сортировки списков.

6. Как с помощью автозаполнения ввести в ячейки B19 – G19 числа начиная с 0 и кратные 2?

7. Что является главной особенностью при вводе формул?

8. Какую функцию в формуле выполняют круглые скобки?

9. Как получить сумму диапазона ячеек?

10. Как можно отредактировать содержимое ячейки?

11. Какие функции относятся к статистическим?

12. Какие функции относятся к математическим?

13. Как записать математическую функцию в Excel?

ДОМАШНЕЕ ЗАДАНИЕ

1. Составить конспект лекции.

2. Ответить письменно на контрольные вопросы.

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.

Основные источники:

1. Гохберг, Г.С. Информационные технологии: учебник для студ. сред. проф. Образования / Гохберг, Г.С, Зафиевский, А.В., Короткин, А.А. – 5 - е изд., стер. – М .: Издательский центр «Академия», 2010. – 208с.

2. Михеева, Е.В. Практикум по информационным технологиям в профессиональной деятельности : учебное пособие. - М. : Академия, 2008. - 8 – е изд. - 256 с.- (Среднее профессиональное образование).

3. Филимонова, Е.В. Информационные технологии в профессиональной деятельности : учебник. – Изд - е 2 - е, доп. и перераб. – Ростов н / Д : Феникс, 2008. – 381. – (СПО).

Интернет - источники:

1. Электронный учебник по информатике и информационным технологиям - http://www.ctc.msiu.ru/

2. Тесты по информатике - http://www.ege.ru/

3. Каталог образовательных Интернет-ресурсов: учебно-методические пособия - www.edu/ru/modules.php

4. Дидактические материалы по информатике - http://comp-science.narod.ru/

5. Портал электронного обучения - http://www.e-learning.by/

6. Электоронный учебник «Работа с MS Excel» - http://avanta.vvsu.ru/met_supply/381/Index.htm

7. Практикум по MS Excel - http://informatika.delayu.ru/Zadanija/Exceldannye

Преподаватель: Владимир Александрович Волков