Математические методы в химии и биологии

Введение.

Математика – царица всех наук. Как часто мы слышим эти слова, сказанные немецким математиком Карлом Гауссом (1777-1855) много лет назад. Эти слова можно подтвердить и высказываниями других ученых. Александров А.Д. говорил: «Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения. Сейчас уже нельзя назвать такой области деятельности людей, где математика не играла бы существенной роли. Она стала незаменимым орудием во всех науках о природе, в технике, в обществоведении. Даже юристы и историки берут на своё вооружение математические методы» Слова Гнеденко Б.В, советского математика, подтверждают это высказывание: «В нашу современную жизнь вторгается математика с ее особым стилем мышления, становящимся сейчас обязательным и для инженера, и для биолога»

Очень часто задачи, решаемые математическими способами, включаются в олимпиадные задания и обязательно - в ЕГЭ по химии и биологии, не так давно они также появились в заданиях ЕГЭ по математике, где можно решить задачу любым способом, потому что требуется записать только ответ.

Существуют различные методы решения химических задач. На начальном этапе обучения химии используется главным образом логически-словесный способ (метод пропорций). Такой способ требует значительного времени для подготовки ответа, так как включает в себя промежуточные расчёты и поэтому он неудобен при тестировании и сдаче экзаменов.

Каким образом математика применяется в изучении химических и биологических явлений? Чтобы ответить на этот вопрос, были поставлены следующие цели и задачи:

1. Показать возможность применения математических методов в биологии и химии.

2. Познакомиться с формулами, описывающими реальные процессы в жизни, и научится решать задачи по этим формулам.

3. Найти наиболее рациональные математические методы решения химических и биологических задач.

1. Математика и химия.

В настоящее время, математика широко применяется в разных областях знаний, в том числе в химии. Существует даже такое понятие, как математическая химия. Возникает вопрос о изучении и исследовании математических методов и их возможности для применения в химической науке. Понятие «процента» вошло в нашу жизнь не только с уроками в средней школе и с проведением сложных научно-исследовательских работ, но и с выпечкой кулинарных изделий и приготовлением лакомств, солений и варений. Эта работа поможет систематизировать знания и умения по теме проценты, повысить свою математическую и алгоритмическую культуру, достичь уверенных навыков в решении стандартных задач по алгебре, освоить эвристические подходы к решению творческих задач, а также сформировать привычку поисковой активности, существенную отнюдь не только при занятиях математикой, но и в обыденной жизни.

Эта работа для тех, кто изучает математику, химию, кому завтра предстоят экзамены выпускные, кому в повседневной жизни приходится производить расчеты на определение концентрации раствора.

Химия сродни не только искусству, но и волшебству. Многие химические опыты, сопровождающиеся неожиданным изменением цвета, объема или агрегатного состояния, производят на непосвященных людей магическое впечатление. Химикам присущ уникальный, характерный только для них, взгляд на окружающий мир. Химики должны проявлять такие характеристики креативной личности, как быстрота, точность, оригинальность мышления, богатое воображение, самообладание, мобильность, инновационность и уверенность в себе. Креативный химик всегда «чувствует вещество». Это проявляется и в лаборатории, где создаются рецепты синтеза новых веществ, и в быту, где, например, бывает нужно подобрать подходящий клей или растворитель. Современные креативные химики при изучении химических процессов используют законы математики.

Для описания веществ и реакций используют теории, в которых роль математики настолько велика, что иногда трудно понять, где химия, а где математика. Отсюда следует, что и химия немыслима без математики.

Математика для химиков – это, в первую очередь, полезный инструмент решения многих химических задач. Очень трудно найти какой-либо раздел математики, который совсем не используется в химии. Функциональный анализ и теория групп широко применяются в квантовой химии, теория вероятностей составляет основу статистической термодинамики, теория графов используется в органической химии для предсказания свойств сложных органических молекул, дифференциальные уравнения – основной инструмент химической кинетики, методы топологии и дифференциальной геометрии применяются в химической термодинамике. Выражение «математическая химия» прочно вошло в лексикон химиков. Многие статьи в серьезных химических журналах не содержат ни одной химической формулы, зато изобилуют математическими уравнениями.

При решении химических задач часто возникает потребность проводить вычисления для нахождения соотношений составных частей в различных объектах. В качестве последних можно рассматривать химические соединения, смеси веществ, сплавы.

В задачах обычно рассматриваются объекты, которые состоят из компонентов. Количественный состав объектов удобно выражать в долях, которые составляют компоненты по отношению к целому объекту. Употребляют массовую, объемную и молярную доли. Массовая доля w (X) i-го компонента, входящего в состав объекта, равна отношению массы этого компонента m (X) к массе объекта m (об) и выражается в долях единицы или в процентах.

Массу компонента в объекте вычисляют, умножив массу объекта на массовую долю компонента в нем: m(x) = m (об) • w(x)

Так, зная химический состав соединений, т. е. их формулы и молярные массы, можно вычислять массовые доли элементов в этих соединениях. И наоборот, зная массовые доли элементов в соединениях, можно находить молекулярную формулу соединения.

Ниже приведены примеры решения отдельных задач. Все они принадлежат к одному типу, поэтому алгоритмы их решения идентичны. В преобладающем большинстве случаев ход решения строится так: обозначаем буквами неизвестные величины и формулируем их физический смысл; словесно формулируем смысл уравнений и неравенств, которые затем записываем с помощью символов; подставляем числовые значения; решаем систему уравнений и неравенств и даем ответ.

Приведем примеры решения задач.

Задача №1.

В сосуд, содержащий литров - процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение: В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

Задача № 2.

К 60 г. соли добавили 100 г. воды. Определите содержание соли в растворе в %.

Решение:

- найдем массу всего раствора: 60+100=160 (г)

- отсюда находим содержание соли в %: 150 г. -100%

60 г. – х

х=60*100/150=40%

Ответ: в растворе 40% соли.

Задача № 3

Массовая доля кислорода в одноосновной аминокислоте равна 42,67%. Установите молекулярную формулу кислоты.

Решение:

Рассчитать молярную массу кислоты CnН2n (NН₂) CОOH

w (О) = M кислоты=75 (г/моль) 

Найти число атомов углерода в молекуле кислоты и установить её формулу

М = 12 n + 2 n + 16 + 45 =75

14 n = 14, n = 1

Ответ: формула кислоты NН₂CН₂CОOH

М (NН₂CН₂CОOH) = 75 г/моль

3. Математика и биология.

Биология широко использует математический аппарат при проведении тех или иных исследований. Любое исследование предполагает статистическую обработку результатов: ранжирование, построение графиков и диаграмм, подсчёт среднего арифметического, среднеквадратичного отклонения, процентной доли, коэффициентов корреляции. При изучении генетических законов, решении задач по генетике, биохимии и популяционной генетике математический аппарат необходим как при освоении теоретического материала, так и при решении конкретных задач.

З олотое сечение в природе. На уроках ботаники мы обращаем внимание на то, что очередное листорасположение подчиняется правилу золотого сечения: дробь, числитель которой — это число оборотов на стебле, а знаменатель — число листьев в цикле, соответствует рядам Фибоначчи, например, 3/8 или 5/13. Логарифмическую спираль можно обнаружить в расположении семян корзинках сложноцветных, чешуй — в шишках голосеменных, колючек на стебле кактусов.

Во всех этих случаях спирали заворачиваются навстречу друг другу, а число правых и левых спиралей всегда относится друг к другу как соседние числа в ряду Фибоначчи.

В биологии так же широко используется показательная функция. Рост различных видов микроорганизмов и бактерий, дрожжей и ферментов подчиняются одному закону: N=N₀e^kt. По этому закону возрастает количество клеток гемоглобина в организме человека, который потерял много крови.

Рассмотрим такие задачи:

1) Численность популяции составляет 5 тыс. особей. За последнее время в силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида?

Решение: Применим для вычисления времени формулу сложных процентов: 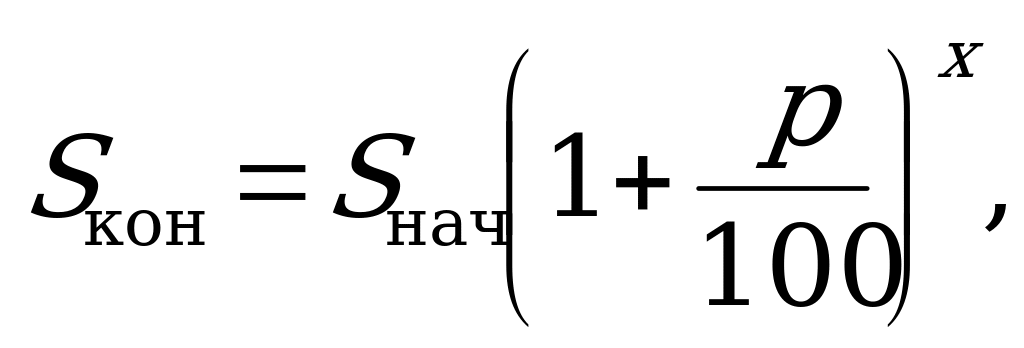где

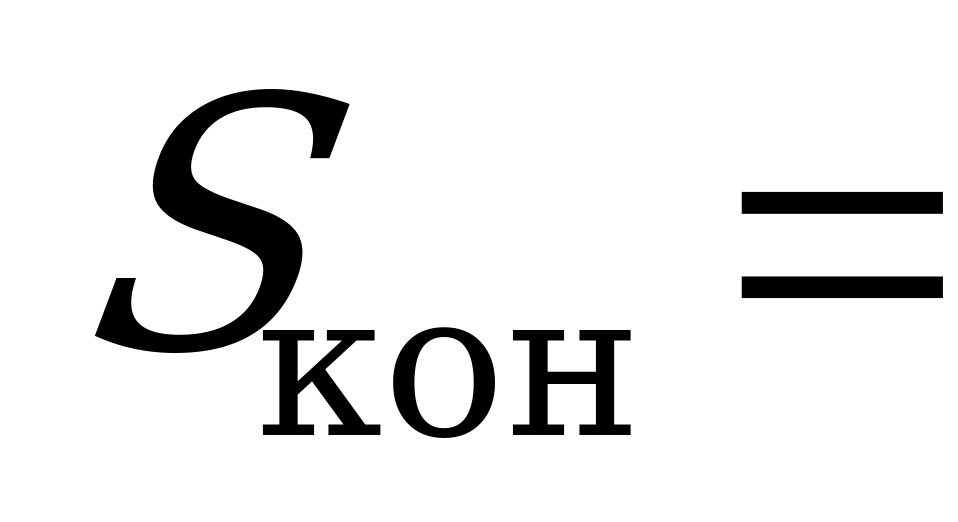2 тыс. – численность животных по истечению искомого времени;

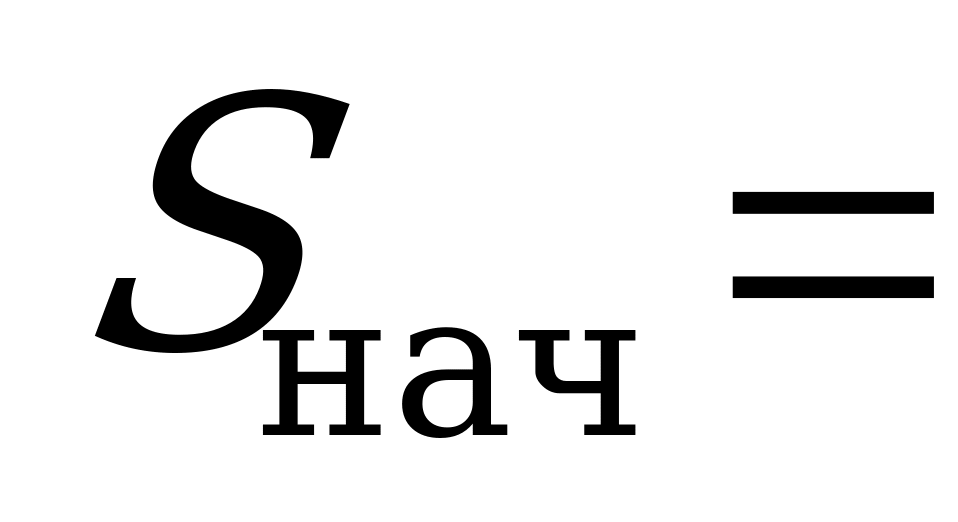5 тыс. – численность животных в начальный момент времени;

p = 8 - % сокращения численности животных.

Предварительно разделив обе части уравнения на 1000, получим:

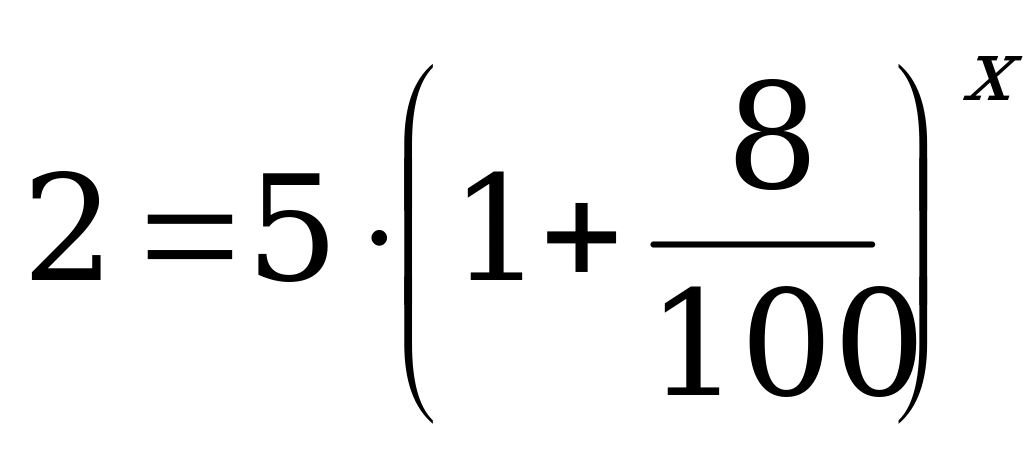
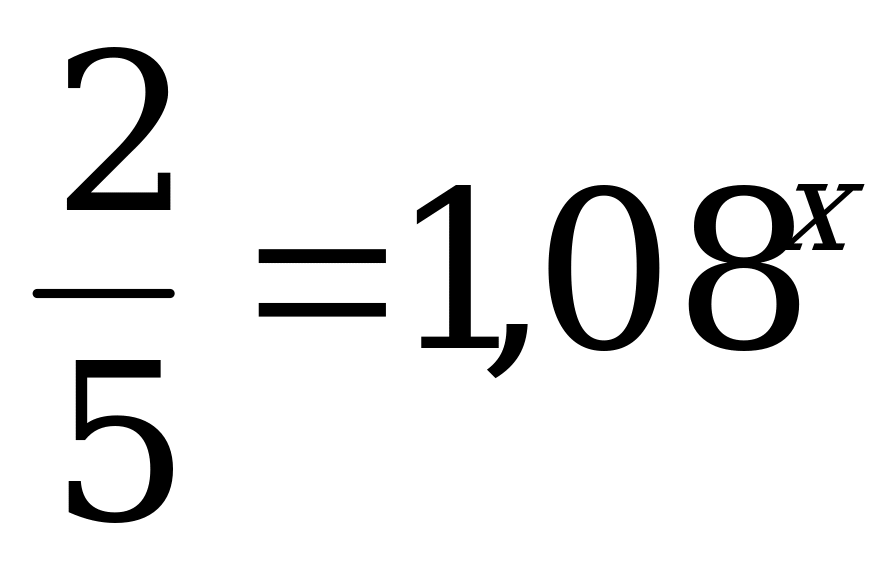
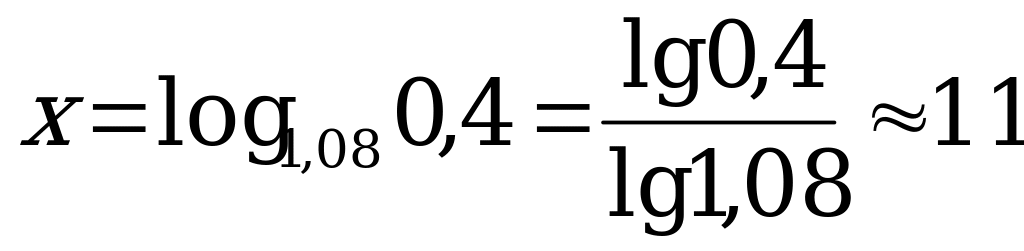лет.

Ответ: Приблизительно через 11 лет.

2) Рассмотрим задачу об органическом росте в общем виде.

Пусть в начальный момент времени имелось q единиц некоторого компонента. В некоторый другой момент времени t имеющийся компонент изменился в p раз. Установите, через какой промежуток времени (начиная с начального момента) этот компонент достигнет заданного количества B единиц.

Решение: Для того чтобы это сделать, сначала напомним, что процессы, у которых происходит быстрый рост или быстрое затухание, описываются показательной функцией вида .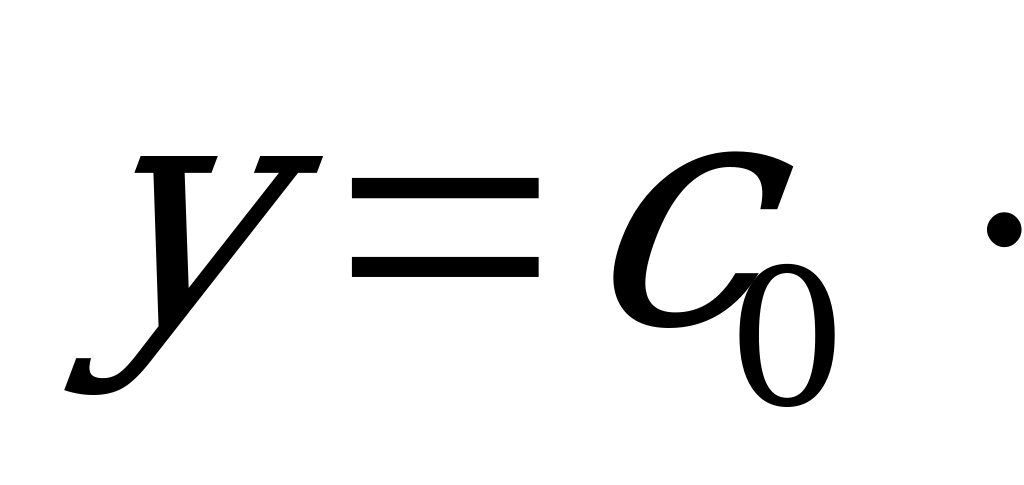

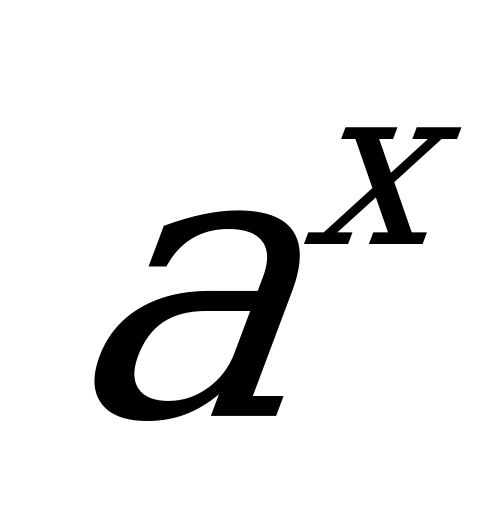В нашем случае будем считать, что начальный момент времени соответствует нулю, тогда 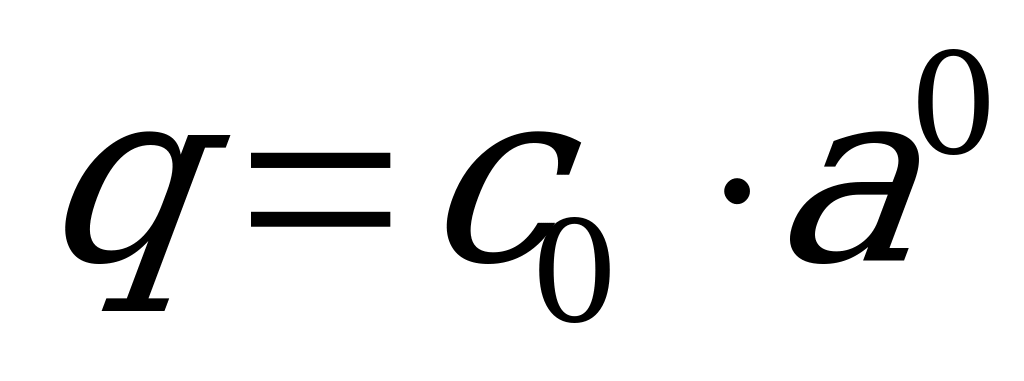, и значит, 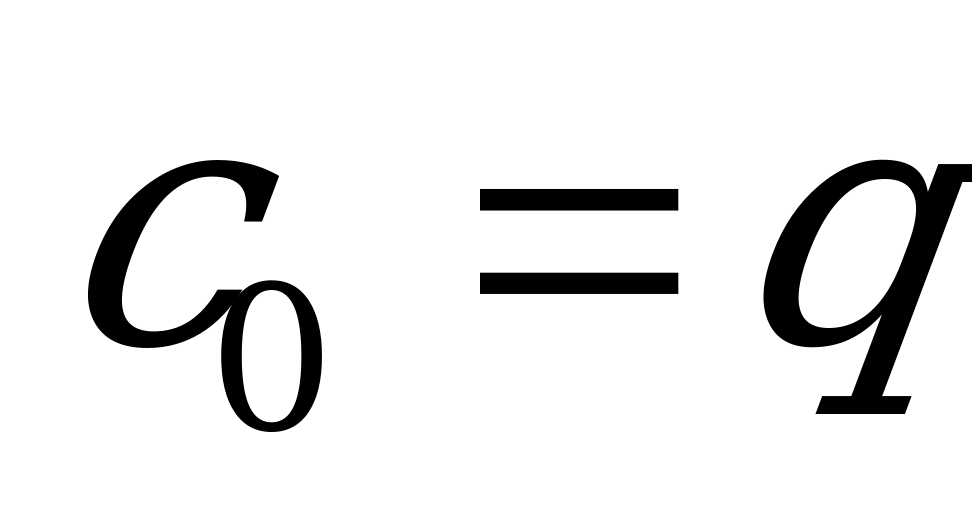, т.е. функция, описывающая этот процесс, имеет вид 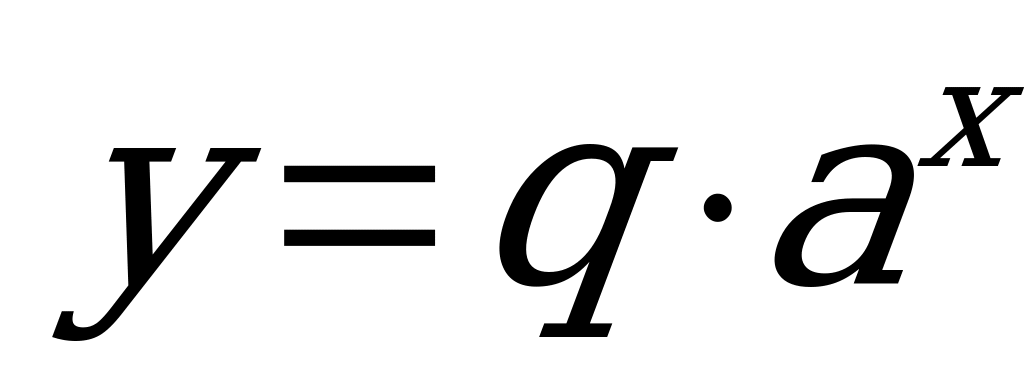. В следующий момент времени t у нас произошли изменения, описываемые уравнением 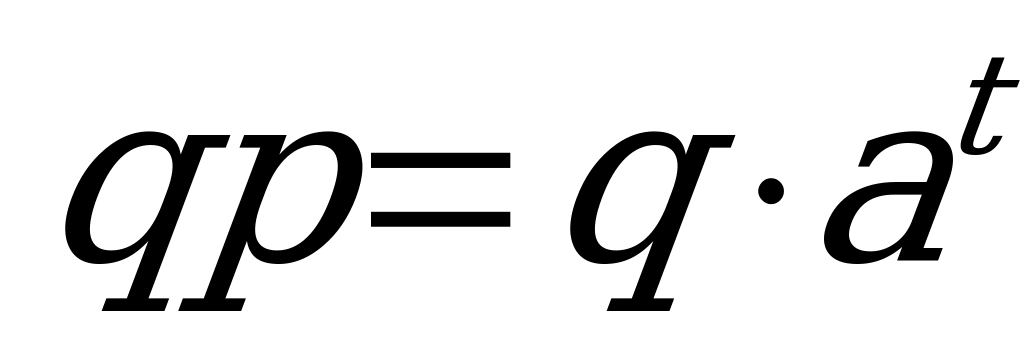, т.е. 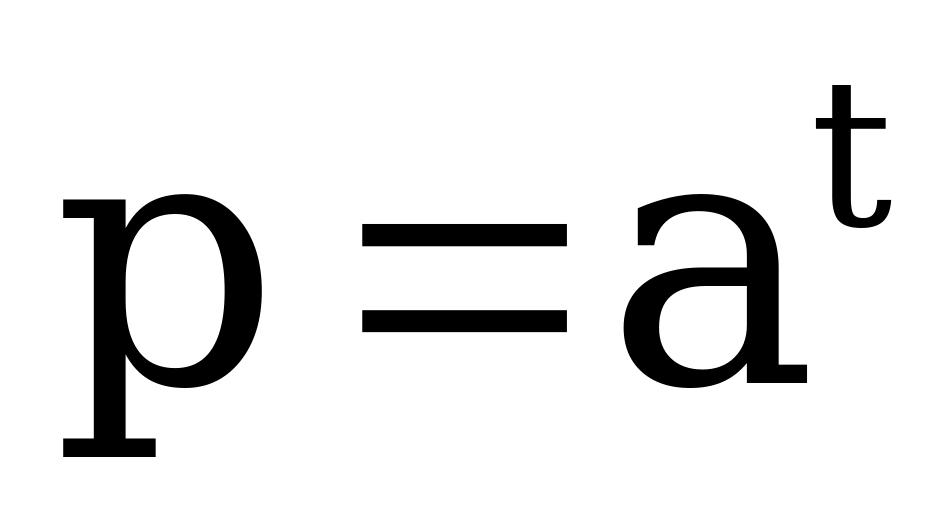, откуда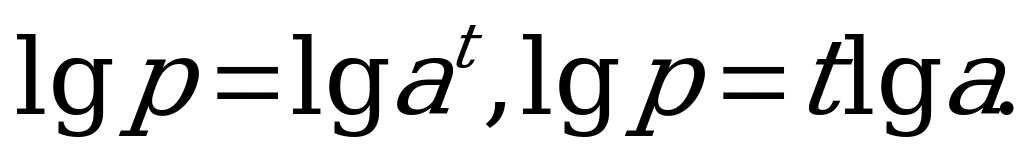

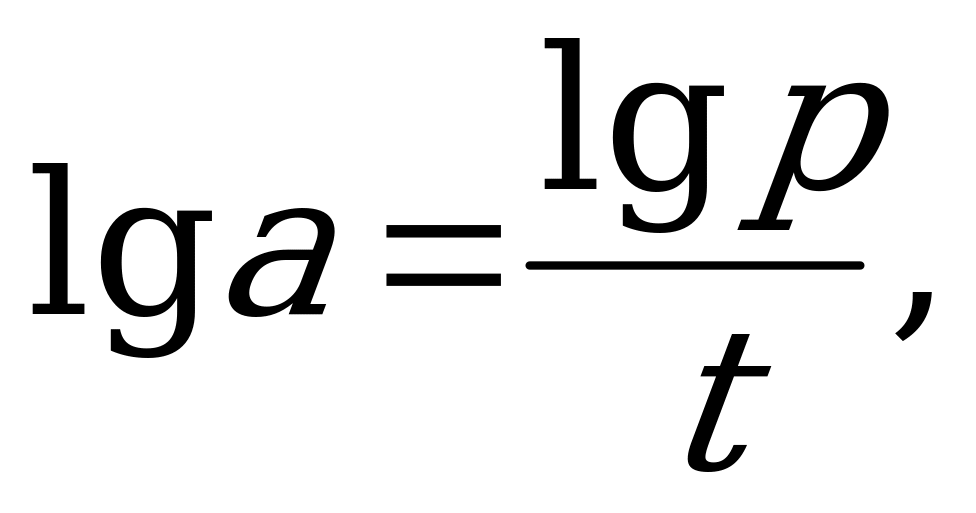
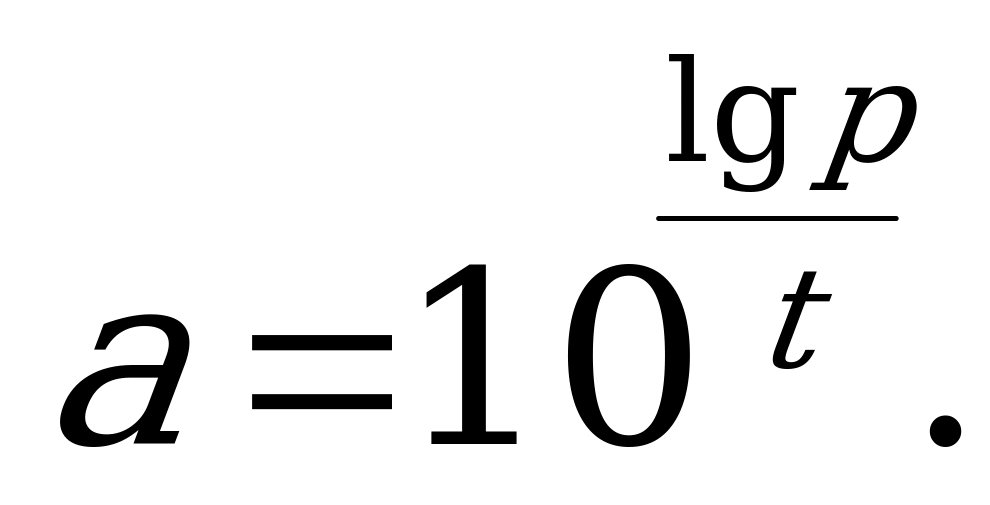Таким образом, по данным условия мы получаем функцию 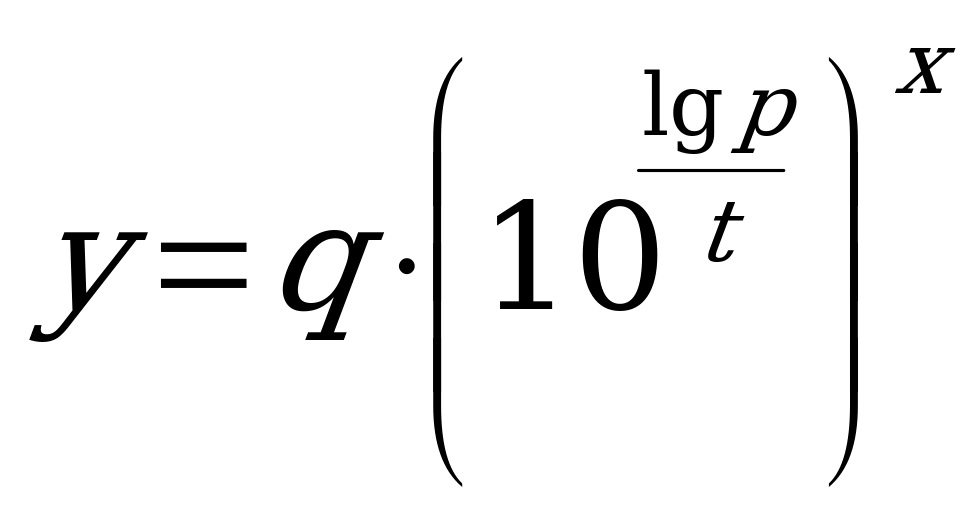. И теперь ясно, что мы ищем x, при котором 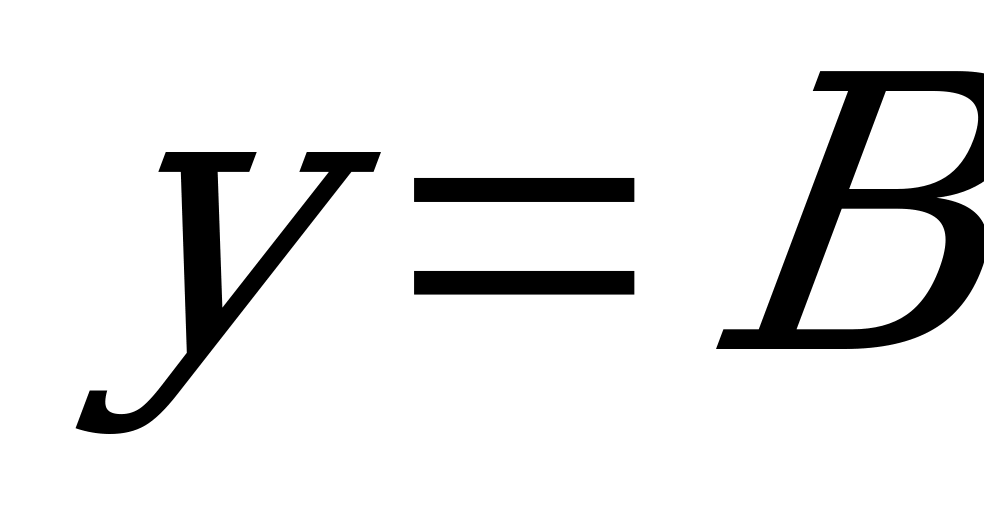, т.е. надо решить уравнение 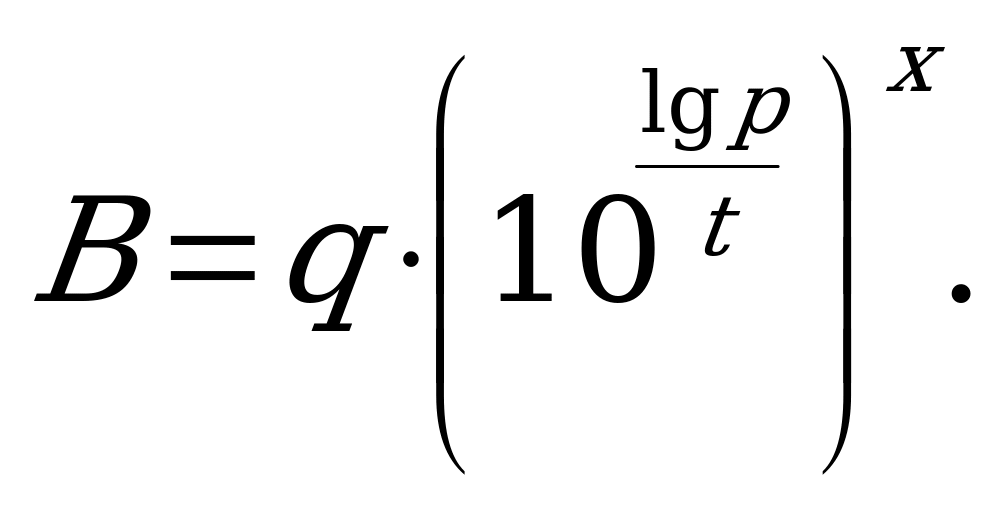Выполняя логарифмирование уравнения 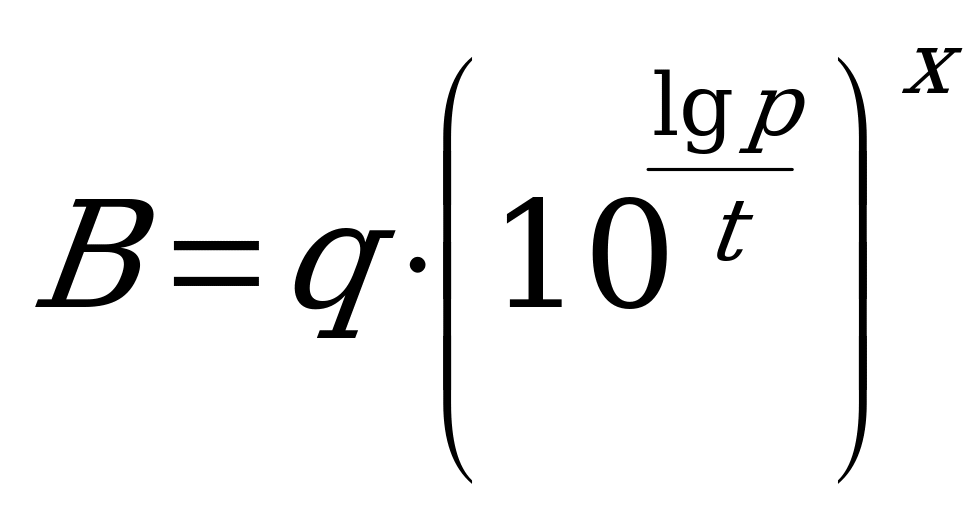по основанию 10, получим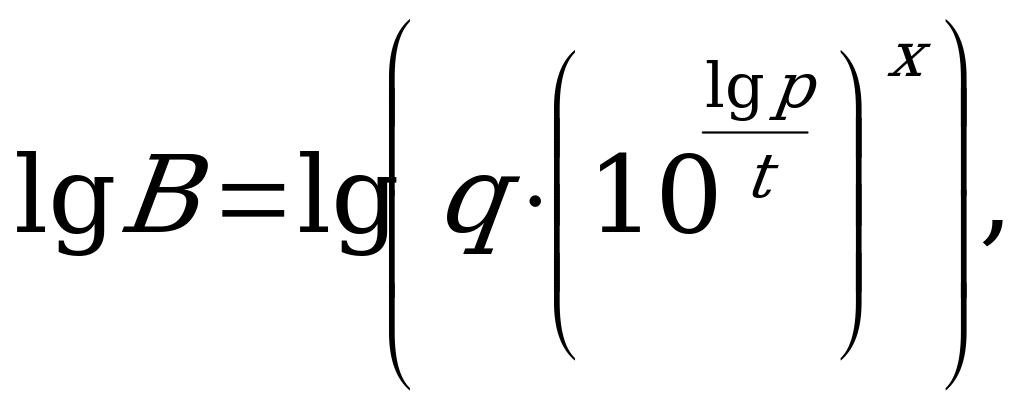

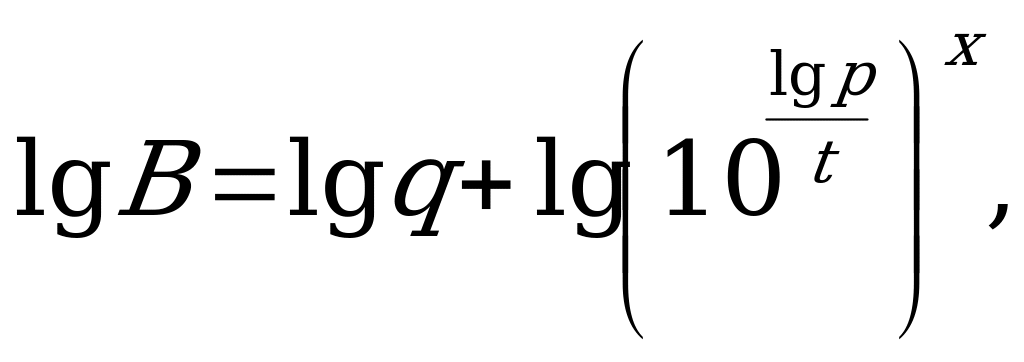
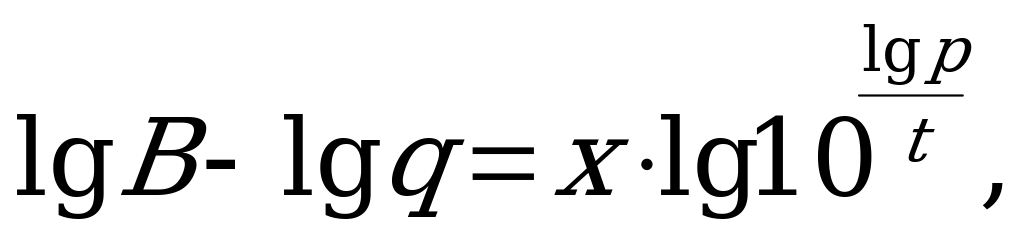
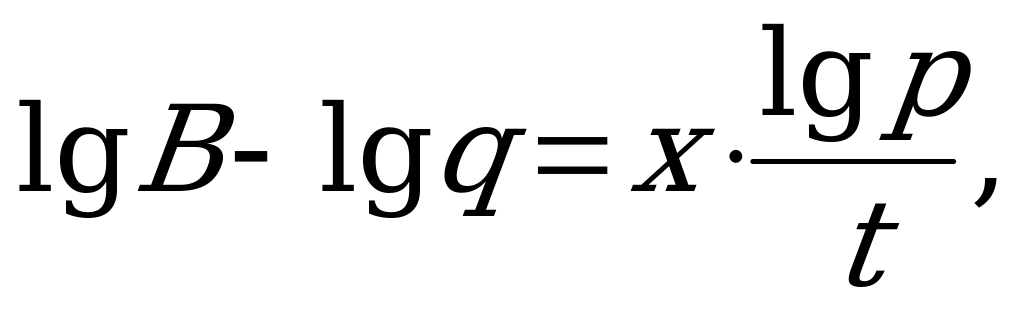
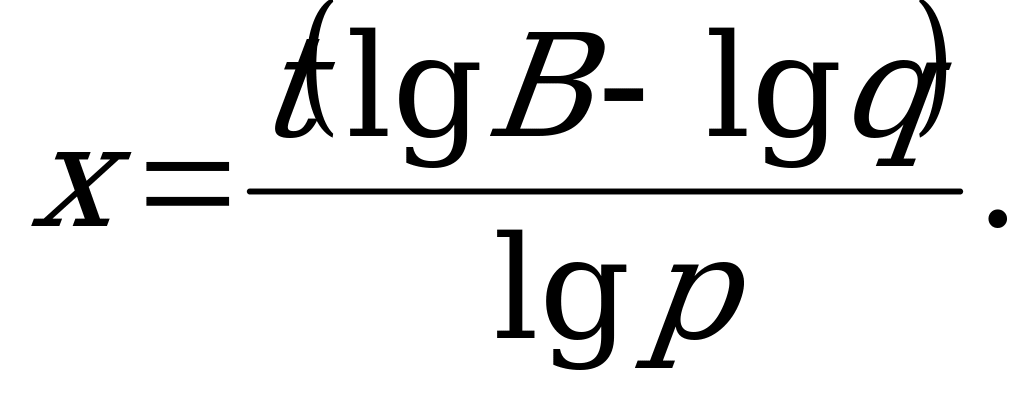
Ответ: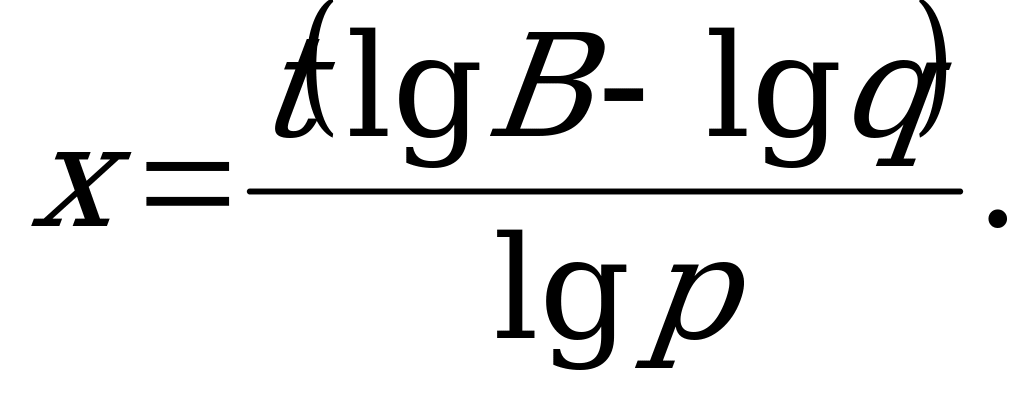

Заключение.

Итак, математика – это не только самостоятельная наука о “математических структурах”, но и язык других наук, язык единый, универсальный, точный, простой и красивый. Хорошо сказал об этих качествах математики советский математик С.Л.Соболев: “Есть одна наука, без которой невозможна никакая другая. Это математика. Ее понятия, представления и символы служат языком, на котором говорят, пишут и думают другие науки. Она объясняет закономерности сложных явлений, сводя их к простым, элементарным явлениям природы. Она предсказывает и предвычисляет далеко вперед с огромной точностью ход вещей.

Список используемой литературы.

1. Ресурсы Интернет

2. Симонов А.С. «Экономика на уроках математики»;

3. Москва, Школа-Пресс, 1999

4. Журнал «Математика в школе», №8 2002 год.

5. Математика. Приложение к газете «Первое сентября»,1997 год, № 4,5,6.

6. Сборник для подготовки к ЕГЭ по математике 2011 г.

7. Большая энциклопедия природы. Т. 16.Чудеса природы. М: ООО «Мир книги», 2003.

8. Васильева Т. С. Межпредметные связи школьного курса биологии // материалы IIIМеждунар. науч. конф. (г. Москва, июнь 2013 г.). — М.: Буки-Веди, 2013. — С. 72-75.

9. Кошель П. Энциклопедический словарь школьника. – М: ОЛМА-ПРЕСС, 2000.

10. Математическая статистика в биологии В. А. Медек, М. С. Токмачев (2007)

11. Реймерс Н.Ф. Основные биологические понятия и термины. – М: Просвещение, 1988.

12. Рогушина Т.П. «Интеграционный подход в обучении», газ. «Первое сентября», №7/2006

13. Сидоров А.М. Математические вычисления в биологии. Учебн. М. Энтропос-2013г.

11