Математические принципы золотого сечения

«Математические принципы золотого сечения»

Удивительное число. Что такое золотое сечение?

Все в нашем мире основано на числах. Некоторые из них имеют собственные имена. Среди всех этих замечательных чисел одно является особенно интересным: 1,6180339887… Список имен, данных этому числу, довольно длинен и показывает, с каким благоговением к нему относились: золотое число, божественное число, божественное сечение…. Принято называть его золотым сечением. Оно обозначается греческой буквой Ф (фи) и играет в математике выдающуюся роль, обладая удивительными свойствами и неожиданными связями с творениями природы и человека.

Число, равное отношению 1,6180339887, обычно обозначается прописной греческой буквой Ф в честь древнегреческого скульптора и архитектора Фидия.

Для практических целей ограничиваются приблизительным значением Ф = 1,618 или Ф = 1,62. В процентном округленном значении золотое сечение - это деление какой-либо величины в отношении 62% и 38%.

Что же такое - Золотое сечение? Золотое сечение или золотая пропорция, деление в крайнем и среднем отношении - отношение двух величин a и b, где a b, когда справедливо равенство 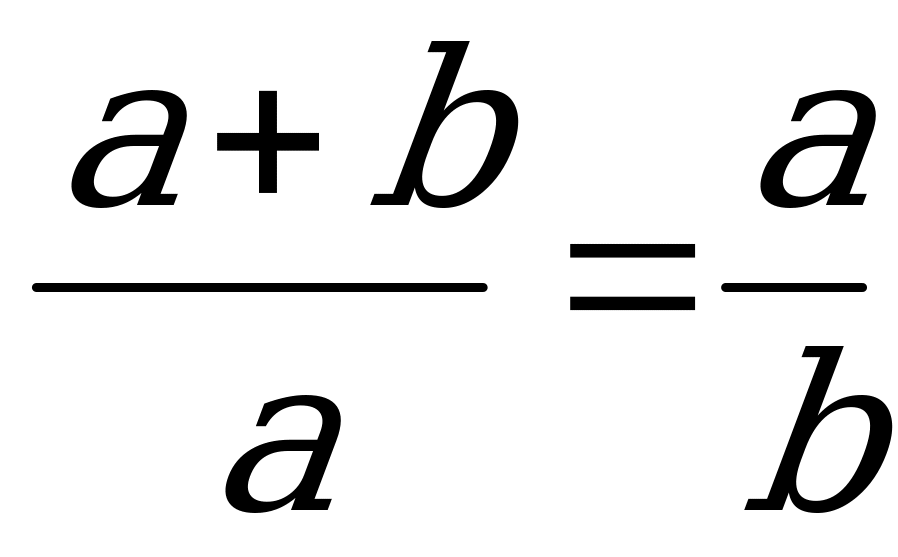. Данное отношение равно Ф, т.е. 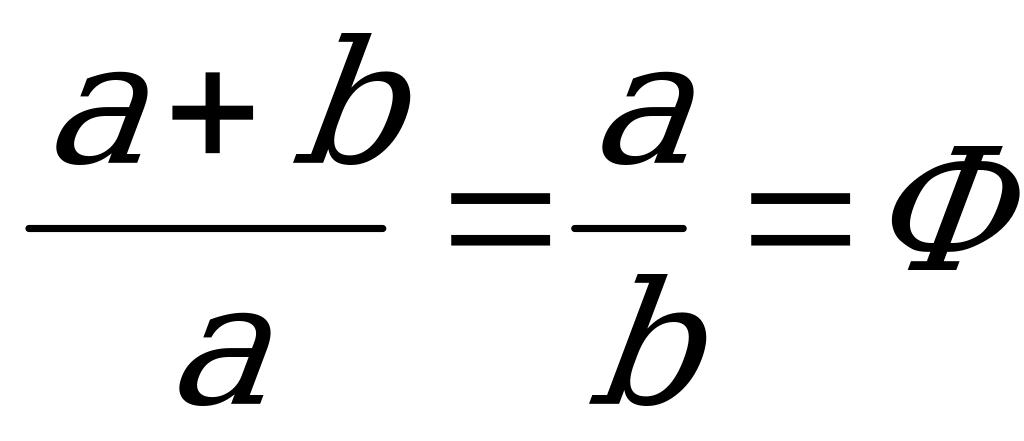. Этот термин впервые применил Леонардо да Винчи.

Рассмотрим на примере отрезка, изображенного на рисунке 1.

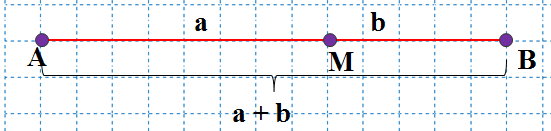
Рисунок 1.

У нас есть отрезок АВ, то в нем .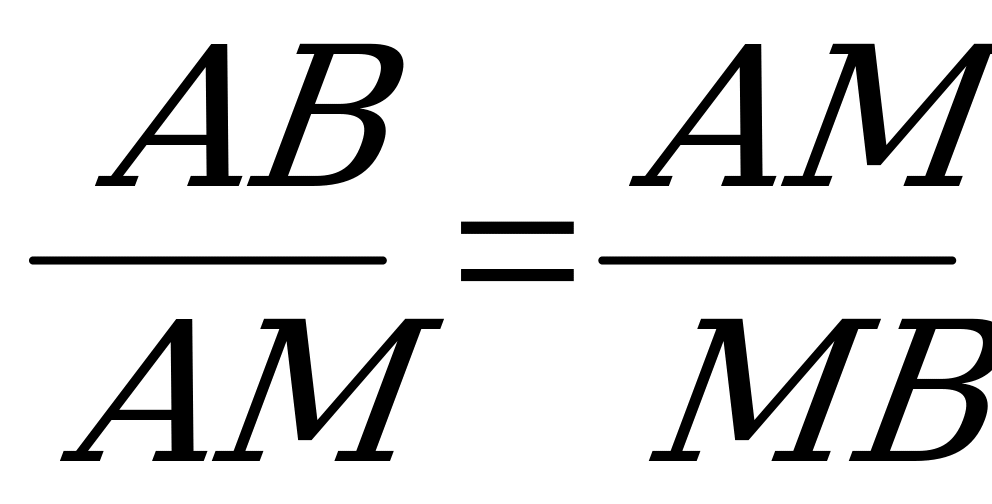

.

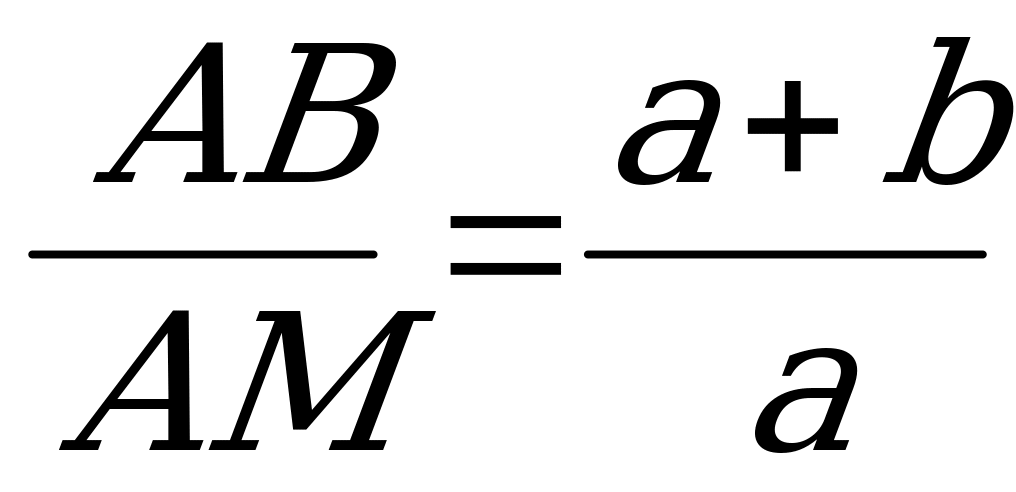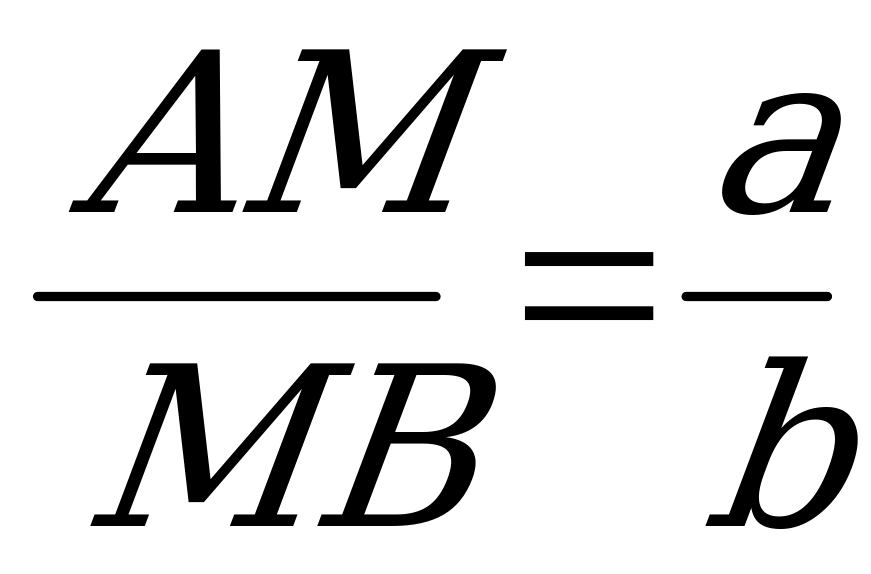
Как разделить отрезок в отношении Ф? Последовательность Фибоначчи

Такое построение с помощью циркуля и линейки описано уже в знаменитых «Началах» Евклида. Оно показано на рисунке 2.

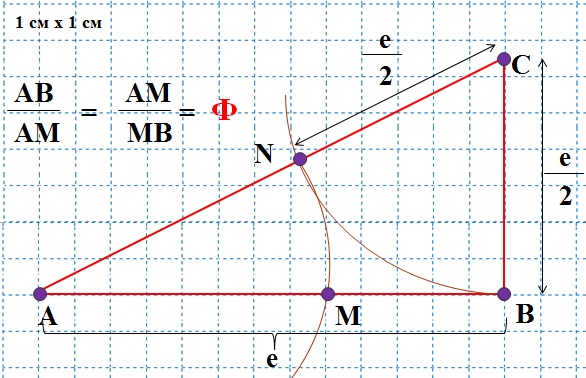
Рисунок 2

Сначала к отрезку AB восстановим перпендикуляр BC, длина которого равна половине длины отрезка AB. Затем проведем отрезок AC - это гипотенуза треугольника ABC. Далее изобразим две окружности: одну с центром в точке C и радиусом BC, а вторую- с центром в точке A и радиусом AN, где N точка пересечения первой окружности с отрезком AC. Точка M, в которой вторая окружность пересекает отрезок AB, делит его в отношении Ф, т.е.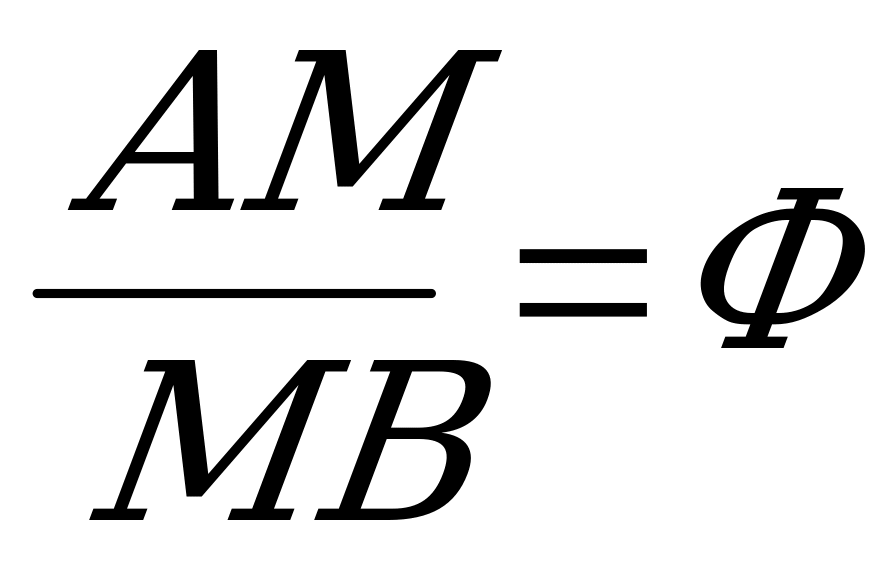

AB = e, ВС = е/2.

Используя эту схему.

1. Возьмём отрезок АВ = 13 см.

2. Найдём его половину: 6,5 см.

3. Проведём перпендикуляр, ВС = 6,5 см.

4. Соединим точки А и С.

5. Получили, что АМ = 8см, МВ = 5см.

6. Отношение: ; .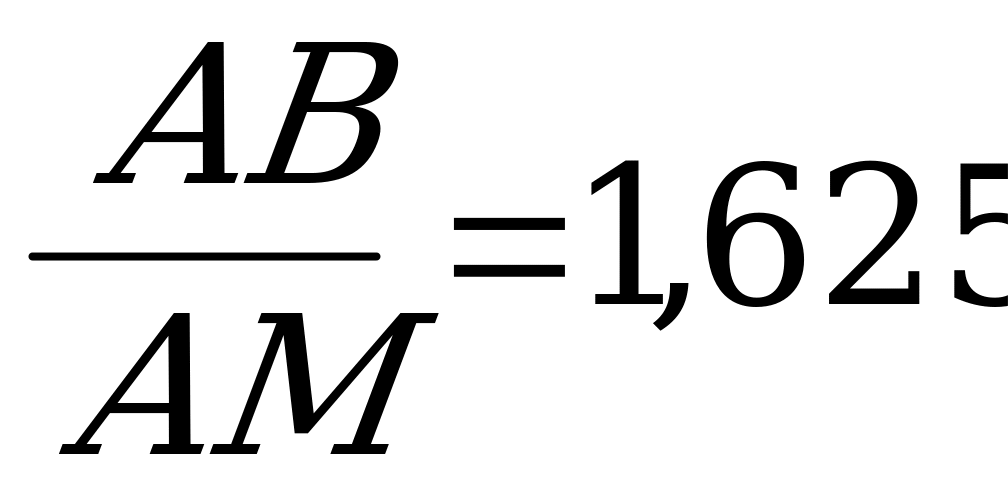

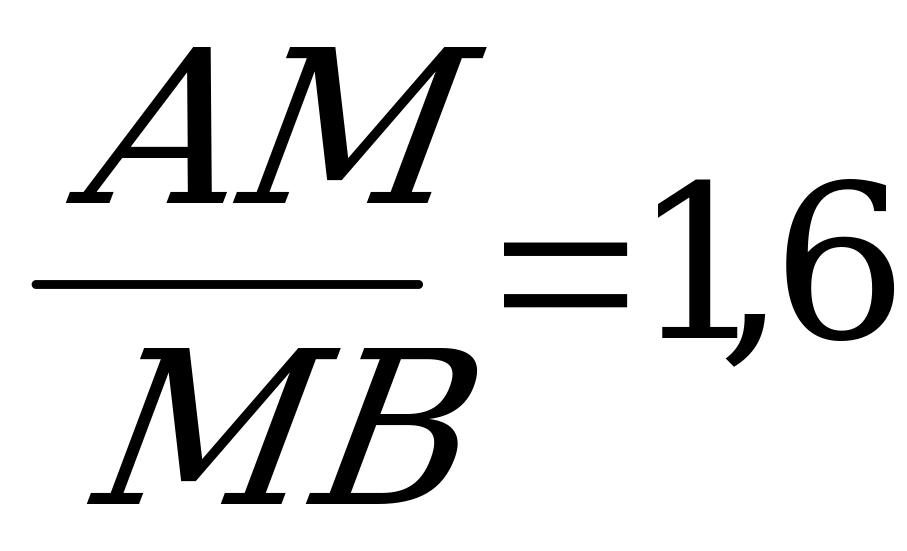Вывод: Отношения приблизительно равны числу Ф. Построение, находится в приложение 1 к работе.

Числа Фибоначчи — элементы последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … в которой первые два числа равны 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Так названы, в честь средневекового математика Леонардо Пизанского (около 1170 – около 1250) (известного как Фибоначчи).

Последовательность тесно связана с золотой пропорцией, потому что если вы берете какие-либо две последовательные цифры и делите на предыдущую, дробь окажется очень близкой к золотой пропорции. По мере увеличения значения числа, дробь становится еще ближе к золотой пропорции. Например:

3/2 = 1,5; 5/3 = 1,67; 8/5 = 1,6; 34/21 = 1,619 и так далее.

В нашем построение, получились числа из последовательности Фибоначчи!

Золотой прямоугольник

Стороны Золотого прямоугольника находятся в пропорции Ф к 1. Построим прямоугольник, используя, деление отрезка на рисунке 3.

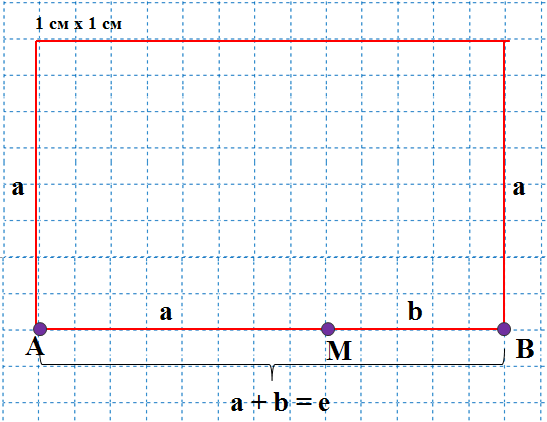
Рисунок 3

Обозначим за а длину отрезка АМ, а длину отрезка МВ за b. Так как длина отрезка AB = e, то е = а + b. Эти значения удовлетворяют следующему условию: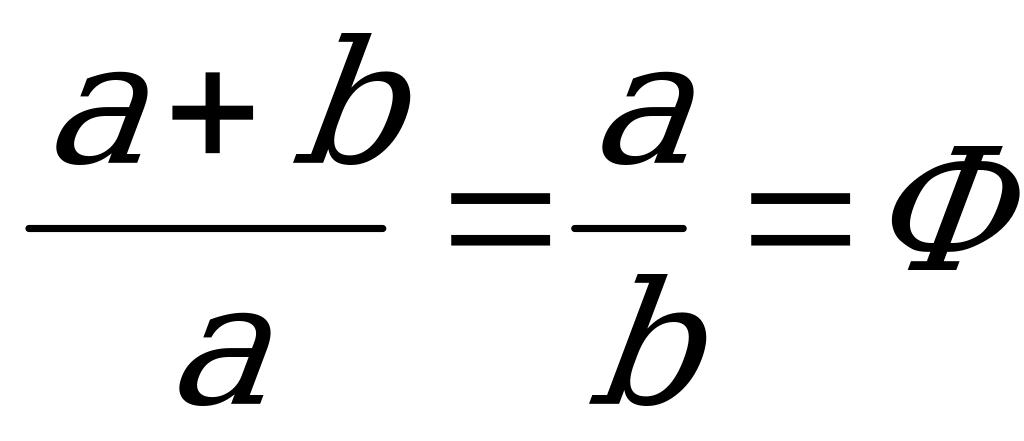

Этот прямоугольник называется «золотым».

Возьмем два одинаковых прямоугольника ABDE и BPTH. Поместим их рядом друг с другом, один горизонтально, другой вертикально, как на рисунке 4

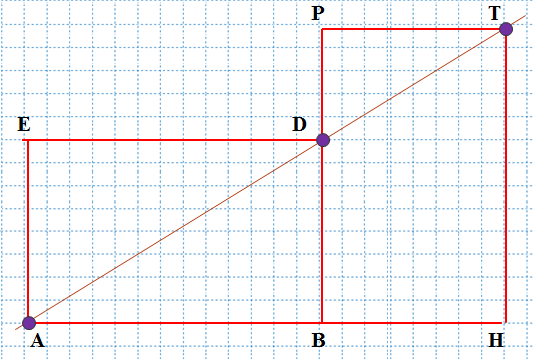
Рисунок 4

Затем проведем линию через вершины A и T как показано на рисунке 4. Если эта прямая проходит через вершину D, то прямоугольники ABDE и BPTH – «золотые прямоугольники».

Мы проверили этот признак на двух одинаковых прямоугольниках, для сторон которых не выполняется золотое сечение. Это показано на рисунке 5.

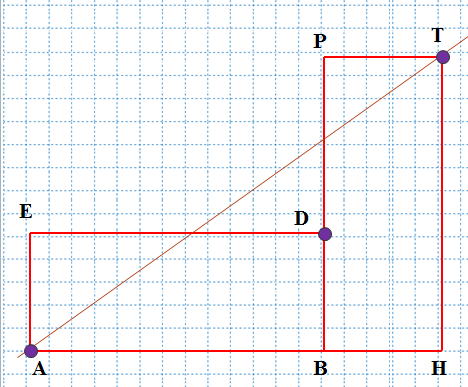
Рисунок 5

Вывод: Признак «золотого прямоугольника» удобно использовать, когда нет под рукой линейки. Прямую линию можно провести не только линейкой.

Присутствие золотого сечения в окружающей жизни

Золотые прямоугольники входят в основу «Кредитных карт». В наши дни большинство людей носит в кошельках и сумочках множество карточек: кредитные карты, визитные карточки. Мы пользуемся ими ежедневно, не обращая внимания на тот факт – вовсе неслучайный и немаловажный – что большинство карточек имеет одинаковый размер и форму, по крайней мере, те же пропорции. Чтобы убедится в этом, достаточно измерить и сравнить стороны карточек прямоугольников. Отношение большей стороны к меньшей в большинстве случаев является числом, очень близким к 1,618, числу Ф. Поэтому не случайно, что это отношение у большинства карт является одним и тем же, это стандартные размеры.

Сравнили: 8,2 см : 5,25 см = 1,619.

Если у Вас две кредитные карточки, то можно воспользоваться признаком «золотого прямоугольника». Проведем эксперимент.

Положим одну кредитную карту вертикально, а вторую – горизонтально, так, чтобы нижние их стороны были на одинаковой высоте, как показано на рисунке 6.

Мы видим, что линия проходит в точности через правый верхний угол карты – приятная неожиданность! Многие предметы созданы с помощью формулы «Золотого сечения» – даже, вполне вероятно, - книги!

Рисунок 6

Золотая спираль в природе

Золотой прямоугольник можно использовать для построения Золотой спирали.

Золотая спираль имеет уникальную форму и пропорции, широко встречающиеся в природе. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:

• практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;

• данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;

• именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания

Сосновые шишки, раковины улиток, раковины моллюсков, папоротники, паутина – все они образуют спирали.

Связь золотого сечения с телом человека

Если посмотреть внимательно на указательный палец, состоящий из трех фаланг, то отношение длины пальца к длине двух верхних фаланг и есть Золотое Сечение.

По мнению ученых, присутствие золотой пропорции в строении скелета решает очень важную задачу: достигается максимально возможная прочность остова при минимально возможном весе, что, в свою очередь, позволяет рационально распределить материю по частям тела.

Человеческое тело является воплощением Золотых сечений во всем от внешних размеров до устройства лица.

В теле человека, золотому сечению равны такие пропорции, как:

• Рост / расстоянию от талии до стоп

• Расстояние от талии до стоп / расстоянию от макушки до талии

• Высота лица / ширина лица

• Ширина рта / ширина носа

Золотое сечение в пропорциях тела человека

• Рост / расстояние от талии до стоп

• Расстояние от талии до стоп/ расстояние от макушки до талии

Отношения у человека около 1,61. Все, у кого значения близки к числу Ф, занимаются спортом или танцами.

Золотое сечение в чертах лица человека.

• Высота лица / ширина лица

• Ширина рта / ширина носа

Числа, выражающие отношения близки к числу Ф.

Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытий. Люди издавна пытались понять, почему одно кажется красивым, другое нет, искали закономерности. Была открыты математические принципы, которым подчиняется все, что мы называем красивым.

Мы видим красоту и широту «золотого сечения» в реальной жизни и выявить этот феномен в пропорциях тела человека и в окружающих предметах

6