Математический и пружинный маятники

МАТЕМАТИЧЕСКИЙ МАЯТНИК

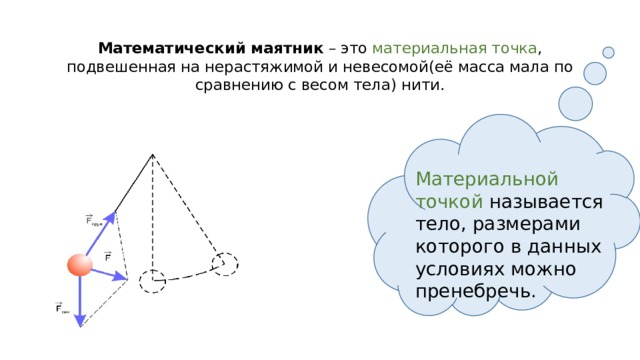
Математический маятник  – это материальная точка , подвешенная на нерастяжимой и невесомой(её масса мала по сравнению с весом тела) нити.

Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.

Условия

• При выведении его из положения равновесия в системе возникает сила, направленная к положению равновесия
• Трение в колебательной системе достаточччно мало

Зависимость Математического маятника

Галилео Галилей

(1564-1642гг.)

Великий итальянский ученый – один из создателей точного естествознания.

Учился сначала в монастырской школе, а затем в университете. Уже в студенческие годы Галилей увлекся изучением колебаний. Он обнаружил, что колебания маятника не зависят от его массы, а определяются длиной подвеса.

ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКА

• Период:

Христиа́н Гю́йгенс

g - Ускорение свободного падения

- Длина маятника(м)

(1629-1695гг.)

ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКА

• Период (T):

Христиа́н Гю́йгенс

g - Ускорение свободного падения(м/с2)

- Длина маятника(м)

(1629-1695гг.)

Характеристика Математического маятника

• Циклическая частота (число колебаний за 2  секунд):

• График устанавливает зависимость смещения тела со временем.

Практическое использование колебаний маятника

ИНТЕРЕСНЫЕ ФАКТЫ

МАТЕМАТИЧЕСКИЙ И ПРУЖИННЫЙ МАЯТНИКИ

Пружинный маятник.

• Маятник на пружине — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Характеристика Пружинных маятников

Закон Гука:

Сила упругости пропорциональна смещению тела (удлинению пружины):

Fупр = –kx.

k – коэффициент жесткости пружины.

x – отклонение груза от точки равновесия

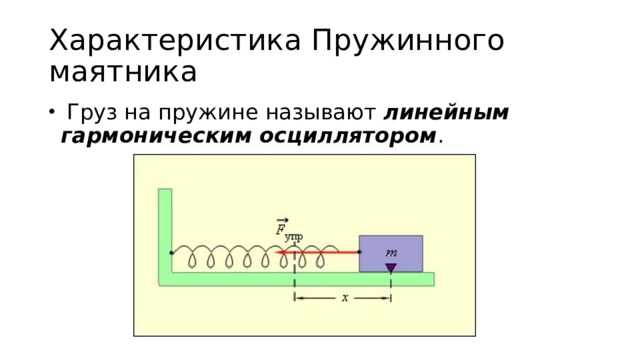
Характеристика Пружинного маятника

•   Груз на пружине называют  линейным гармоническим осциллятором .

Характеристика Пружинного маятника

Собственная частота ( ω 0  )

Период

(Т)

k – коэффициент жесткости пружины.

k – коэффициент жесткости пружины.

m – масса маятника.

m – масса маятника.

- математическая постоянная ≈ 3,14

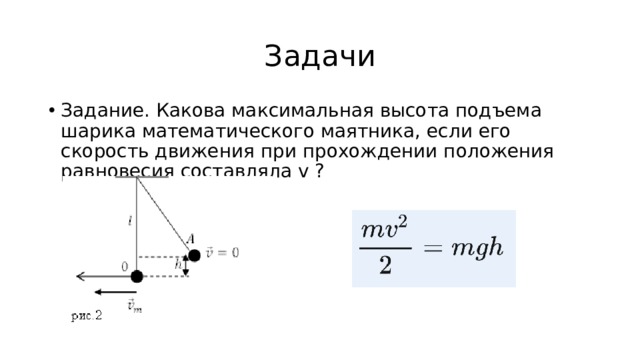
Задачи

• Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла v ?

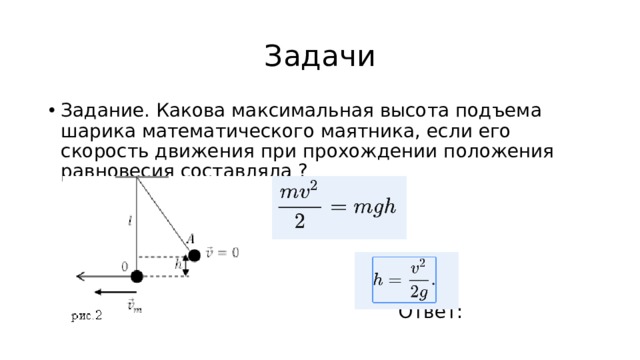
Задачи

• Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла ?

Ответ:

Задача

• Пример  .  Тело массой m=2 кг подвешено к упругой пружине, совершает гармонические колебания. Определите жёсткость k пружины, если за время t=1,5мин число N полных колебаний равно 60.
• Дано :  m=2кг ;  t=1,5мин=90с; N=60.
• Найти :  k.

Решение :  Период гармонических колебаний тела, подвешенного на пружине (пружинный маятник),

где m- масса тела; k- жёсткость пружины.

С другой стороны, период колебаний

где t – время, за которое совершается N полных колебаний.

Приравняв оба выражения

Найдём искомую жёсткость пружины

Ответ : k=35,1 Н/м.

СПАСИБО ЗА ВНИМАНИЕ