Математическое моделирование. Задача планирования производства.

Математическое моделирование

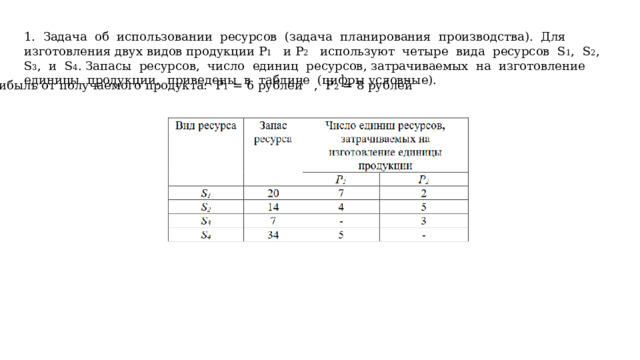
1. Задача об использовании ресурсов (задача планирования производства). Для изготовления двух видов продукции P 1 и P 2 используют четыре вида ресурсов S 1 , S 2 , S 3 , и S 4 . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (цифры условные).

Прибыль от получаемого продукта: P 1 = 6 рублей , P 2 = 8 рублей

Составим план производства продукции, при котором прибыль от ее реализации будет максимальной!

Для этого составим математическую модель и запишем обозначения:

1) X 1 и X 2 – это число единицы продукции

2) P 1 и P 2 – это продукция

ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X 1 , X 2 )

Сейчас мы составим математическое уравнение для каждого ресурса ( S 1 , S 2 , S 3 , S 4 )

P 1 (продукция) в паре с x 1 (продукция = неизвестная), а P 2 (продукция) в паре с x 2 (продукции = неизвестная)

= вот данные взятые из таблицы

S 1 = P 1 + P 2 ≤ S

Запас ресурса

Теперь подставляем значения формулы S 1 = P 1 + P 2 ≤ S = S 1 = 7 (x 1 ) + 2 (x 2 ) ≤ 20

ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X 1 , X 2 )

Сейчас мы составим математическое уравнение для каждого ресурса ( S1 , S2, S3, S4 )

P 1 (продукция) в паре с x 1 (продукция = неизвестная), а P 2 (продукция) в паре с x 2 (продукции = неизвестная)

= вот данные взятые из таблицы

S 2 = P 1 + P 2 ≤ S

Запас ресурса

Теперь подставляем значения формулы S 2 = P 1 + P 2 ≤ S = S 2 = 4 (x 1 ) + 5 (x 2 ) ≤ 14

ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X 1 , X 2 )

Сейчас мы составим математическое уравнение для каждого ресурса ( S1 , S2, S3, S4 )

P 1 (продукция) в паре с x 1 (продукция = неизвестная), а P 2 (продукция) в паре с x 2 (продукции = неизвестная)

= вот данные взятые из таблицы

S 3 = P 1 + P 2 ≤ S

Запас ресурса

Теперь подставляем значения формулы S 3 = P 1 + P 2 ≤ S = S 3 = ? (x 1 ) + 3 (x 2 ) ≤ 7

ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X 1 , X 2 )

Сейчас мы составим математическое уравнение для каждого ресурса ( S 1 , S 2 , S 3 , S 4 )

P1 (продукция) в паре с x 1 (продукция = неизвестная), а P2 (продукция) в паре с x 2 (продукции = неизвестная)

= вот данные взятые из таблицы

S 4 = P 1 + P 2 ≤ S

Запас ресурса

Теперь подставляем значения формулы S 4 = P 1 + P 2 ≤ S = S 4 = 5 (x 1 ) + ? (x 2 ) ≤ 34

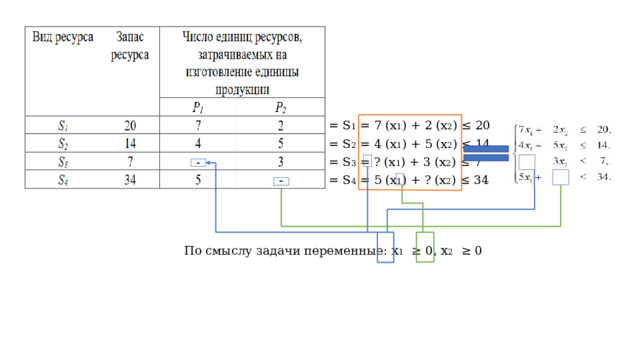
= S 1 = 7 (x 1 ) + 2 (x 2 ) ≤ 20

= S 2 = 4 (x 1 ) + 5 (x 2 ) ≤ 14

= S 3 = ? (x 1 ) + 3 (x 2 ) ≤ 7

= S 4 = 5 (x 1 ) + ? (x 2 ) ≤ 34

По смыслу задачи переменные: x 1 ≥ 0, x 2 ≥ 0

F – это суммарная прибыль.

F = P 1 (x 1 ) + P 2 (x 2 )

F = 6 (x 1 ) + 8 (x 2 )

Экономико-математическая модель задачи: найти такой план выпуска продукции Х=(x 1 ,x 2 ), удовлетворяющий системе (1.1) и условию (1.2), при котором функция (1.3) принимает максимальное значение.

(1.1)

(1.2)

(1.3)

F = 6 (x 1 ) + 8 (x 2 )

X 1 ≥ 0, x 2 ≥ 0

Задачу легко обобщить на случай выпуска n видов продукции с использованием m видов ресурсов.

Предприятие для производства n видов продукции использует m видов ресурсов.

Известно, нормы затрат ресурсов для производства единицы продукции каждого вида:

a (ij) - норма затрат,

i – ого ресурса для производства единицы продукции,

j – ого вида .

Составим экономико-математическую модель задачи:

m видов ресурсов

a (ij) - норма затрат

i – одного ресурса для производства единицы продукции

j – одного вида продукции

B – объём ресурсов у предприятия

Cj – производимая продукция реализуемая в цене

N – виды продукции

Вид продукции = 1, вид продукции

Прибыль = вид продукции * (х1) + (прибыль от единицы продукта) (х2) + …

(прибыль от единицы продукта) вид продукции х вид продукции =

(прибыль от единицы продукта) вид продукции * х вид продукции

норма затрат * неизвестный вид продукции ≤ ограниченный вид ресурс,

Одного ресурса на единицу ресурса = 1, видов ресурса

Так как при решении результат может получиться отрицательным, то для решения необходимо обязательно использовать условия не отрицательности проектных параметров х. Нужно для избежание ошибки!

неизвестный вид продукции ≥ 0, вид продукции = 1, вида продукции.

Замечания:

1. В модели не учтены емкость рынка и объем поступивших заказов.

Учет этих факторов рынка можно записать в виде ограничений , где

dj- объем заказов

Dj - предельная емкость рынка

j - ой продукции.

2. Оптимальный объем и номенклатура производства могут определяться не только первоначальными запасами ресурсов , но и объемом выделенных финансов на производство Q . Тогда ограничения на ресурсы и финансы запишутся в виде следующих неравенств:

- цены на ресурсы

Таким образом, был рассмотрен план производство продукции, изготовление продукции, вычитывали максимальную прибыль и учёт с отрицательным значением

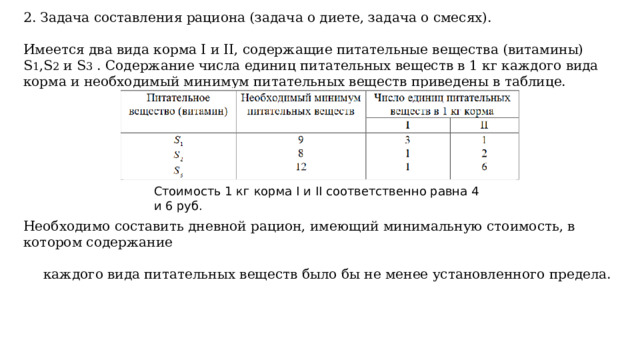
2. Задача составления рациона (задача о диете, задача о смесях).

Имеется два вида корма I и II, содержащие питательные вещества (витамины) S 1 ,S 2 и S 3 . Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице.

Стоимость 1 кг корма I и II соответственно равна 4 и 6 руб.

Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание

каждого вида питательных веществ было бы не менее установленного предела.

x 1 и x 2 – количество кормов I и II

S – единица питательных веществ

S 1 = I (x 1 ) + 1 * (x 2 ) =

S 2 = I (x 1 ) + 1 * (x 2 ) =

S 3 = I (x 1 ) + 1 * (x 2 ) =

Так как содержание питательных веществ S 1 ,S 2 и S 3 в рационе должно быть не менее соответственно 9, 8 и 12 единиц, то получим систему неравенств:

Комментарий: 1 убираем, а также переменные x 1 и x 2 должны быть больше 0

Рассчитаем стоимость рациона в (рублях)

Экономико-математическая модель задачи: составить дневной рацион , удовлетворяющий системе (1.4) и условию (1.5), при котором функция (1.6) принимает минимальное значение.

(1.4)

(1.5)

(1.6)

Для формулировки задачи в общей постановке обозначим: , число единиц корма n-го вида;

,, необходимый минимум содержания в рационе питательного вещества , число единиц питательного вещества , в единице корма j-го вида; cj - стоимость единицы корма j - го вида.

Экономико-математическая модель задачи примет вид:

Найти такой рацион X = ( x 1 , x 2 , … x n ) удовлетворяющий системе

3. Задача об использовании мощностей (задача о загрузке оборудования).

Предприятию задан план производства продукции по времени и номенклатуре: требуется за время T выпустить n 1 , n 2 , ..., n k единиц продукции Р 1 , P 2 , ..., P k .

Продукция производится на станках S 1 , S 2 , ..., S m .

Для каждого станка известны производительность а ij (т.е. число единиц продукции P j , которое можно произвести на станке S i ) и затраты b ij на изготовление продукции Р j

на станке S i в единицу времени.

Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.

Составим экономико-математическую модель задачи.

Обозначим - время , в течение которого станок

будет занят изготовлением продукции

Так как время работы каждого станка ограничено и не превышает Т, то справедливы неравенства:

Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства:

Затраты на производство всей продукции выразятся функцией

Экономико-математическая модель задачи об использовании мощностей примет вид: найти такое решение , , удовлетворяющее системам (1.7) и (1.8) и условию (1.9), при котором

функция (1.10) принимает минимальное значение.

4. Задача о раскрое материалов.

На раскрой (распил, обработку) поступает материал одного образца в количестве а единиц.

Требуется изготовить из него l разных комплектующих изделий в количествах, пропорциональных числам

, (условие комплектности). Каждая единица материала может быть раскроена n различными способами, причем использование -го способа дает единиц k-го изделия

Необходимо найти план раскроя, обеспечивающий максимальное число комплектов.

Экономико-математическая модель задачи:

Обозначим - число единиц материала, раскраиваемых I-м способом, и х - число изготавливаемых комплектов изделий.

Так как общее количество материала равно сумме его единиц, раскраиваемых различными способами, то

Требование комплектности выразится уравнениями

Очевидно, что

(1.12)

(1.13)

Экономико-математическая модель задачи: найти такое решение Х=(х 1 , х 2 … x n ), удовлетворяющее системе уравнений (1.11) и (1.12) и условию (1.13), при котором функция F= х принимает максимальное значение .

Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступают 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Составить экономико-математическую модель задачи.

Решение. Определим всевозможные способы распила бревен, указав соответствующее число получаемых при этом брусьев.

Число получаемых брусьев длиной, м

Способ распил I

1,2

3,0

5,0

-

1

-

5

-

1

2

-

-

2

-

1

-

2

3

4

Пусть - число бревен, распиленных м способом ( = 1,2,3,4); х- число комплектов брусьев.

Учитывая, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, экономико-математическая модель задачи примет вид:

Задачу о раскрое легко обобщить на случай т раскраиваемых материалов.

Пусть каждая единица -го материала может быть раскроена n различными способами,

причем использование -го способа даёт единиц k-го изделия ,

а запас j-го материала равен единиц.

Обозначим число единиц j-гo материала, раскрываемого -м способом.

Экономико-математическая модель задачи о раскрое в общей постановке примет вид: найти такое решение

, удовлетворяющее системе

и условию , при котором функция F=x принимает максимальное значение.

5. Транспортная задача

Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям, при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем, потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. От схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.

Задача формулируется так: имеется m пунктов производства, в каждом из которых сосредоточено

, единиц однородного продукта. Этот продукт нужно доставить n потребителям, где потребность составляет b j ( ) единиц. Причем

Известны величины – затраты на перевозку единицы продукта из - го пункта производства в j-ый пункт потребления. Обозначим через количество продукта, перевозимое из -гo пункта производства в j-ый пункт потребления. Матрица называется матрицей тарифов.

Матрица

Математическая модель транспортной задачи: целевая функция, описывающая транспортные затраты:

, минимизируется при ограничениях на возможности поставщиков: весь родукт из пункта производства должен быть вывезен:

,

на спрос потребителей, который должен быть удовлетворен:

при условии не отрицательности переменных, исключающем обратные перевозки:

Детерминированные задачи Задачи динамического программирования

Общая постановка задачи динамического программирования

Динамическое программирование (ДП) – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.

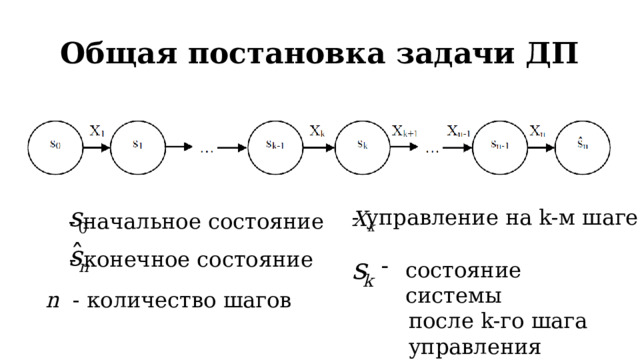
Общая постановка задачи ДП

- управление на k-м шаге

- начальное состояние

- конечное состояние

• состояние системы

после k-го шага

управления

n - количество шагов

– управление, переводящее систему S

из состояния s 0 в состояние ŝ

– Показатель эффективности

рассматриваемой управляемой

операции – целевая функция –

зависит от начального состояния и

управления

(6.1)

Основные предположения модели ДП

1. Состояние s k системы в конце k-го шага зависит только от предшествующего состояния s k-1 и управления на k-м шаге X k (и не зависит от предшествующих состояний и управлений). Это требование называется "отсутствием последействия". Сформулированное положение записывается в виде уравнений, которые называются уравнениями состояний :

(6.2)

2. Целевая функция (6.1) является аддитивной от показателя эффективности каждого шага.

Показатель эффективности k-го шага:

(6.3)

Целевая функция:

(6.4)

Задача ДП формулируется так : определить такое допустимое управление Х, переводящее систему S из состояния s 0 в со-

стояние ŝ, при котором целевая функция (6.4) принимает наибольшее (наименьшее) значение.

Особенности модели ДП

1. Задача оптимизации интерпретируется как n-шаговый процесс управления.

2. Целевая функция равна сумме целевых функций каждого шага.

3. Выбор управления на k-м шаге зависит только от состояния системы к этому шагу, не влияет на предшествующие шаги (нет обратной связи).

4. Состояние s k после k-го шага управления зависит только от предшествующего состояния s k-1 и управления X k (отсутствие последействия).

5. На каждом шаге управление X k зависит от конечного числа управляющих переменных, а состояние s k – от конечного числа параметров.

Принцип оптимальности и уравнения Беллмана

Принцип оптимальности впервые был сформулирован

Р. Беллманом в 1953 г.

Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Основное требование – процесс управления должен быть без обратной связи.

Уравнения Беллмана

Вместо исходной задачи ДП с фиксированным числом шагов n и начальным состоянием s 0 рассмотрим последовательность задач, полагая последовательно n = 1, 2, … при различных s –

одношаговую, двухшаговую и т.д., – используя принцип оптимальности.

Рассмотрим n-й шаг:

s n-1 – состояние системы к началу n-го шага,

s n = ŝ – конечное состояние,

X n – управление на n-м шаге,

f n (s n-1 , X n ) – целевая функция (выигрыш) n-го шага.

Согласно принципу оптимальности, X n нужно выбирать так, чтобы для любых состояний s n-1 получить максимум целевой функций на этом шаге.

максимум целевой функции – показателя эффективности n-го шага при условии, что к началу последнего шага, система S была в произвольном состоянии s n-1 , а на последнем шаге управление было оптимальным (условный максимум целевой функции).

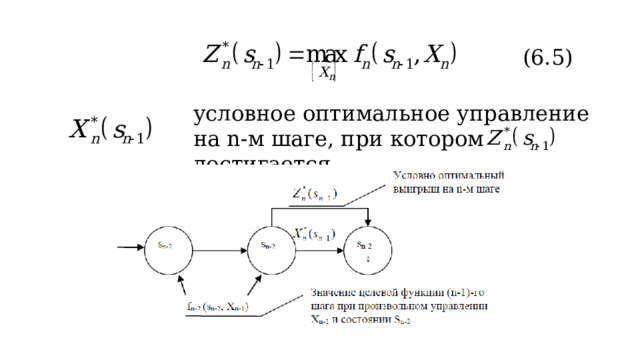
(6.5)

условное оптимальное управление на n-м шаге, при котором достигается .

Рассмотрим теперь двухшаговую задачу: присоединим к n-му шагу (n-1)-й.

Для любых состояний s n-2 произвольных управлений X n-1 и оптимальном управлении на n-м шаге значение целевой функции на двух последних шагах равно:

(6.6)

Согласно принципу оптимальности для любых s n-2 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (n-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (6.6) по всем допустимым управлениям Х n-1 .

(6.7)

условный максимум целевой функции при оптимальном управлении на двух последних шагах

Управление на (n-1)-м шаге называется условным оптимальным управлением на (n-1)-м шаге и обозначается через .

выражение, стоящее в фигурных скобках (6.7), зависит только от s n-2 и Х n-1 , так как s n-1 можно найти из уравнения состояний (6.2) при k = n – 1

и подставить вместо s n-1 в функцию .

В результате максимизации только по одной переменной Х n-1 согласно уравнению (6.7) вновь получаются две функции:

Далее рассматривается трехшаговая задача: к двум последним шагам присоединяется (n-2)-й и т. д.

условный максимум целевой функции, полученный при оптимальном управлении

на n – k + 1 шагах, начиная с k-го до конца, при условии, что к началу k-го шага система находилась в состоянии s k-1

тогда

Целевая функция на n – k последних шагах при произвольном управлении X k на k-м шаге и оптимальном управлении на последующих n – k шагах равна

Согласно принципу оптимальности, Х k выбирается из условия максимума этой суммы (Уравнения Беллмана):

(6.8)

условное оптимальное управление на k-м шаге

Процесс решения уравнений (6.5) и (6.8) называется условной оптимизацией

В результате условной оптимизации получаются две последовательности:

условные максимумы целевой функции на последнем, на двух последних, … n шагах

условные оптимальные управления на n-м, (n – l)-м, ..., 1-м шагах

Используя эти последовательности, можно найти решение задачи ДП при данных n и s 0 .

условный максимум целевой функции за N шагов при условии, что к началу 1-го шага система была в состоянии s 0

(6.9)

Далее следует использовать последовательность условных оптимальных управлений и уравнения состояний (6.2).

При фиксированном s0 получаем

Далее из уравнений (6.2) находим

подставляем это выражение в последовательность условных оптимальных управлений и т.д. по цепочке

Нахождение кратчайших путей в графе. Решение задачи о максимальном потоке.

Содержание материала: задача о нахождении кратчайших путей в графе. Задача о нахождении максимального потока.

Краткие теоретические основания выполнения задания

Граф — это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными. Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом. Если ребра не имеют ориентации, граф называется неориентированным.

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра - линиями, соединяющими точки (рис. 1).

Петля это дуга, начальная и конечная вершина которой совпадают.

Простой граф - граф без кратных ребер и петель.

Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

Пустым называется граф без ребер. Полным называется граф, в котором каждые две

вершины смежные.

Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

Маршрут в графе путь, ориентацией дуг которого можно пренебречь.

Цепь маршрут, в котором все ребра попарно различны.

Цикл замкнутый маршрут, являющийся цепью.

Маршрут, в котором все вершины попарно различны , называют простой цепью . Цикл, в котором все вершины, кроме первой и последней , попарно различны , называются простым циклом .

Подграф графа это граф, являющийся подмоделью исходного графа, т.е. подграф содержит некоторые вершины исходного графа и некоторые ребра (только те, оба конца которых входят в подграф).

Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа.

Граф называется связным , если любая пара его вершин связана. Связными компонентами графа называются подграфы данного графа, вершины которых связаны.

Дерево — это связный граф без циклов. Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеалогические деревья.

Граф без цикла называется лесом . Вершины степени 1 в дереве называются листьями . Деревья - очень удобный инструмент представления информации самого разного вида. Деревья отличаются от простых графов тем, что при обходе дерева невозможны циклы . Это делает графы очень удобной формой организации данных для различных алгоритмов.

Очевидно, что графический способ представления графов непригоден для ПК. Поэтому существуют другие способы представления графов.

В теории графов применяются

• Матрица инцидентности. Это матрица А с n строками, соответствующими вершинам, и m столбцами, соответствующего рёбрам. Для ориентированного графа столбец, соответствующий дуге (х,y) содержит - 1 в строке, соответствующей вершине х и 1 , в строке, соответствующей вершине у . Во всех остальных 0 . Петлю, т.е. дугу (х,х) можно представлять иным значением в строке х , например, 2 . Если граф неориентированный, то столбец, соответствующий ребру (х,у) содержит 1 , соответствующие х и у и нули во всех остальных строках.
• Матрица смежности . Это матрица n×n где n - число вершин, где b ij = 1 , если существует ребро, идущее из вершины х в вершину у и b ij = 0 в противном случае.

Нахождение минимального остова в графе

Алгоритм решения

• Упорядочить ребра графа по возрастанию весов;
• Выбрать ребро с минимальным весом, не образующее цикл с ранее выбранными ребрами. Занести выбранное ребро в список ребер строящегося остова;
• Проверить, все ли вершины графа вошли в построенный остов. Если нет, то выполнить пункт 2 .

Нахождение кратчайшего пути в графе

Пусть дан граф, дугам которого приписаны веса. Задача о нахождении кратчайшего пути состоит в нахождении кратчайшего пути от заданной начальной вершины до заданной конечной вершины, при условии, что такой путь существует.

Данная задача может быть разбита на две:

• для начальной заданной вершины найти все кратчайшие пути от этой вершины к другим;

найти кратчайшие пути между всеми парами вершин.

2. найти кратчайшие пути между всеми парами вершин.

Рассмотрим алгоритм решения для задачи первого типа:

Необходимо найти путь от s - начальной вершины до t - конечной вершины. Каждой вершине присваиваем пометки I(Xi) .

• I(s) = 0, I(Xi) равно бесконечности для всех Хi не равных s и считать эти пометки временными. Положить р = s .
• Для всех Хi , принадлежащих Г(р) и пометки которых временны, изменить пометки по следующему правилу: I(Xi) = min[I(Xi), I(p) + c(p, Xi)]
• среди всех вершин с временными пометками найти такую, для которой I(Xi*) = min[I(Xi)]
• считать пометку вершины Хi* постоянной и положить р = Хi* .
• если р = t , то I(р) является длинной кратчайшего пути, если нет, перейти к шагу 2 .

Как только все пометки расставлены, кратчайшие пути получают, используя соотношение I(Xi') + c(Xi',Xi) = I(Xi) (1) .

Для решения задачи второго типа можно применять данный алгоритм для каждой вершины.

Задачи в условиях неопределенности.

• Системы массового обслуживания: понятия, примеры, модели.
• Основные понятия теории марковских процессов: случайный процесс, марковский процесс, граф состояний, поток событий, вероятность состояния, уравнения Колмогорова, финальные вероятности состояний.
• Схема гибели и размножения.
• Метод имитационного моделирования. Единичный жребий и формы его организации. Примеры задач
• Понятие прогноза. Количественные методы прогнозирования: скользящие средние, экспоненциальное сглаживание, проектирование тренда. Качественные методы прогноза
• Предмет и задачи теории игр. Основные понятия теории игр: игра, игроки, партия, выигрыш, проигрыш, ход, личные и случайные ходы, стратегические игры, стратегия, оптимальная стратегия.
• Антагонистические матричные игры: чистые и смешанные стратегии.
• Методы решения конечных игр: сведение игры mxn к задаче линейного программирования, численный метод – метод итераций.
• Область применимости теории принятия решений. Принятие решений в условиях определенности, в условиях риска, в условиях неопределенности. Критерии принятия решений в условиях неопределенности. Дерево решений.

Составление систем уравнений Колмогорова. Нахождение финальных вероятностей. Нахождение характеристик простейших систем массового обслуживания.

Марковский случайный процесс

Построение математических моделей в условиях неопределенности - очень сложная или невыполнимая задача. Лишь для некоторых упрощенных случаев можно построить математическую модель.

Следует различать два вида неопределенности:

• вероятностные характеристики либо известны, либо могут быть получены в результате эксперимента. Такая неопределенность называется стохастической, и для большинства объектов, содержащих такую неопределенность, можно построить математическую модель, например выход из строя оборудования, приход нового клиента и т. д.
• вероятностные характеристики определить невозможно. В этом случае задачу можно попытаться решить с помощью экспертных оценок, но результат будет весьма приблизительным, например, каковы будут модели женской одежды через пять лет?

Строгую математическую модель с аналитическим вычислением всех интересующих величин можно построить только в том случае, если случайный процесс носит марковский характер.

Случайный процесс будет марковским, если вероятностные характеристики процесса в момент времени t зависят только от текущего (настоящего) состояния процесса в этот момент времени t и не зависят от того, как (каким способом и когда) рассматриваемый процесс перешел в текущее состояние.

Из всего многообразия марковских процессов хорошо изучены и представляют большой практический интерес марковские случайные процессы с дискретными состояниями и непрерывным временем.

Суть имитационного моделирования

Имитационное моделирование  – получение экспериментальной информации о сложном объекте, которая не может быть получена иным путем, как экспериментируя с его моделью на ПЭВМ.

Как остроумно подметил Ю. Адлер, сочетание слов имитация и моделирование недопустимо и является тавтологией. Но, рассматривая исторический процесс формирования этого термина, пришли к выводу, что это словосочетание определяет в моделировании такую область, которая  относится к получению экспериментальной информации о сложном объекте, которая не может быть получена иным путем, как экспериментируя с его моделью на ПЭВМ .

Имитационный объект имеет вероятностный характер функционирования. Для исследователя представляют интерес выводы, носящие характер статистических показателей, оформленных, может быть, даже в виде графиков или таблиц, в которых каждому варианту исследуемых параметров поставлены в соответствие определенные средние значения с набором характеристик их распределения, без получения зависимости в аналитическом виде.

Эта особенность является и достоинством, и одновременно, недостатком имитационным моделей.  Достоинство  в том, что резко расширяется класс изучаемых объектов, а  недостаток  – в отсутствии простого управляющего выражения, позволяющего прогнозировать результат повторного эксперимента. Но в реальной жизни также невозможно для сколько-нибудь сложного объекта получить точное значение экономического показателя, а только лишь его ожидаемое значение с возможными отклонениями.