Matematika 4-nji synp

IV SYNP

MATEMATIKA

IV synpda matematika sapaklaryna bolan esasy talaplar

Mugallym IV synpda täze maksatnama boýunça işlemek üçin I-III synplaryň täze maksatnamalaryny, şeýle hem şol maksatnamalaryň düşündiriş hatlaryny oňat bilmelidir. Mundan başga-da, matematika mugallymlary täze okuw kitabyny we usuly gollanmalary çuň öwrenmelidirler.

Sapaklar meýilnamalaşdyrylanda mugallym şol sapakda öwreniljek maglumatlaryň ozal öwrenilen maglumatlar bilen, şeýle hem soň öwreniljek maglumatlar bilen baglanyşygyny kesgitlemelidir, öwrenilýän maglumatyň IV synpdaky ornuny anyklamalydyr, esasy we ikinji derejeli meseleler tapawutlandyrylmalydyr we şonuň esasynda sapagyň maksady kesgitlenilmelidir.

IV synpyň okuwçylary bilen işlenilende wagty tygşytlamak baradaky alada mugallymyň hemişelik aladalarynyň biri bolmalydyr. Mugallym temany gysgadan aýdyň düşündirmelidir, sapagyň temasyna degişli görkezme esbaplary, gerekli gurallary öňünden taýýarlamalydyr, käbir halatlarda çyzgylary çyzyp goýmalydyr. Çyzgy çyzylýarka okuwçynyň gatnaşmagy onuň çyzygyny oňat kabul edýändigi göz öňünde tutulmalydyr. Şonuň üçin hem, çyzgylary sapakdan öň taýýarlamaga aşa köp gyzyklanmaly däldir.

IV synpda matematikany okatmagyň maksatlarynyň biri-de okuwçylaryň döredijilikli ukybyny ösdürmekden ybaratdyr. Bu bolsa matematika sapaklarynda meseleleri çözmegiň dürli usullary arkaly gazanylýar. Mugallym şol bir meseläniň çözülişiniň dürli usullaryny deňeşdirip, olardan has gysga hem owadanyny saýlap, okuwçylarda meseläni gelşikli hem owadan çözmek barada düşünjäni emele getirmeli, olarda gözellik duýgyny terbiýelemeli.

Sapaklarda özbaşdak işleri geçirmek okuwçylara matematiki bilimlere we endiklere has düşünjeli eýe bolmaga, olary ulanmagy öwrenmäge kömek edýär. Bu maksatlara ýetmek üçin köp özbaşdak işler ýerine ýetirilýän döwründe okuwçylaryň okuw kitabyna, depderdäki öz ýazgylaryna, mugallymyň kömegine, erkin ýüz tutmagy, kämahallarda bolsa ýoldaşlary bilen erkin pikir alyşmagy wajypdyr. Şunuň ýaly maksatlar okuw kitabynda berlen meseleleri okuwçylaryň özbaşdak çözmegi hem okuw kitaby boýunça çylşyrymly bolmadyk soraglary özbaşdak öwrenmegi bilen gazanylýar.

Matematika sapagyna edilýän möhüm talap synpyň okuwçylary bilen, aýry-aýry okuwçylar bilen edilýän işi utgaşdyrmakdyr. Okuwçylar sapakda öwrenilýän maglumatlary dürli hili özleşdirýärler, olaryň bilim derejeleri dürlüdir. Şoňa görä-de, diňe bir bilim derejeleri gowşak bolan okuwçylar bilen däl-de eýsem güýçli okuwçylar bilen hem aýratynlykda iş geçirmek zerurdyr. Mugallymyň gös-göni borjy has gowşak okuwçylara aýratyn üns bermekden, olara hemişe kömek etmekden, ýetişmezligiň öňüni almakdan ybaratdyr. Bu hili kömegi, köplenç, sapakda amala aşyrmalydyr. Has güýçli okuwçylar bilen sapakda, aýratynlykda işlemek, esasan, olar üçin gyzykly we has çylşyrymly meseleleri saýlap almakdan ybaratdyr. Şeýle meseleler okuw kitabynyň “O” belgili we “Has kyn meseleler” bölümleriniň meselelerinden alnyp bilner.

Mugallym sapakda bilim bermeklige işeňňir ýolbaşçylyk etmelidir. Okuwçylaryň jogaplaryny, haýsy bolsa-da, bir meseläni çözmek baradaky teklipleri, okuw kitabynyň tekstini ara alyp maslahatlaşmak -- bularyň hemmesi bilim bermegiň elementleri bolup, olaryň taýýarlanyşynyň hili diňe mugallyma baglydyr.

Matematika sapaklarynda okuwçylaryň sözleýişini ösdürmek

Matematika sapaklarynda mugallym okuw maglumatlaryny düşündirmeli, ýerine ýetirilen gönükmelere düşündiriş bermeli, soraglar bermeli, okuwçylaryň jogaplaryny ara alyp maslahatlaşmaly bolýar. Bu işleriň üstünlikli geçmegi hem mugallymyň şol işleri guramagy başaryşyna bagly bolýar. Sapagy alyp barmakda mugallymyň sözleýşiniň uly ähmiýeti bar.

Mugallymyň sözleýşi pert, düşnükli, ýeterlik derejede belent, edebi taýdan sowatly bolmalydyr.

Mugallym öz göreldesi bilen okuwçylaryň matematiki sözleýiş diliniň ösmegine ýardam etmegi örän möhümdir.

IV synpda täze maksatnamanyň girizilmegi mugallymyň düşündirişlerinde täze matematiki adalgalary ulanmaklaryny talap edýär. Mugallym şol adalgalary dogry, takyk basym bilen aýtmalydyr.

Okuwçylaryň sözleýiş diline okuwyň ilkinji günlerinden başlap, berk hem gyşarnyksyz talap goýulmalydyr. Okuwçylara öz pikirini dogry aýtmagy öwretmek IV synpda matematikany okatmagyň iň möhüm meseleleriniň biridir. .

Tejribäniň görkezişi ýaly, okuwçylaryň umumy dil medeniýetini, matematiki sözleýişini ösdürmek üçin aşakdaky işleriň geçirilmegi peýdalydyr.

1.Sapaklarda matematiki aňlatmalaryň, formulalaryň dogry okalyşyny öwretmek. “Matematika–4” okuw kitabynda aňlatmalary, formulalary dogry okamaklyga ýardam edýän düşündirişler “M” şertli belgi bilen berilýär.

Meselem, “Deňsizlikleriň okalyşy:

a) 205 124- iki ýüz bäş uludyr bir ýüz ýigrimi dörtden; b) 79

2. Sözli ýazgydan belgili ýazga we tersine geçmäge degişli ýumuşlar ýerine ýetirmek.

Meselem, “Matematika–4” okuw kitabynda şeýle mysallar berilýär: «5000037000 san şeýle okalýar: „Bäş milliard otuz ýedi müň” ýa-da “Alty milliard elli üç müň dört” sany sifrler bilen şeýle ýazylýar: 6000053004».

3. Matematiki diktantlary geçirmek.

IV synpda matematiki diktantlaryň geçirilişi gollanmanyň 1.5. bölüminde berlendir.

4. Logiki gönükmeleri ýerine ýetirmek. Logiki gönükmeler okuw kitabynda “O” (oýunlar, gyzykly meseleler) şertli belgi bilen berilýär

5.Sözlemdäki galdyrylan sözleriň ornuna degişli sözleri ýazmaga degişli gönükmeleri ýerine ýetirmek.

Meselem, muňa mysal edip, “Matematika–4” okuw kitabyndaky 61-nji gönükmäni getirmek bolar: Galdyrylan sözleri ýazyň: 1) eger gyzyl galam gök galamdan 3 esse uzyn bolsa, onda gök galam gyzyl galamdan ...; 2) eger Myradyň sag elindäki taýajyklaryň sany çep elindäkiden 2 esse köp bolsa, onda onuň çep elindäki taýajyklaryň sany... 3) eger kakasy oglundan 3 esse agyr bolsa, onda ogly kakasyndan ...

6. Matematiki adalgalar bilen baglanyşykly oýunlary geçirmek. Şeýle oýunlaryň mazmuny şeýle: bir okuwçy haýsy bolsa-da bir adalgany (meselem, perimetr) aýdýar, ikinji okuwçy aýdylan adalganyň soňky harpy bilen başlanýan adalgany (meselem, radius) aýdýar we ş.m., kim degişli adalgany aýtmagy başarmasa, şol utulýar.

Oýun üçin gollanmanyň goşmaçasynda berlen adalgalary ulanyp bolar.

Mugallym matematiki adalgalaryň dogry aýdylmagyna, okuwçylaryň aýdýan sözlemleriniň grammatiki gurluşyna hemişe gözegçilik edip durmalydyr.

IV synpda matematika sapaklarynda interaktiw usulyň ulanylyşy

Okuwçylaryň döredijilik ukyplaryny ýüze çykarmakda we ösdürmekde okatmagyň interaktiw-özara hyzmatdaşlyk usulynyň, ýagny mugallymyň okuwçy, okuwçynyň okuwçy bilen hyzmatdaşlygynyň uly ähmiýeti bardyr. Okatmagyň bu usulynda okuwçylary sapaga köpçülikleýin çekmek bilen olaryň işjeňligi gazanylýar.

IV synpda matematika sapaklarynda okuwçylary toparlara bölmek bilen “Ýumuşlary özara çalyşmak” atly özara hyzmatdaşlyk usulynyň ulanylyşyna seredeliň.

Sapakda özara hyzmatdaşlygy ýola goýmak üçin synpyň okuwçylary iki, üç, dört, bäş, alty okuwçydan ybarat bolan toparlara bölünýär. Mugallym sapakdan öň topardaky okuwçylaryň sanyna görä öwrenilýän tema degişli ýumuşlary taýýarlaýar. Ýumuşlaryň her biri iki sany meňzeş meseleden ybarat edilip düzülýär.

Toparlarda ýumuşlaryň ikibara bolup ýerine ýetirilýändigi üçin, ilki bilen özara hyzmatdaşlykda ikibara bolup meseleleriň ýerine ýetirilişini görkezeliň.

IV synpda “Formula boýunça hasaplamak” atly tema degişli ýumuşlary aşakdaky görnüşde berip bolar:

1-nji ýumuş (M. 4, № 629)

a) 74 km/sag tizlik bilen 5 sagatda geçilen ýoly ýoluň formulasy boýunça tapyň.

b) 86 m/min tizlik bilen 35 minutda geçilen ýoly ýoluň formulasy boýunça tapyň.

2-nji ýumuş (M.4, № 630)

a) b=7, c=5 we r=4 bolsa, a=bc+r formula boýunça a bölünijini tapyň;

b) a=541, b=31 we с=17 bolsa, a=bс+r formula boýunça r galyndyny tapyň.

Okuwçylar ýumuşlary ýerine ýetirmäge girişýärler. O.Işanowa 1-nji, A.Poladowa bolsa 2-nji ýumuşyň meselelerini çözmek tabşyrylýar.

Mugallym 1 a) meseläniň çözülişini O.Işanowa 2 a) meseläniň çözülişini A.Poladowa düşündirýär. Soňra “Ýumuşlary özara çalyşmak” şeýle amala aşyrylýar: O.Işanow 1 a) meseläniň çözülişini A.Poladowa, A.Poladow bolsa 2 a) meseläniň çözülişini O.Işanowa öwredýär.

A.Poladow 1 b) meseläni, O.Işanow bolsa 2 b) meseläni özbaşdak çözmäge girişýärler. Olar biri-biriniň çözen meselelerini özara barlaýarlar. Şeýlelik bilen, ikibara bolup berlen ýumuşlary ýerine ýetirmek tamamlanýar.

Goý, synpyň okuwçylary alty-altydan toparlara bölünen bolsun. Mugallym tema degişli alty sany ýumuşy taýýarlaýar. Bu ýumuşlaryň her birinde iki sany birmeňzeş mesele berilýär. Toparlardaky okuwçylaryň her birine ýumuşlar paýlanyp berilýär. Berlen ýumuşlar tablisada nokat bilen bellik edilýär (1-nji tablisa)

1-nji tablisa.

Okuwçynyň familýasy, ady	1-nji ýumuş a), b)	2-nji ýumuş a), b)	3-nji ýumuş a), b)	4-nji ýumuş a), b)	5-nji ýumuş a), b)	6-njy ýumuş a), b)
Poladow A.	*
Işanow O.		*
Orazow Ç.			*
Saparow B.				*
Pälwanow S.					*
Kerimow S.						*

Mugallym okuwçylaryň her birine onuň ýumuşynyň a) meselesiniň çözülişini düşündirýär (wagty tygşytlamak üçin ýumuşlaryň a) meselesiniň gysga çözülişini öňünçä kagyza ýazyp, soňra olary okuwçylara bermek hem bolar).

Soňra okuwçylar öz ýumuşlaryndaky b) meseläni özbaşdak çözmäge girişýärler.

Öz ýumuşyndaky b) meseläni çözen okuwçy çözüşiniň dogrudygyny mugallymyň kömegi bilen barlaýar. Meseläni dogry çözenden soň, tablisada degişli ýerde + belgi goýulýar. Mysal üçin, Ç.Orazow 3-nji ýumuşyň b) meselesini dogry çözen bolsa, onuň familiýasynyň gabadyndaky nokada derek “+” belgi goýulýar. Käbir wagtdan soň tablisa aşakdaky görnüşi alar:

2-nji tablisa

Okuwçynyň familiýasy, ady	1-nji ýumuş a), b)	2-nji ýumuş a), b)	3-nji ýumuş a), b)	4-nji ýumuş a), b)	5-nji ýumuş a), b)	6-njy ýumuş a), b)
Poladow A.	+
Işanow O.		*
Orazow Ç.			+
Saparow B.				+
Pälwanow S.					+
Kerimow G.						*

Okuwçylar alan ýumuşlaryny çözenlerinden soň, galan ýumuşlary çözmek üçin olar ýokarda beýan edilişi ýaly ikibara bolup işleýärler.

2-nji tablisadan görnüşi ýaly, A.Poladow bilen Ç.Orazow bileleikde ýumuşlary özara çalyşyp işläp bilerler. Olara muny ýerine ýetirmek tabşyrylýar we tablisada A.Poladowyň gabadynda 3-nji ýumuşda nokat goýulýar, Ç.Orazowyň setirinde 1-nji ýumuşda nokat goýulýar. Şeýle etmek bilen B.Saparow bilen S.Pälwanow 4-nji we 5-nji ýumuşlary özara alyşýarlar. Jübütler işleri ýerine ýetirenden soň nokatlaryň ornuna “+” belgi goýulýar. Käbir wagtdan soň tablisa aşakdaky ýaly bolup biler:

3-nji tablisa

Okuwçynyň familiýasy, ady	1-nji ýumuş a), b)	2-nji ýumuş a), b)	3-nji ýumuş a), b)	4-nji ýumuş a), b)	5-nji ýumuş a), b)	6-njy ýumuş a), b)
Poladow A.	+		+
Işanow O.		+				*
Orazow Ç.	+		+
Saparow B.				+	+
Pälwanow S.				+	+
Kerimow G.		*				+

Ýumuşlary ýerine ýetirmek dowam etdirilýär: Poladow A. bilen Saparow B. 3-nji we 5-nji ýumuşlary Orazow Ç. bilen Pälwanow S. 1-nji we 4-nji ýumuşlary özara alyşýarlar. Işanow O. bilen Kerimow G. 2-nji we 6-njy ýumuşlary çözmegi dowam etdirilýärler. Şeýle etmek bilen okuwçylaryň her biri alty ýumuşy hem ýerine ýetirýärler (4-nji tablisa).

4-nji tablisa

Okuwçynyň familiýasy, ady	1-nji ýumuş a), b)	2-nji ýumuş a), b)	3-nji ýumuş a), b)	4-nji ýumuş a), b)	5-nji ýumuş a), b)	6-nji ýumuş a), b)
Poladow A.	+	+	+	+	+	+
Işanow O.	+	+	+	+	+	+
Orazow Ç.	+	+	+	+	+	+
Saparow B.	+	+	+	+	+	+
Pälwanow S.	+	+	+	+	+	+
Kerimow G.	+	+	+	+	+	+

Bu usul sapaklaryň hemmesinde hem ulanylyp bilner. Onuň üçin mugallym ýumuşlary okuw kitabyny, gollanmalary ulanyp öňünçä taýýarlamalydyr.

IV synpyň okuw maksatnamasynyň käbir temalaryna degişli interaktiw usuly ulanmak üçin taýýarlanylan ýumuşlary getireliň:

Tema: Deňleme we onuň çözülişi.

1-nji ýumuş. Deňlemäni çözüň:

a) x+37=85; b) y+156=218.

2-nji ýumuş. Deňlemäni çözüň:

a) 85-z=36; b) 2041-n=786.

3-nji ýumuş. Deňlemäni çözüň:

a) m-94=18; b) p-7698=2302.

4-nji ýumuş. Deňlemäni çözüň:

a) (x+15)-8=17; b) (24+x)-21=10.

5-nji ýumuş. Deňlemäni çözüň:

a) (45-y)+18=58; b) (y-35)+12=32.

6-njy ýumuş. Deňlemäni çözüň:

a) 56-(x-12)=24; b) 55-(x-15)=30.

Tema: Bölmegiň barlanylyşy.

1-nji ýumuş. Bölmegi köpeltmek bilen barlaň:

a) 11648:56; b) 7868:28.

2-nji ýumuş. Bölmegi bölmek bilen barlaň:

a) 684000: 1800; b) 8748:324.

3-nji ýumuş. Bölmegi köpeltmek we bölmek bilen barlaň:

a) 1176000:2100; b) 18291000:273.

4-nji ýumuş. Hasaplaň:

a) 20.(12:4); b) 240:(12:6 )

5-nji ýumuş. Hasaplaň:

a) (75.32.83):4 b) 19890: (13 .15.17).

6-njy ýumuş. Aňlatmanyň bahasyny tapyň:

a) eger a=98 bolsa, 3648+20678:a; b) eger b=42042 bolsa, 11986-b:7.

Tema: Köpeltmegiň paýlaşdyrma häsiýeti.

1-nji ýumuş. Aňlatmanyň bahasyny tapyň:

a) 69.27 +31.27; b) 917.49+49.23.

2-nji ýumuş. Aňlatmany köpeltmek hasyly görnüşinde ýazyň:

a) 23a + 37 a; b) 27p-17p.

3-nji ýumuş. Aňlatmanyň bahasyny tapyň:

a) a=238 bolanda 38a+62a; b) b=517 bolanda 375b-175b.

4-nji ýumuş. Deňlemäni çözüň:

a) 4x+4x=424; b) 15y-8y=714.

5-nji ýumuş. Aňlatmany ýönekeýleşdiriň:

a) 3a + 17+3a+14; b) k+35+4k+26.

6-njy ýumuş. Deňlemäni çözüň:

a) 4∙25 x=800; b) 5∙20 х =500.

Tema: Gönüburçlugyň meýdany

1-nji ýumuş.

a) Uzynlygy 5 sm., ini 2sm bolan gönüburçlugyň meýdanyny tapyň;

b) Ini 14 sm, uzynlygy 16 sm bolan gönüburçlugyň meýdanyny tapyň.

2-nji ýumuş.

a) Gönüburçluk görnüşli mellegiň meýdany 32m². Eger şol mellegiň ini 4 bolsa, onuň uzynlygyny tapyň.

b) Gönüburçluk görnüşli mellegiň meýdany 63m². Eger şol mellegiň uzynlygy 9m bolsa, onuň inini tapyň.

3-nji ýumuş.

a) Gönüburçluk görnüşli mellegiň uzynlygy 86m, onuň meýdany 3354m². Mellegiň inini tapyň.

Gönüburçluk görnüşli mellegiň ini 24 m, onuň meýdany 432m². Mellegiň uzynlygyny tapyň.

4-nji ýumuş.

a) Eger gönüburçlugyň perimetri 244 sm, ini 58 sm bolsa, onuň meýdanyny tapyň;

b) Eger gönüburçlugyň perimetri 100 sm, uzynlygy 32 sm bolsa, onuň meýdanyny tapyň.

5-nji ýumuş.

a) Eger s=81, b=3 bolsa, s=ab formulany ulanyp a-ny tapyň.

b) Eger a=12, s=72 bolsa, s=ab formulany ulanyp b-ni tapyň.

6-njy ýumuş.

a) Gönüburçluk görnüşli mellegiň uzynlygy 43m, ini bolsa uzynlygyndan 15m gysga. Mellegiň perimetrini we meýdanyny tapyň.

b) Gönüburçluk görnüşli mellegiň ini 12m, uzynlygy bolsa ininden 8 m uzyn. Mellegiň perimetrini we meýdanyny tapyň.

Multimediýa tehnologiýalaryny ulanyp “Ýumuşlary özara alyşmak” usulynda geçirilen sapagyň hem netijeli boljakdygy ikiuçsyzdyr. Multimediýa tehnologiýalary ýumuşlaryň

a) meselelerini okuwçylara düşündirmekde,

b) meseleleriň çözülişiniň dogrulygyny barlamakda, netijeleri tablisalarda görkezmekde örän peýdalydyr.

IV synpda matematikadan diktantlar

Matematikadan diktantlar okuwçylaryň bilim derejelerini barlamagyň bir görnüşidir. Matematika boýunça diktantda mugallymyň özi ýa-da ses ýazgysyny ulanyp okuwçylara sorag berýär. Okuwçylar berlen soraglara jogap ýazýarlar.

Matematikadan diktantyň bir wariantynyň geçirilişini nusga hökmünde getireliň.

Mugallym. «Natural sanlary deňeşdirmek» diýen temadan diktant.

Birinji ýumuş. Deňsizligi ýazyň: alty kiçidir sekizden. Gaýtalaýaryn. deňsizligi ýazyň: alty kiçidir sekizden.

Säginme (pauza)

Ikinji ýumuş: ..........

........................................

Bäşinji ýumuş. 11-den uly 13-den kiçi ähli natural sanlary ýazyň. Gaýtalaýaryn. 11-den uly 13-den kiçi ähli natural sanlary ýazyň.

Säginme.

Diktant gutardy.

Matematikadan diktantyň iki wariantda (birinji warianty oglanyň, ikinji warianty gyzyň okan ses ýazgysy) geçirilişi.

Oglanyň sesi. «Natural sanlary deňeşdirmek» diýen temadan diktant.

Birinji wariant. Birinji ýumuş. Deňsizligi ýazyň: Alty kiçidir sekizden. Gaýtalaýaryn. Alty kiçidir sekizden.

Gyzyň sesi. «Natural sanlary deňeşdirmek» diýen temadan diktant.

Ikinji wariant. Birinji ýumuş. Deňsizligi ýazyň: Dokuz uludyr ýediden. Gaýtalaýaryn. Dokuz uludyr ýediden.

Oglanyň sesi. Birinji wariant. Ikinji ýumuş. ...

Oglanyň sesi. Birinji wariant. Bäşinji ýumuş. 11-den uly 13-den kiçi ähli natural sanlary ýazyň. Gaýtalaýaryn. 11-den uly 13-den kiçi ähli natural sanlary ýazyň.

Gyzyň sesi. Ikinji wariant. Bäşinji ýumuş. 18-den kiçi 15-den uly ähli natural sanlary ýazyň. Gaýtalaýaryn. 18-den kiçi 15-den uly ähli natural sanlary ýazyň.

Säginme.

Oglanyň sesi. Diktant gutardy.

Matematikadan diktantlaryň nusgasy

1-nji diktant

Tema: Natural sanlar we nol. Natural sanlaryň okalyşy we ýazylyşy.

1. Zatlar sanalanda ulanylýan sanlara nähili sanlar diýilýär ? (476 sanda näçe onluk, näçe ýüzlük bar ?).

2. 3458 sanda näçe ýüzlük, näçe müňlük bar ? (Zatlar sanalanda ulanylýan sanlara nähili sanlar diýilýär ?).

3. 10 (0) san natural sanmy ?

4. Dört ýüz otuz bäş müň bäş (üç ýüz ýedi müň kyrk) sany sifrler bilen ýazyň.

5. Ýigrimi milliard ýüz million iki (otuz milliard üç ýüz million ýedi ýüz) sany sifrler bilen ýazyň.

6. Üçlük sifri we bäş sany noly (altylyk sifri we alty sany noly) ulanyp sany ýazyň.

7. Üçlük sifr we bäş sany nol (altylyk sifr we alty sany nol) ulanylyp ýazylan sanyň okalyşyny ýazyň.

2-nji diktant

Tema: Natural sanlary deňeşdirmek

1. Deňsizligi ýazyň: alty kiçidir sekizden (dokuz uludyr ýediden).

2. Deňsizligi ýazyň: 12 uludyr 10-dan (5 kiçidir 7-den).

3. 4815 we 4805 (6155 we 6555) sanlary deňeşdiriň.

4. «Kiçi» () belgini ulanmak bilen ýazyň: «12 kiçidir 19-dan» (25 uludyr 22-den).

5. 11-den uly 13-den kiçi (18-den kiçi 15-den uly) ähli natural sanlary ýazyň.

3-nji diktant

Tema: Natural sanlary goşmak we aýyrmak.

1. Sanlar goşulanda alynýan netijä näme diýilýär ? (Goşulýan sanlar nähili atlandyrylýar ?).

2. 3846 we 4154 (6768 we 3232) sanlaryň jemi näçä deň ?

3. 9464+0 (0+8001) jem näçä deň ?

4. 375 – 117 = 228 (483-239=244) deňligi ýazyň. Aýyrmagy goşmak bilen barlaň.

5. Eger х=4 bolsa 211–х (eger y=439 bolsa y–378) aňlatmanyň bahasyny tapyň.

6. Eger y=596 bolsa y–287 (eger х=7 bolsa 195–х) aňlatmanyň bahasyny tapyň.

7. х+72=95 (58+y=85) deňlemäni çözüň.

4-nji diktant

Tema: Natural sanlary köpeltmek.

1. 16 ∙ 4 (14 ∙ 3) köpeltmek hasylyny jem görnüşinde ýazyň.

2. 11+11+11 (10+10+10+10) jemi köpeltmek hasyly görnüşinde ýazyň.

3. 25-i (49-y) iki sany deň köpeldijiniň köpeltmek hasyly görnüşinde ýazyň.

4. Eger х=0 bolsa, 10х (eger y=1 bolsa 21y) aňlatmanyň bahasyny tapyň.

5. х-iň (y-iň) haýsy bahasynda 11х=11 (15у=0) deňlik dogry ?

6. Köpeltmegiň orun çalşyrma (utgaşdyrma) häsiýetini aňladýan deňligi ýazyň.

7. 15 we 146 (24 we 216) sanlaryň köpeltmek hasyly 2190-a (5184-e) deň.146 we 15 (216 we 24) sanlaryň köpeltmek hasyly näçä deň ?

8. Köpeltmegiň utgaşdyrma häsiýetini aňladýan deňligi ýazyň.

9. Amalyň amatly tertibini saýlap, hasaplamany ýerine ýetiriň:

4∙23∙42∙25 (50∙31∙6).

5-nji diktant

Tema: Natural sanlary bölmek.

1. х-iň (y-iň) haýsy bahasynda 14х=210 (18у=342) deňlik dogry ?

2. а:16=12 (252:в=12) deňlemäni çözüň.

3. 121:c=11 (m:13=13) deňlemäni çözüň.

4. 0:10 (0:20) aňlatmanyň bahasyny tapyň.

5. Eger bölüniji 505, bölüji 1 (bölüniji 343, bölüji 343) bolsa, paýy tapyň.

6. Eger bölüniji 185, bölüji 185 (bölüniji 309, bölüji 1) bolsa paýy tapyň.

7. Bölmegi ýerine ýetiriň: 462:22. Netijäni köpeltmek bilen barlaň. (Hiç bir sany... bölmek bolmaýar diýen sözlemi doly ýazyň).

8. Sözlemi doly ýazyň: «hiç bir sany... bölmek bolmaýar» (Bölmegi ýerine ýetiriň: 558:31. Netijäni köpeltmek bilen barlaň).

6-njy diktant

Tema: Kesim. Kesimiň uzynlygy.

1. Haýsy kesimler ABC (MKN) üçburçlugyň taraplary bolup hyzmat edýär ?

2. Dört (üç) kesimden ybarat döwük çyzygy çyzyň.

3. Dörtburçlugy çyzyň we ony A,B,C,D (M, N, K, E) harplar bilen belgiläň.

4. Ahyrky nokatlary A we B (C we D) bolan kesimleriň näçesini gurmak bolar?

5. Ahyrky nokatlary A we B (M we N) bolan kesimleriň belgilenişini ýazyň.

6. Haýsy nokatlar ABC (MNK) üçburçlugyň depeleri bolýandygyny ýazyň.

7. Uzynlygy 35 mm (15mm) bolan BC(MN) kesimleri guruň.

IV synpda matematikadan bäsleşikler we olaryň gecirilişi

Okuwçylaryň döredijilikli pikirlenmegini ösdürmekde bäsleşikleriň (olimpiýadalaryň) ähmiýeti uludyr. IV synpda geçirilýän bäsleşikler okuwçylaryň matematiki biliminiň giňelmegine we okuwçylary gyzykly meseleler bilen hem-de olaryň ajaýyp çözülişleri bilen tanyş etmäge ýardam edýär.

Matematikadan bäsleşigi guramaçylykly geçirmek mugallym üçin örän jogapkärli işdir.

Bäsleşige taýýarlyk we ony geçirmek üçin guramaçylyk topary döredilýär. Guramaçylyk toparyň başlygy edilip, mekdep müdiriniň okuw işleri baradaky orunbasary bellenilýär. Başlygyň orunbasary edilip, matematika dersi boýunça usuly birleşmäniň ýolbaşçysy bellenilýär.

Matematika mugallymlary we okuwçylar guramalarynyň wekilleri guramaçylyk toparynyň agzalarydyr.

Bäsleşige gatnaşan okuwçylaryň ýazuw işlerini barlamak we olara baha bermek üçin eminler bellenilýär. Eminleriň başlygy edip, matematika dersi boýunça usuly birleşmäniň ýolbaşçysy bellenýär.

Guramaçylyk toparynyň we eminleriň düzümi hem-de bäsleşigi geçirmegiň tertibi mekdep müdiriniň buýrugy bilen tassyklanylýar.

IV synpyň isleg bildiren okuwçylarynyň hemmesi bäsleşige gatnaşyp biler.

IV synpda bäsleşigiň dowamlylygy 90 minut bolmalydyr.

Bäsleşikde köplenç 4 sany mesele teklip edilýär.

Okuwçylar bäsleşikde teklip edilen meseleleri islendik tertipde ýerine ýetirip bilerler.

Bäsleşikde hödürlenilýän meseleler örän çylşyrymlydyklary boýunça sapaklarda çözülýän meselelerden has tapawutly bolsalar, onda bu ýagdaýyň okuwçylara ýaramaz täsir etmegi mümkindir. Bäsleşikde hödürlenýän meseleler sapakda çözülýän meselelere meňzeş bolup, olardan az tapawutlanýan bolsa, onda bu ýagdaý guýçli okuwlaryň bäsleşige sowuk-sala gatnaşmagyna elter. Şonuň üçin hem bäsleşigiň meselelerini taýýarlamaklyga örän jogapkärli çemeleşilmelidir.

Bäsleşige gatnaşan okuwçylaryň ýerine ýetiren ýumuşlarynyň her biri aşakdaky ýaly bahalandyrylyp bilner:

1) mesele dogry we doly çözülen bolsa, onda «+» (4 baha) goýulýar;

2) meseläniň çözülişiniň alnyp barlyşy dogry bolup, käbir kemçilikler bar bolsa, onda «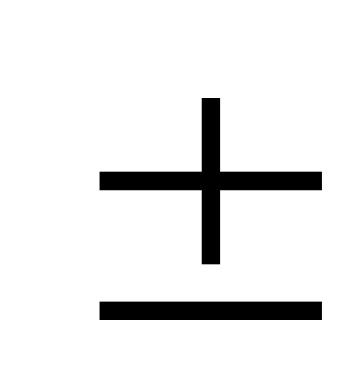 » (3 baha) goýulýar;

3) meseläniň çözüliş usuly tapylyp, ýöne ol ahyryna çenli dowam etdirilmedik bolsa, onda « » (2 baha) goýulýar;

4) meseläniň çözülişi gözlenip, dogry usuly tapylmadyk bolsa, onda «–» (1 baha) goýulýar;

5) mesele çözülmäge başlanmadyk bolsa, onda «0» (0 baha) goýulýar.

1-nji orny 11-12 baha, 2-nji orny 8-10 baha toplan okuwçy eýeleýär.

Mekdep müdiri, bäsleşigiň guramaçylyk topary we emin agzalary bilelikde bäsleşikde üstün çykan okuwçylary dabaraly ýagdaýda sylaglaýarlar.

IV synpda matematikadan bäsleşikler üçin

ýumuşlaryň nusgasy

1. 1-den 1000-e çenli natural sanlaryň jeminiň 143-e bölünýändigini subut ediň.

2. 8 kg noýba we çeküw daşsyz jamly terezi bar. Şol terezide 3 kg noýbany nähili çekip almaly ?

3. Jemi tapmaly: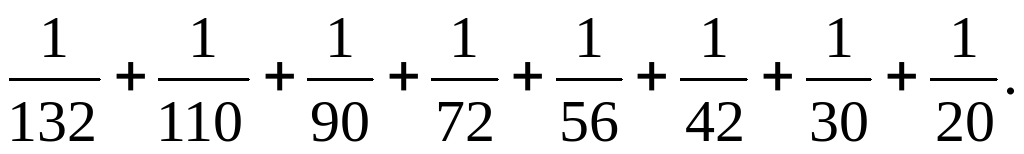

4. Läle duşenbe gününden başlap (bir hepdäniň içinde) öz kiçijik jigisine iki kitap okap berdi. Eger ol ikinji kitaby okap gutarmak üçin birinji kitaby okamaga sarp eden gününden 3 gün az sarp eden bolsa, birinji kitaby hepdäniň haýsy güni okap gutarypdyr ?

Ýumuşlaryň çözülişi:

1. Ilkinji 1000 natural sanlaryň jemini şeýle görnüşde ýazalyň: 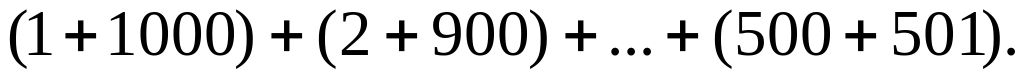Bu jemiň goşulyşylarynyň her biri 1001-e deň. 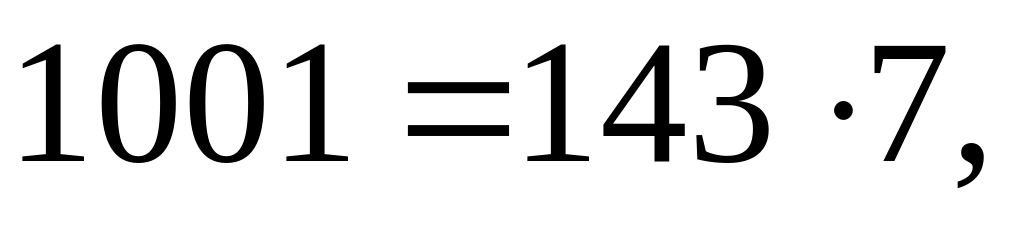diýmek, ähli jem 143-e bölünýär.

2. Bölüp 4 kg çekip almaly, 4 kg-y bölüp, 2 kg çekip almaly, ony ýene bölüp 1kg çekip almaly.

3. Berlen droblaryň her birini iki drobuň tapawudy görnüşinde ýazalyň, mysal üçin, 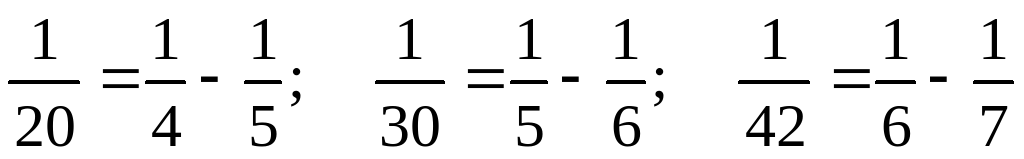. we ş.m. Jogaby:

4. Ikinji kitaby okamak üçin 2 gün, birinjini okamak üçin 5 gün sarp bolupdyr. (2+5=7). Kitabyň okalyp başlanan güni – duşenbe, bäşinji gün bolsa annadyr. Ikinji kitaby şenbe güni bilen ýekşenbe güni okapdyrlar, diýmek, birinji kitaby anna güni okap gutarypdyrlar.

«Matematika–4» okuw kitabyndaky halkara adalgalarynyň gelip çykyşy barada maglumatlar

Okuwçylara temalary öwretmekde döwrebaplyk hem-de ylmylyk ýörelgelerine eýerilip matematikanyň mekdep kursuna halkara adalgalaryň birnäçesi girizilendir.

Halkara adalgalarynyň gelip çykyşy we many-mazmuny bilen okuwçylaryň tanyşdyrylmagy, olaryň matematika bolan gyzyklanmalaryny ösdürjekdigi ikuçsyzdyr.

«Matematika, 4» okuw kitabyndaky halkara adalgalarynyň gelip çykyşy baradaky gysgaça maglumatlary getireliň.

Bissektrisa – latyn bi (iki) sectriх (bölüji) diýen sözlerden emele gelen. Ol iki deň bölýän diýmegi aňladýar.

Gradus – latyn gradus sözi bolup, ädim, basgançak diýmekdir.

Gram – fransuz gramm sözünden gelip çykan, agyrlygyň kiçi ölçegi.

Desimetr – latyn decem-on we grek metreo-ölçeýärin diýen sözlerden gelip, metriň ondan bir ülşi diýmegi aňladýar.

Diagonal – grek dia üstünden we gonia burç diýen sözleriniň utgaşmagyndan alnyp, burçdan burça gidýän diýmegi aňladýar.

Kwadrat – latyn guadratus sözünden alnyp, dörtburçly diýmegi aňladýar.

Koordinata – co bilelikde we ordinatus tertipleşdirmek diýen latyn sözlerinden emele gelip, tertipleşdirilen diýmegi aňladýar.

Kub – kubos diýen grek sözi bolup, oýnalýan süňk diýmegi aňladýar.

Krossword – iňlis cross-atanak, kesişmek we word-söz diýen sözlerinden gelip çykan.

Kilometr – grek kilo – müň we metreo-ölçeýärin sözlerinden gelip çykan. Müň metr diýmegi aňladýar.

Kilogram – fransuz kilo-müň we grek gramma kiçi agyrlyk ölçegi diýen sözlerden gelip çykyp, müň gram diýmekdir.

Litr – grek litra sözünden gelip çykan. Sygym ölçegi.

Natural – naturalis diýen latyn sözünden gelip çykyp, hakyky, tebigy diýen manyny berýär.

Nol – hiç zat diýmegi aňladýan latyn nullus diýen sözden gelip çykýar. Latyn diline araplaryň sifr boş sözünden, arap diline bolsa hindileriň sinia boşluk diýen sözünden geçendir.

Parallellepiped – parallelos – ýanaşyk ýöremek, epipedon – tekizlik diýen grek sözlerinden gelip çykýar.

Perimetr – grekleriň peri-töwerek, daş-töwerek, metreo ölçeýärin diýen sözlerinden gelip çykyp, daş-töweregi ölçeýärin diýmegi aňladýar.

Proporsiýa – praportio diýen latyn sözünden gelip çykyp, ölçegdeş diýmekdir.

Radius – şöhle, tigriň simi diýmegi aňladýan radius diýen latyn sözünden gelip çykyp, tigriň merkezinden onuň töweregine geçirilip birikdirilen taýajyklar diýmegi aňladýar.

Sirkul – latyn circulus – töwerek diýen sözden gelip çykýar

Sifr – arap sifr boş diýen sözi emele getirýär.

Santimetr – fransuz cent – ýüz we grek metreo – ölçeýärin diýen sözlerden gelip çykyp, metriň ýüzden bir ülşi diýmegi aňladýar.

Sentrner – latyn centum (ýüz) diýen sözden gelip çykan.

Transportir – latynça transportare – geçirýärin diýen sözden gelip çykýar.

Tonna – latyn tonna (boçka, gap) sözünden gelip çykan, massa birliginiň ady.

Million – fransuz million – müň sany müň diýen sözden gelip çykan.

Milliard – fransuz milliard – müň sany million diýen sözden gelip çykan.

Millimetr – grek milli – müň we metro – ölçeýärin, diýen sözden gelip çykyp, metriň müňden bir ülşi diýmegi aňladýar.

Metr – grek sözi metreo – ölçeýärin diýmegi aňladýar.

Milli gram – latyn milli – müň we grek gramma – kiçi agyrlyk ölçegi diýen sözlerden gelip çykyp, gramyň müňden bir ülşi diýmegi aňladýar.

Figura – latynça figura sözi bolup, daşky görnüş diýen manyny berýär.

Formula – kesgitli düzgün diýen latyn sözünden gelip çykandyr.

«Matematika-4» okuw kitabyndaky belgileriň gelip çykyşy barada maglumatlar

2007-2008-nji okuw ýylyndan başlap ýurdumyzyň orta mekdeplerinde matematika dersi Tükmenistanyň Milli bilim institutynyň ylmy işgärleri, ýokary we orta mekdepleriň mugallymlary tarapyndan taýýarlanylan täze okuw kitaplary boýunça okadylýar. Bu okuw kitaplaryna täze düşünjeler we olara degişli belgiler hem girizilendir. Okuw kitaplaryna girizilen şol belgileri şertli iki topara bölüp bolar.

Birinji topara ýazgysy degişli düşünjäni aýdyň görkezýän «Δ» (üçburçluk), «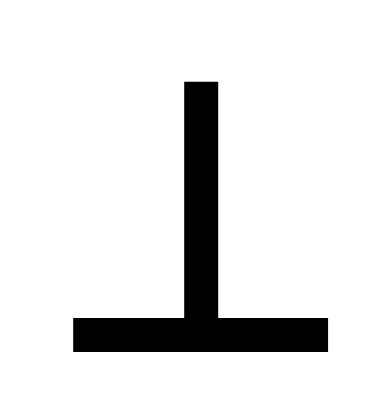 » (perpendikulýar), «||» (papallel) ýaly belgiler, ikinji topara bolsa, düşünjäniň manysyny gyýtaklaýyn aňladýan «%» (göterim), « » (kök), «∫» (integral) ýaly belgiler degişlidir.

Birinji topara degişli belgilere düşünmeklik okuwçylarda kynçylyk döretmeýär, ýöne ikinji toparyň belgilerine welin okuwçylaryň gowy düşünmekleri üçin ol belgileriň gelip çykyşy, many-mazmuny düşündirilmelidir.

Okuw kitaplarynda matematikanyň belgileriniň gelip çykyşyna degişli maglumatlaryň ýeterlik däldigi sebäpli IV synpda matematika dersinde ulanylýan belgilere degişli maglumatlary getirýäris.

«º» (gradus belgisi). Grek matematigi Ptolomeý töweregiň üç ýüz altmyşdan

bir bölegini belgilemek üçin «töweregiň bölegi» diýmegi aňladýan «μoiρα»

sözüni ulanypdyr. Bu söz soňra ilkinji iki harpy ulanylyp «μ°» görnüşde

ýazylypdyr. Wagtyň geçmegi bilen gysgalyk üçin «μ°» ýazga derek «°» belgi

ulanylypdyr.

(burç belgisi) burçuň kiçeldilen görnüşidir, ony 1634-nji ýylda fransuz

matematigi P.Erigon girizipdir. 1971-nji ýylda akademik A.M.Kolmogorow

burçuň ululygy üçin « ^ » belgini girizdi.

« + » (goşmak) belgi, goşmak amalyny we položitel ululygy belgilemek üçin

ulanylýar. Bu belginiň gelip çykyşyny söwda bilen hem baglanyşdyrýarlar:

gapdaky suwuklygyň satylan bölegini çyzyjak (-) bilen belläpdirler.

Suwuklygyň satylan bölegi doldurylandan soň, öňki çyzyjygyň üstünden

çyzypdyrlar (+).

« – » (aýyrmak) belgi aýyrmak amalyny we otrisatel ululygy belgilemek üçin

ulanylýar. « + » we « – » belgiler ХV asyryň italýan alymy Leonardo da

Winçiniň we nemes matematigi Widmanyň işlerinde ulanylýar.

« = » (deňlik) belgi iňlis matematigi R.Rikord tarapyndan 1557-nji ýylda

girizilipdir.

( ) (ýaýlar) belgi ХVI asyr italýan matematikleriniň işinde duş gelýär.

« ∙ » (köpeltmek) belgini 1691-nji ýylda iňlis alymy U.Outred, « х » (köpeltmek)

belgini 1698-nji ýylda nemes matematigi G.Leýbnis ulanypdyr.

« ׃ » (bölmek) belgini G.Leýbnis 1684-nji ýylda ulanypdyr.

« » (uly), «(kiçi) belgiler 1631-nji ýylda iňlis matematigi G.Harriota

tarapyndan girizilipdir.

a², a³, a⁴, … belgiler ilkinji gezek fransuz alymy Rene Dekartyň 1637-nji

ýylda çap edilen işlerinde duş gelýär.

aⁿ belgini 1676-njy ýylda iňlis alymy Isaak Nýuton teklip edipdir.

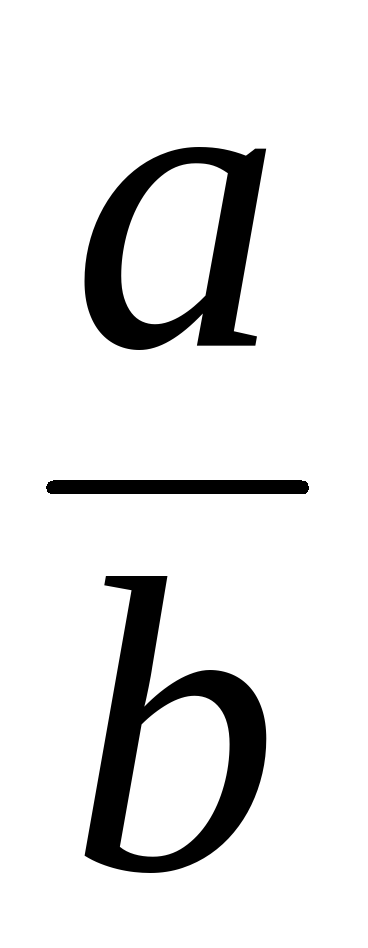belgi droby belgilemek üçin 1202-nji ýylda italýan alymy Fibonaççi

tarapyndan ulanylypdyr.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sifrler, şeýle hem latyn we grek elipbiýiniň harplary

matematiki belgiler hökmünde ulanylýar. Matematikada latyn uly A, B, С…

harplary bilen nokatlar, köplükler, kiçi setir a, b, с… harplary bilen bolsa göni

çyzyklar, üçburçlugyň, köpburçlugyň taraplary belgilenýär.

S - «meýdan» diýen iňlis «Square» sözüniň birinji harpydyr.

V - «göwrüm» diýen fransuz «Volume» sözüniň birinji harpydyr.

T - «ýyly» diýen latyn «Temperatura» sözüniň birinji harpydyr.

t - «wagt» diýen iňlis «taým» sözüniň birinji harpydyr.

υ - «tizlik» diýen fransuz «υaleur» sözüniň birinji harpydyr.

Bellik.Materiallar şu okuw kitaby boýunça taýýarlanyldy: G.Şadurdyýew, A.Öwezow, H.Geldiýew. Matematika. Orta mekdepleriň IV synpy üçin okuw kitaby. Aşgabat, Türkmen döwlet neşirýat gullugy, 2004.

15