ПЛАН УРОКА
Урок №___
Предмет: математика
Дата проведения_20.04.2020_
Преподаватель: Амирханова А. К.
Группа № __1-2_
Специальность: 36.01.01 Младший ветеринарный вельдшер.
Тема урока: Перпендикуляр и наклонная. Теорема о трех перпендикулярах
Ни для кого не секрет что вся элементарная геометрия пришла к нам в основном с Египта и Греции. В далекие и древние времена геометрия использовалась как наука для измерения земли, а также очень тесно при строительстве. Все теоремы, законы и аксиомы выводили и доказывали, чтобы облегчить измерительные или строительные работы. Сегодняшняя тема была очень важна для людей того времени так как перпендикуляр и наклонная основные ориентиры при работе такого типа.
-
При пересечении прямые образуют четыре угла.
-
Углом между пересекающими прямыми является больший из двух смежных углов.
-
Две прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом.
-
Через произвольную точку прямой в пространстве можно провести перпендикулярную ей прямую.
-
Если две пересекающиеся прямые параллельны двум перпендикулярным прямым, то они тоже параллельны.
-
Через любую точку пространства, не принадлежащую прямой, нельзя провести прямую, перпендикулярную данной.
-
Если прямая, перпендикулярна одной из двух параллельных прямых и лежит с ними в одной плоскости, то она параллельна и второй прямой.
-
Вопросы нахождение перпендикулярных прямых и плоскостей по кубу.
Повторить теорему Пифагора.
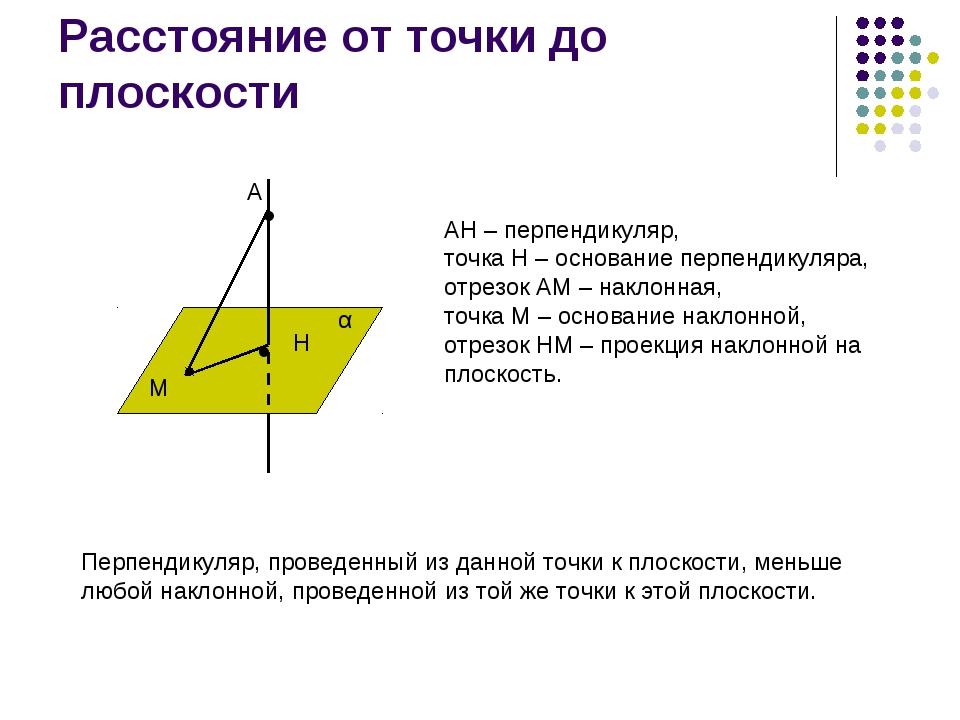
Пусть точка A не принадлежит плоскости α . Проведем прямую a, проходящую через эту точку и перпендикулярную α . Точку пересечения прямой a с плоскостью α обозначим O. Отрезок AO называется перпендикуляром, опущенным из точки A на плоскость α.
Наклонной к плоскости называется прямая, пересекающая эту плоскость и не перпендикулярная ей. Наклонной называют также отрезок, соединяющий точку, не принадлежащую плоскости, с точкой плоскости, и не являющийся перпендикуляром.
На рисунке: АО – перпендикуляр к плоскости α, АВ – наклонная, ОВ – проекция наклонной.
Примеры материальных моделей перпендикуляров к плоскости: столб, телевизионная вышка перпендикулярны плоскости горизонта; перпендикулярно этой плоскости забивают сваи, бурят скважины, проходят шахтные стволы, запускают космические корабли. Только набрав нужную высоту, ракета отклоняется в нужном направлении.
Введение понятия расстояния от данной точки до плоскости.
Из всех расстояний от точки А до различных точек плоскости α наименьшим является расстояние до точки В. Это расстояние, т.е. длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.
Теорема о перпендикуляре и наклонной
Перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из той же точки к той же плоскости.
Доказательство. Пусть AB – наклонная к плоскости α, AO – перпендикуляр, опущенный на эту плоскость. Соединим отрезком точки O и B. Треугольник AOB прямоугольный, AB гипотенуза, AO – катет. Следовательно, AO AB.
Теорема о трех перпендикулярах
Д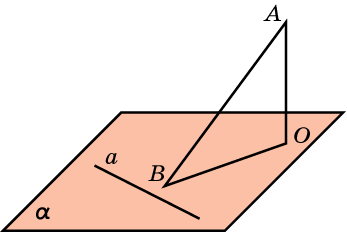 оказательство.
оказательство.
Пусть прямая а плоскости α перпендикулярна проекции OB наклонной АВ. Тогда она будет перпендикулярна двум пересекающимся прямым OB и AO. По признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости АOВ и, следовательно, она будет перпендикулярна наклонной АВ.
5. Закрепление нового материала.
1. Верно ли утверждение: «Если из двух различных точек, не принадлежащих плоскости, проведены к ней две равные наклонные, то их проекции тоже равны»?
Ответ: Нет.
2. К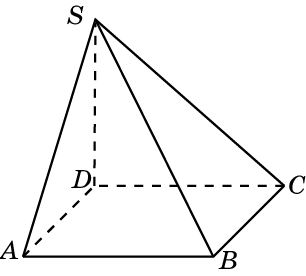 плоскости прямоугольника ABCD в точке пересечения диагоналей восстановлен перпендикуляр. Верно ли утверждение о том, что произвольная точка M этого перпендикуляра равноудалена от вершин прямоугольника?
плоскости прямоугольника ABCD в точке пересечения диагоналей восстановлен перпендикуляр. Верно ли утверждение о том, что произвольная точка M этого перпендикуляра равноудалена от вершин прямоугольника?
Ответ: Да
3. Точка M равноудалена от всех точек окружности. Верно ли утверждение о том, что она принадлежит перпендикуляру к плоскости окружности, проведённому через её центр?
Ответ: Да
4. Основание ABCD пирамиды SABCD – прямоугольник, AB BC. Ребро SD перпендикулярно плоскости основания. Среди отрезков SA, SB, SC и SD укажите наименьший и наибольший.
Ответ: SD – наименьший; SB – наибольший.
Задачи:
1) Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C. Найдите отрезок AC, если AB = 6 см, ÐBAC = 60°.(Ответ 12 см)
2) Отрезки двух наклонных, проведенных из одной точки к плоскости, равны 15 см и 20 см. Проекция одного из этих отрезков равна 16 см. Найдите проекцию другого отрезка.(Ответ 9 см)
3) Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C. Найдите проекцию отрезка AC, если AC = 37 см, AB = 35 см.(Ответ 12 см)
Решить № 5.42.
. Самостоятельная работа.
1. Какой отрезок называется перпендикуляром?
2. Какой отрезок называется наклонной?
3. Какой отрезок называется проекцией наклонной?
4. Какая точка называется основанием перпендикуляра?
5. Какая точка называется основанием наклонной?
6. Что называется расстоянием от данной точки до плоскости?
7. Как найти расстояние от точки до плоскости?
8. Может ли наклонная быть короче перпендикуляра, проведенного из той же точки?
9. Если наклонные, проведённые из одной точки к плоскости равны, то что можно сказать об их проекциях?
10. Как сформулировать обратное утверждение?
11. Точка А не лежит на плоскости . Сколько наклонных одной длины можно провести из этой точки к данной плоскости?
. Сколько наклонных одной длины можно провести из этой точки к данной плоскости?
12. Если точка равноудалена от всех вершин прямоугольника, то во что она проектируется на его плоскость?
| № п/п | Вопрос | Варианты ответа | Ответ |
| 1 (1 балл) | Как называется линия, соединяющая основания перпендикуляра и наклонной? | а) отрезок; б) угол; в) проекция; г) расстояние. | |
| 2 (1 балл) | Прямая проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и... | а) самой себе; б) самой наклонной; в) самой проекции; г) самому перпендикуляру. | |
| 3 (1 балл) | Расстояние от точки до прямой равно длине... | а) наклонной; б) медианы; в) проекции; г)перпендикуляра | |
| 4 (1 балл) | Из двух наклонных, исходящих из одной точки, не лежащей на данной плоскости, больше та, у которой... | а)перпендикуляр больше; б) проекция меньше; в) проекция больше; г) перпендикуляр меньше. | |
| 7 (2 балла) | Точка А не лежит в плоскости, а точка Е - принадлежит этой плоскости. АЕ = 13, проекция этого отрезка на плоскость равна 5. Каково расстояние от точки А до данной плоскости? | а) 144; б) 8; в) 18; г) 12. | |
Жду ваши ответы и вопросы на адрес электронной почты asiyat.karimullaevna@yandex.ru







 оказательство.
оказательство. плоскости прямоугольника ABCD в точке пересечения диагоналей восстановлен перпендикуляр. Верно ли утверждение о том, что произвольная точка M этого перпендикуляра равноудалена от вершин прямоугольника?
плоскости прямоугольника ABCD в точке пересечения диагоналей восстановлен перпендикуляр. Верно ли утверждение о том, что произвольная точка M этого перпендикуляра равноудалена от вершин прямоугольника? 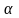 . Сколько наклонных одной длины можно провести из этой точки к данной плоскости?
. Сколько наклонных одной длины можно провести из этой точки к данной плоскости?


















