«Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства». Бертран Рассел
Математика – царица наук, тесным образом перекликается с музыкой. Несомненно, математика пронизывает музыку.
Музыка и ее первый звук родились одновременно с творением мира, как утверждали древние мудрецы.
В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера “Диссертация о звуке”, написанная в 1727 году: “Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков”.
Свое отношение к математике и музыки ученые высказывались в своих личных переписках. Так, к примеру, Лейбниц в письме Гольдбаху пишет: “Музыка есть скрытое арифметическое упражнение души, не умеющей считать”. На что Гольдбах ему отвечает: “Музыка – это проявление скрытой математики”.
Однако, одним из первых, кто попытался выразить красоту музыки с помощью чисел, был Пифагор. Он создал свою школу мудрости, положив в ее основу два предмета – музыку и математику. Музыка, как одно из видов искусств, воспринималась наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.
Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он был не только философом, но и математиком, и теоретиком музыки. Родился Пифагор около 570 года до нашей эры на острове Самосее. Пифагор основал науку о гармонии сфер, утвердив ее, как точную науку. Известно, что пифагорейцы пользовались специальными мелодиями против ярости и гнева. Они проводили занятия математикой под музыку, так как заметили, что она благотворно влияет на интеллект. Он учился музыки в Египте и сделал ее предметом науки в Италии. Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга.
Одним из достижений Пифагора и его последователей в математической теории музыки был разработанный ими «Пифагоров строй». Новая технология использовалась для настройки популярного в то время инструмента – лиры. Тем не менее, «Пифагоров строй» был несовершенен, как и древнегреческая арифметика. Расстояние между соседними звуками «Пифагорова строя» неодинаковые. Он – неравномерный. Чтобы сыграть мелодию, от какой- либо другой ноты, лиру каждый раз нужно перенастраивать. Исследованию музыки посвящали свои работы многие величайшие математики, такие как: Рене Декарт ( его первый труд - “Compendium Musicae” в переводе “Трактат о музыке” ) , Готфрид Лейбниц, Христиан Гольдбах, Жан Д’Аламбер, Даниил Бернулли и другие.
«Раздумывая об искусстве и науке, об их взаимосвязях и противоречиях, можно сделать вывод, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая и духовная деятельность человека. Что между ними размещается все, что человечество создало в области наук и искусства» – писал Г. Нейгауз. Изучив работы ученых,можно установить, что в прошлом были неоднократные попытки рассматривать музыку, как один из объектов изучения математики.
Таким образом, многие учёные в древности считали, что гармония чисел является сродни гармонии звуков и дополняет друг друга, музыку и математику.
Исследования музыкальных произведений
Произведение Г. Гладкова «Бременские музыканты»
Попробуем сделать математическую модель этого произведения: каждой ноте мы присвоили номер ступени. Цифра 1 – I ступень, 2 – II ,3 – III, 4 – IV, 5 – V ,6 – VI ,7 – VII, 8 – I, 9 – II ,0 – III.
Переложили ноты на числа и получили при этом такой ряд чисел:
11123313 / 535 / 44432246 / 545 / 3353 / 666716 / 22217572 / 176 / 4561 / 7672 / 321117 / 176213 / 444443 / 22221 /.
Черта между цифрами служит тактовой четой, то есть делит их на такты, так как сделано в произведении.
В музыке есть понятие – устойчивые ступени, на которых строится тоническое трезвучие (Т5/3): 1, 3, 5 ступени.
Если в каждом полном такте сложить номера устойчивых ступеней, то мы заметим следующую закономерность.
В первом такте сумма равна 13 (1+1+1+3+3+1+3), во II – тоже 13 (5+5+3), в III – 3 (3), в IV – 10 (5+5), в V – 14 (3+3+5+3), в VI – 1, в VII – 6 (5+1), в VIII – 1, в IX – 6 (5+1), в X – 0, в XI – 6 (3+1+1+1), в XII – 4 (1+3), в XIII – 3, в XIV – 1.
Получили ряд чисел: 13, 13, 3, 10, 14, 1, 6, 1, 6, 0, 6, 4, 3, 1.
Вывод: Следовательно, наблюдаем, что в произведении повторяется группа цифр: 14, 13, 10, 6, 4, 3 ,1, 0.
Теперь попробуем перемножить в каждом такте номера ступеней.
Получили числа в соответствии с номерами тактов:
I. 54 (1*1*1*2*3*3*1*3).
II. 75 (5*3*5)
III. 18432 (4*4*4*3*2*2*4*6)
IV.100 (5*4*5)
V. 135 (3*3*5*x3)
VI. 9072 (6*6*6*7*1*6)
VII. 3920 (2*2*2*1*7*5*7*2)
VIII. 12 (1*7*6)
IX. 120 (4*5*6*1)
X. 288 (7*6*7*2)
XI. 336 (3*2*2*2*2*7)
XII. 252 (1*7*6*2*1*3)
XIII. 3072 (4*4*4*4*4*3)
XIV. 16 (2*2*2*2*1)
Имеем следующий ряд чисел: значения в I (11123313) и II (535); III (44432246) и XIII (444443); VI (666716), VIII (176) и XIV (22221); XI (322227), IX (4561) и VII (22217572) тактах получились разные за счет того, что количество нот в них различное.
Классическое произведение И. С. Баха Хорошо темперированный клавир «Прелюдия №1»
Рассмотрим шесть тактов этого произведения.
Получили следующий ряд чисел:
1351351313513513 / 1262462412624624 / 7252452472524524 / 1351351313513513 / 1263663613636636 / 1262462412624624 /…
Сложим цифры – устойчивые ступени.I – 44, II – 2, III – 20, IV – 44, V – 17, VI – 2…
Получили ряд чисел: 44, 2, 20, 44, 17, 2.
Следовательно, наблюдаем, что в произведении повторяется группа цифр: 44 и 2.
Теперь попробуем перемножить в каждом такте номера ступеней.
Получили числа в соответствии с номерами тактов:
I. 455625 (1*3*5*1*3*5*1*3*1*3*5*1*3*5*1*3)
II. 21233664 (1*2*6*2*4*6x2x4x1x2x6x2x4x6x2x4)
III. 501760000 (7x2x5x2x4x5x2x4x7x2x5x2x4x5x2x4)
IV. 455625 (1x3x5x1x3x5x1x3x1x3x5x1x3x5x1x3)
V. 136948896 (1x2x6x3x6x6x3x6x1x3x6x3x6x6x3x6)
VI. 21233664 (1x2x6x2x4x6x2x4x1x2x6x2x4x6x2x4)
Числа I и IV, II и VI тактов повторяются, следовательно представляют математическую модель, которая имеет числовую закономерность.
Любое музыкальное произведение можно представить как математическую модель, которая будет иметь числовые закономерности. Однако, в ходе выполнения исследования, выше перечисленными способами, мною выявлено, что каждый числовой ряд имеет свою математическую закономерность ( из-за разного количества нот в тактах).
Таким примером является музыкальное произведение «Бременские музыканты».
Просмотр содержимого документа
«Математика и музыка. Гармония математических пропорций в музыке.»

Гармония математических пропорций в музыке

Математика и музыка - два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.

Первым, кто изучил связь
музыки и математики был великий древнегреческий ученый Пифагор.
В Древней Греции развивалась музыкальная теория и музыкальная эстетика. Пифагор и пифагорейцы научно сформулировали ряд акустических законов музыки. Пифагор поднял искусство до истинно достойного состояния, продемонстрировав его математические основания.

Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства ее должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы. Необходимую, существенную связь музыки и числа обнаружили, как известно, еще пифагорейцы, которые, открыв числовые соотношения, лежащие в основе музыкальных созвучий, явились, собственно говоря, родоначальниками музыкальной теории. Пифагор создал свою школу мудрости, положив в ее основу два искусства – музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга.

В музыке звуки , расположены подряд, от нижнего до верхнего, напоминают лестницу в многоэтажном доме. Обычная лестница делится на пролеты, наша звуковая - тоже. В каждом пролете звуковой лестницы семь ступеней(клавиш), а с восьмой начинается уже следующий пролет.
Вот эта лесенка на клавишах рояля (пианино).
(8)
7
6
5
4
3
2
1
ми
до
соль
фа
си
ля
до
ре

В основе теории о связи музыки и математики лежит интервал . А в музыке интервал - это расстояние между двумя звуками, которое измеряется тонами и полутонами. Существуют основные интервалы между звуками. Эти интервалы получили свои названия: прима терция квинта септима
секунда кварта секста октава

В каждом интервале используется определенное количество ступеней, необходимое для его построения. Само же название интервалов произошло от названия цифр, обозначающих количество ступеней этого интервала по-латыни: прима – один
секунда – два
терция – три
кварта – четыре
квинта – пять
секста – шесть
септима – семь
октава - восемь
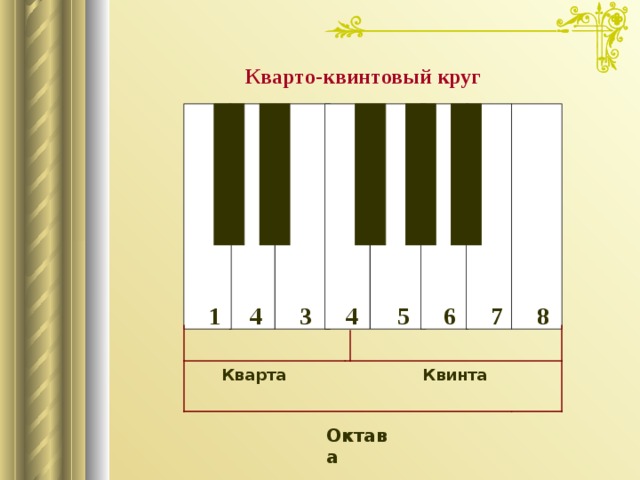
Кварто-квинтовый круг
3
5
6
7
1
4
4
8
Квинта
Кварта
Октава
ля
до
си
соль
фа
до
ми
ре
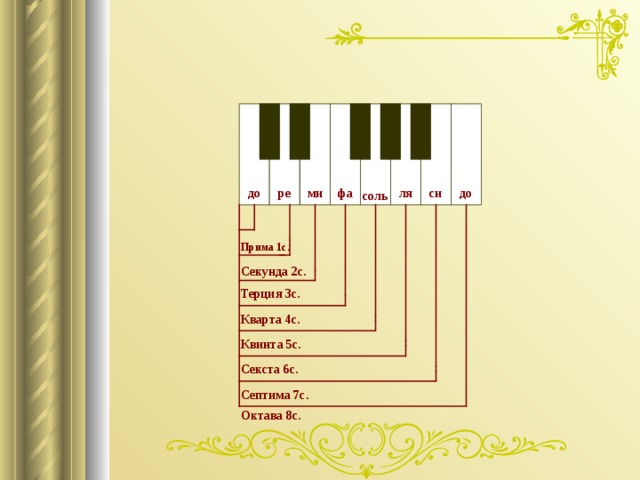
Прима 1с .
Секунда 2с.
Терция 3с.
Кварта 4с.
Квинта 5с.
Секста 6с.
Септима 7с.
Октава 8с.

Эти интервалы являются консонансами, т.е мягкими , ласкающими слух. Они широко используются в музыкальной практике до сих пор. Именно на них строятся мелодии.
На протяжении многих столетий музыканты настраивали инструменты так, как это делали в Древней Греции, основываясь на наших интервалах.

Длительность нот
Гармония математических пропорций в музыке прослеживается и на примере длительностей нот.
Целую ноту делят пополам в результате образуется половинная нота, т.е. 1/2 от целой ноты. Половинные в свою очередь делят еще на половины, образуются четвертные ноты, т.е. 1/4 от целой или 1/2 от половинной. Четвертные ноты делятся на восьмые, а те на шестнадцатые и т.д.
Продолжительность звучания всех нот зависит от продолжительности звучания целой ноты, которая считается на четыре счета.

Схема деления целой ноты
Целая 1
Половинная 1/2
Четвертная 1/4
Восьмая 1/8
Шестнадцатая 1/16

У школьников обычно складывается впечатление, что математика занимается исключительно числами и измерениями. Однако, на самом деле, математика – это нечто гораздо большее, чем просто наука для счетоводов и кассиров. Математика и музыка : сегодня эти две великие сферы культуры многими воспринимаются как два полюса или даже как две противоборствующие духовные силы, тогда как на самом деле они тесно переплетены крепкими незримыми узами.
Но прежде, чем в науке утвердилось новое учение о числе , прежде , чем появился новый музыкальный строй, прошла целая эпоха.

Спасибо за внимание































