Математика и туризм (геометрия на службе у туриста)

Математика и туризм: геометрия на службе у туриста

г. Петрозаводск

Республика Карелия

Рулева Т.Г.

• Значение геометрии

• Знание геометрии и умение применять эти знания на практике полезно в любой профессии.
• В школе мы подробно изучаем геометрические построения с помощью циркуля и линейки и решаем много задач. А как решить такие же задачи на местности?
• Такие знания бывают довольно часто нужны и в других областях деятельности.

Рулева Т.Г.

Расстояние до недоступной точки

Немного истории:

Фалес Милетский

Рулева Т.Г.

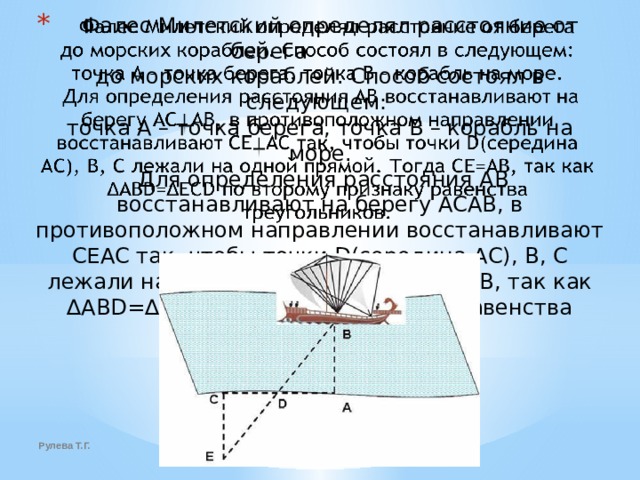
Фалес Милетский определял расстояние от берега

до морских кораблей. Способ состоял в следующем:

точка А – точка берега, точка В – корабль на море.

Для определения расстояния AB восстанавливают на берегу ACAB, в противоположном направлении восстанавливают CEAC так, чтобы точки D(середина АС), B, C лежали на одной прямой. Тогда CE=AB, так как ∆ABD=∆ECD по второму признаку равенства треугольников.

Рулева Т.Г.

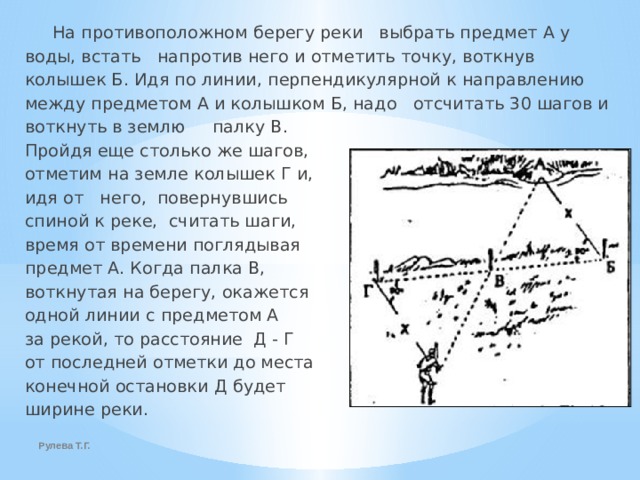
На противоположном берегу реки выбрать предмет А у воды, встать напротив него и отметить точку, воткнув колышек Б. Идя по линии, перпендикулярной к направлению между предметом А и колышком Б, надо отсчитать 30 шагов и воткнуть в землю палку В. Пройдя еще столько же шагов, отметим на земле колышек Г и, идя от него, повернувшись спиной к реке, считать шаги, время от времени поглядывая на предмет А. Когда палка В, воткнутая на берегу, окажется на одной линии с предметом А за рекой, то расстояние Д - Г от последней отметки до места конечной остановки Д будет равно ширине реки.

Рулева Т.Г.

Определение расстояния построением подобных треугольников

Определение расстояния с помощью спички.

Спичка - простейший дальномер.

Предварительно на ней надо нанести чернилами или карандашом двухмиллиметровые деления. Необходимо также знать примерную высоту предмета, до которого определяется расстояние. Так, рост человека в метрах равен 1,7, колесо велосипеда имеет высоту 0,75, всадник - 2,2, телеграфный столб - 6, одноэтажный дом без крыши - 2,5 - 4 метра. Пусть, надо определить расстояние до телеграфного столба. Направляем на него спичку на вытянутой руке , длина которой у взрослого человека равна приблизительно 60 см. На спичке изображение столба заняло два деления, то есть 4 миллиметра. На этих данных нетрудно составить такую пропорцию: длина руки / расстояние до столба = отрезок спички / высота столба = 0,60/Х = 0,004 / 6,0; Х=0,60*6,0/0,004=900 Таким образом, до столба 900 метров.

Рулева Т.Г.

• Геометрия в произведениях литературы

Рулева Т.Г.

Жюль Верн «Таинственный остров»

Герои Жюля Верна измеряли высоту скалы. Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены.

«- если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены».

«0ба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее - 500 футам. По окончании  измерений инженер составил следующую запись: 15:500 = 10:х, 500×10 = 5000, 5000:15 = 333,3. Значит, высота  гранитной  стены равнялась   333 футам».

Рулева Т.Г.

Артур Конан-Дойль

«Обряд дома Месгрейвов»

Определение высоты дерева.

    «Я связал вместе два удилища, что дало мне шесть футов, и мы с моим клиентом отправились обратно к тому месту, где рос (когда-то) вяз... Я воткнул свой шест в землю, отметил направление тени и измерил ее. В ней было девять футов. Дальнейшие мои вычисления были совсем уж несложны. Если палка высотой шесть футов отбрасывает тень в девять футов, то дерево (вяз)  высотой (64 фута) отбросит тень в (96 футов), и направление той и другой, разумеется, будет совпадать».

9

96

6

64

Рулева Т.Г.

Измерение высоты дерева

Рулева Т.Г.

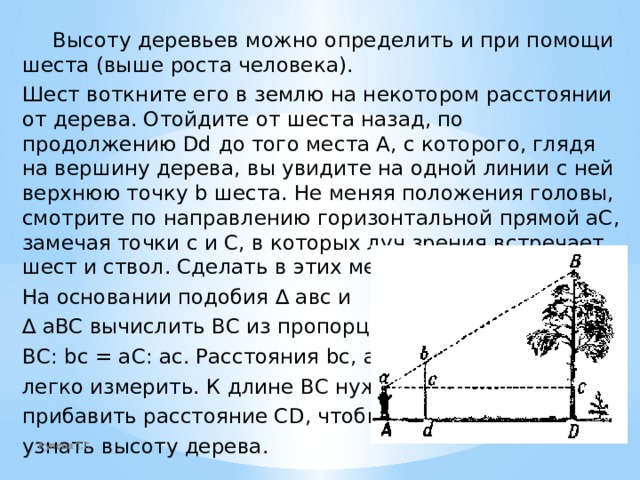
Высоту деревьев можно определить и при помощи шеста (выше роста человека).

Шест воткните его в землю на некотором расстоянии от дерева. Отойдите от шеста назад, по продолжению Dd до того места А, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку b шеста. Не меняя положения головы, смотрите по направлению горизонтальной прямой aC, замечая точки с и С, в которых луч зрения встречает шест и ствол. Сделать в этих местах пометки.

На основании подобия ∆ авс и

∆ aBC вычислить ВС из пропорции

ВС: bc = aC: ас. Расстояния bc, aC

легко измерить. К длине ВС нужно

прибавить расстояние CD, чтобы

узнать высоту дерева.

Рулева Т.Г.

«Крест дровосека»

Надо приставить одну палочку концом к переносице, расположив её параллельно земле. Вторую палочку надо приставить вертикально к дальнему концу первой.

Получится буква Т, лежащая «на боку». Отступая от дерева или приближаясь к нему, надо добиться того, чтобы верхушка и подножие дерева совпали с верхним и нижним концами вертикальной палочки. Расстояние от места, где стоит измеряющий, до подножия дерева равно высоте дерева.

Рулева Т.Г.

Измерение с зеркалом

На землю положить зеркало. Измеряющий отходит от зеркала на такое расстояние, чтобы увидеть в нем отражение верхушки дерева. Угол падения равен углу отражения. ∆ABO ∞ ∆CDO. CD= *OD. Расстояния OB и OD можно измерить, а AB = росту измеряющего – 8-10см.

Рулева Т.Г.

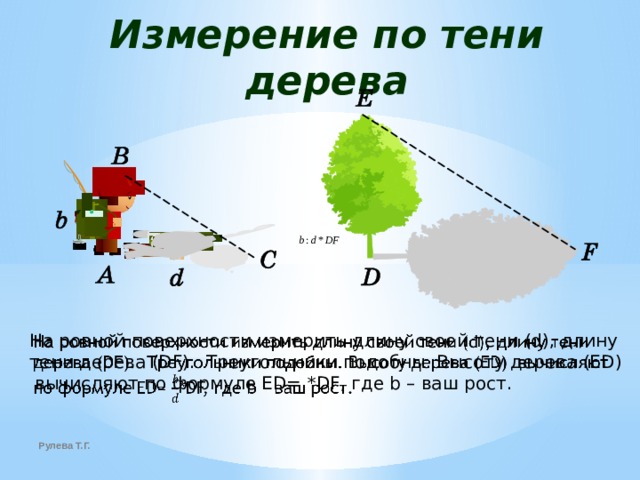
Измерение по тени дерева

На ровной поверхности измерить длину своей тени (d), длину тени дерева (DF). Треугольники подобны. Высоту дерева (ED) вычисляют по формуле ED= *DF, где b – ваш рост.

Рулева Т.Г.

• Построение окружности по трем данным точкам

Рулева Т.Г.

• Пусть три группы туристов расположены в пунктах А, В, С, не лежащие на одной прямой. Для проведения общего костра турфирме надо выбрать место, равноудаленное от этих групп. Как это можно сделать?

• Соединим эти точки отрезками АВ и ВС.  Чтобы найти точки равноудалённые от точек А и В проведем серединный перпендикуляр к АВ. Чтобы найти точки, равноудалённые от точек В и С, проведем серединный перпендикуляр к ВС.  Точка О - точка пересечения этих перпендикуляров будет равноудалена от данных точек А, В и С. Точка О служит центром окружности, проходящей через три точки А, В и С, не лежащие на одной прямой.
• Задача имеет единственное решение.
• Значит, в пункте О можно организовать общий костер для трех групп туристов.

Рулева Т.Г.

• Заключение

• В данной презентации рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями на местности – измерением расстояния до недоступной точки, измерением высоты предмета.

Используемые источники:

1.Балк М.Б., Балк Г.Д. «Математика после уроков», М., Просвещение, 1971.

2.Депман И.Я., Виленкин Н.Я. «За страницами учебника математики», М., Просвещение, 1989.

3.Карпушина Н.М. «Любимые книги глазами математика», М., Наука и жизнь, 2011.

4.Козлова Ю. «Математика на туристической тропе» – Математика, №16, 2011 г.

5.Сергеев И.Н., Олехник С.Н., Гашков С.Б. «Примени математику», М., Наука, 1989.

Рулева Т.Г.