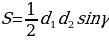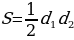Вторая часть ОГЭ по математике
Содержание:
Часть 2: назначение, критерии оценивания заданий. Распределение заданий части 2 по проверяемым умениям и способам деятельности. Задания по алгебре. Задания по геометрии.
Часть 2: назначение, критерии оценивания заданий
Задания части 2 ОГЭ по математике направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленных обучающихся, составляющих потенциальный контингент профильных классов.
Задания части 2 направлены на проверку таких качеств математической подготовки выпускников, как:
уверенное владение формально-оперативным алгебраическим аппаратом;
умение решить комплексную задачу, включающую в себя знания из разных тем курса алгебры;
умение решить планиметрическую задачу, применяя различные теоретические знания курса геометрии;
умение математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования;
владение широким спектром приёмов и способов рассуждений.
Часть 2 содержит задания повышенного и высокого уровней сложности из различных разделов математики. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Каждое из заданий части 2 оценивается в 2 балла.
Задания, ответы на которые оцениваются в 2 балла, считаются выполненными верно, если экзаменуемый выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае учащемуся выставляется максимальный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику экзамена выставляется 1 балл.
Важно обратить внимание учеников, что система оценивания задач с развёрнутыми ответами предполагает возможность их решения разными способами, а также привлечение математических фактов, приведённых в школьных учебниках, без необходимости их доказательств.
Распределение заданий части 2 по проверяемым умениям и способам деятельности
Распределение заданий части 2 по разделам кодификатора требований к уровню подготовки выпускников представлено в таблицах 1 и 2.
Распределение заданий части 2 по разделам КЭС представлено в таблице 1.
Таблица 1. Распределение заданий части 2 по разделам содержания курса математики
| Код по КЭС | Название раздела | Количество заданий |
| 3 | Уравнения и неравенства | 2 |
| 5 | Функции и графики | 1 |
| 7 | Геометрия | 3 |
Таблица 2. Распределение заданий части 2 по проверяемым умениям и способам действий
| Код по КТ | Основные умения и способы действий | Количество заданий |
| 3 | Уметь решать уравнения, неравенства и их системы | 1 |
| 4 | Уметь строить и читать графики функций | 1 |
| 5 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 2 |
| 7.3 | Моделировать реальные ситуации на языке алгебры; составлять выражения, уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры | 1 |
| 7.8 | Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | 1 |
Задания по алгебре
Задание 20 ОГЭ по математике открывает блок заданий повышенного и высокого уровней сложности и представляет собой алгебраическую задачу по одной из трёх следующих тем: «Преобразование рациональных выражений», «Уравнения и системы уравнений», «Неравенства».
Для решения уравнений (а именно они составляют самую значительную часть заданий 20 банка ОГЭ по математике), как и в более простых заданиях с кратким ответом, используются метод введения новой переменной, разложение на множители, условие равенства степеней и другие стандартные приёмы.
Как правило, в данном задании требуется решить уравнение степени больше двух – это может быть биквадратное или кубическое уравнение.
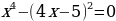
Алгоритм решения:
Определить тип уравнения.
Перенести правую часть уравнения в левую.
Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
Разложить на множители.
Приравнять каждый множитель к нулю
Решить полученные уравнения.
Записать ответ.
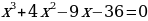
Алгоритм решения:
Определить тип уравнения.
Найти делители свободного члена уравнения.
Определить среди делителей один из корней.
Выполнить деление кубического многочлена на выражение (х-а), где а – найденный корень.
Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
Решить уравнение.
Записать ответ.
Задание 21 представляет собой традиционную текстовую задачу по одной из трёх тем: «Движение», «Производительность и работа», «Проценты и концентрация». Некоторые из этих задач можно решить арифметически, не прибегая к составлению уравнению, другие требуют составления одного или двух уравнений и их решения.
Задание 22 ОГЭ по математике представляет собой задачу по теме «Графики функций». Это задание можно отнести к относительно сложным, но следует понимать, что сложность эта относительна и в данном случае обусловлена либо формулой, задающей функцию и предполагающей предварительные алгебраические преобразования для получения одной из базовых функций школьного курса (из области определения которой в некоторых случаях придётся исключить одну или две точки), либо самим условием, требующим исследования взаимного расположения графиков двух функций и ответа на определённые вопросы о числе их общих точек в зависимости от некоторой величины.
Задания по геометрии
Напомним основные факты школьного курса геометрии, связанные с треугольниками:
сумма углов треугольника равна 180°;
внешний угол треугольника равен сумме двух не смежных с ним внутренних углов треугольника;
высоты треугольника пересекаются в одной точке;
биссектрисы треугольника пересекаются в одной точке (эта точка является центром вписанной в треугольник окружности);
серединные перпендикуляры к сторонам треугольника пересекаются в одной точке (эта точка является центром описанной около треугольника окружности);
медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин треугольника;
средняя линия треугольника параллельна одной из его сторон и равна её половине.
В равнобедренном треугольнике углы при основании равны, а высота, проведённая к основанию, является медианой и биссектрисой, поэтому на ней и находятся центры вписанной и описанной окружностей.
Частный случай равнобедренного треугольника - равносторонний треугольник. В нём каждая высота является медианой и биссектрисой, поэтому центры вписанной и описанной окружностей совпадают и R = 2r.
Среди всех треугольников особое место занимает прямоугольный треугольник. В прямоугольном треугольнике один из катетов можно считать высотой, а другой – основанием. Поэтому площадь прямоугольного треугольника равна половине произведения катетов. Разумеется, все остальные формулы площади треугольника применимы и к прямоугольному треугольнику. Кроме того, для прямоугольного треугольника справедлива теорема Пифагора, а синус, косинус или тангенс его острого угла можно найти как отношение катета к гипотенузе или катета к катету.
Таким образом, для прямоугольного треугольника справедливы следующие основные формулы: 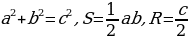
Приведём основные факты по теме «Окружность и круг»:
центральный угол окружности измеряется дугой окружности, на которую он опирается;
вписанный угол окружности равен половине центрального угла и измеряется половиной дуги, на которую он опирается;
касательная к окружности перпендикулярна радиусу этой окружности, проведённому в точку касания;
отрезки касательных, проведённых к окружности из одной точки, равны;
центр окружности, вписанной в угол, лежит на биссектрисе этого угла;
длина окружности равна 2πr, где r - радиус окружности;
площадь круга равна πr2, где r - радиус круга.
Напомним основные факты об углах, связанных с окружностью, и о взаимном расположении окружностей:
угол между двумя секущими к окружности, пересекающимися внутри окружности, равен полусумме дуг, высекаемых на окружности любой из пар вертикальных углов, образованных этими секущими;
угол между двумя секущими к окружности, пересекающимися вне окружности, равен полуразности дуг, высекаемых на окружности любой из пар вертикальных углов, образованных этими секущими;
касательная к окружности перпендикулярна её радиусу, проведённому в точку касания;
отрезки касательных, проведённых к окружности из одной точки, равны;
центр окружности, вписанной в угол, лежит на биссектрисе этого угла;
две окружности не имеют общих точек в том и только том случае, если расстояние между их центрами больше суммы радиусов этих окружностей;
две окружности имеют ровно две общие точки (пересекаются в двух точках) в том и только том случае, если расстояние между их центрами меньше суммы радиусов этих окружностей;
две окружности имеют ровно одну общую точку (касаются) в том и только том случае, если расстояние между их центрами равно сумме радиусов этих окружностей.
Напомним свойства и теоремы, связанные с четырёхугольниками, изучаемые в основной школе.
Сначала приведём основные факты, связанные c параллелограммом:
противоположные стороны параллелограмма параллельны и равны;
сумма двух углов параллелограмма, прилежащих к одной из его сторон, равна 180°;
диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Пусть a и b - длины двух смежных сторон параллелограмма, 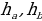 - соответственно высоты, проведённые к этим сторонам, γ - угол между этими сторонами, S - площадь параллелограмма. Основные формулы для вычисления площади параллелограмма: S = aha = bhb; S = absinγ.
- соответственно высоты, проведённые к этим сторонам, γ - угол между этими сторонами, S - площадь параллелограмма. Основные формулы для вычисления площади параллелограмма: S = aha = bhb; S = absinγ.
Кроме того, для параллелограмма, разумеется, справедлива и формула площади произвольного выпуклого четырёхугольника: если d1 и d2 - длины диагоналей выпуклого четырёхугольника, γ - угол между ними, то площадь S этого четырёхугольника равна полупроизведению диагоналей четырёхугольника на синус угла между ними, то есть: 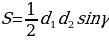
Важнейшими частными случаями параллелограмма являются прямоугольник, ромб, квадрат. Они обладают всеми свойствами параллелограмма, но для них справедливы и некоторые дополнительные свойства, которыми произвольные параллелограммы не обладают:
диагонали прямоугольника (а значит, и квадрата) равны;
диагонали ромба (а значит, и квадрата) взаимно перпендикулярны.
Площадь S прямоугольника равна произведению двух его смежных сторон a и b, т. e. S = ab. Площадь квадрата S равна квадрату его стороны а, то есть S = a2. Для вычисления площадей прямоугольника и ромба можно использовать формулу площади выпуклого четырёхугольника. Поскольку диагонали d1 и d2 ромба взаимно перпендикулярны, из формулы следует, что площадь ромба равна полупроизведению его диагоналей: 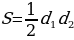
He в каждый параллелограмм можно вписать окружность, и не для каждого параллелограмма существует описанная окружность. Описать окружность можно только около прямоугольника (и, следовательно, квадрата); её центром будет точка пересечения диагоналей прямоугольника. Вписать окружность можно только в ромб (и, следовательно, в квадрат); её центром будет точка пересечения диагоналей ромба.
Трапеция является более сложным четырёхугольником по сравнению с параллелограммом, поскольку у неё параллельны только две стороны (основания трапеции), а две другие не параллельны (боковые стороны трапеции). Трапеция, у которой одна из боковых сторон перпендикулярна основаниям, называется прямоугольной. Трапеция, боковые стороны которой равны, называется равнобедренной (диагонали такой трапеции равны, углы при любом из оснований также равны). Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Задание 23 ОГЭ по математике открывает условный блок из трёх геометрических задач с развёрнутым решением, традиционно представленных в качестве трёх последних заданий ОГЭ по математике.
Это планиметрическая задача на вычисление, для решения которой нужно достаточно свободно ориентироваться в материале школьного курса планиметрии, в его теоремах, связанных с треугольниками, многоугольниками (преимущественно параллелограммами и трапециями) и окружностями.
Задание 24 представляет собой планиметрическую задачу на доказательство, связанную со свойствами треугольников, четырёхугольников, окружностей. Во многих случаях доказательство может быть проведено несколькими способами.
Завершающее задание 25 ОГЭ по математике представляет собой планиметрическую задачу на вычисление, более сложную по сравнению с заданием 23. Задание 23 можно рассматривать как своего рода подготовительную задачу: многие идеи и методы, необходимые для её решения, используются и при решении задания 25. Значительная часть задач связана с окружностью.
Литература:
Спецификация КИМ для проведения в 2021 году ОГЭ по математике, подготовленная ФГБНУ «ФИПИ».
Демонстрационный вариант КИМ для проведения в 2021 году ОГЭ по математике, подготовленная ФГБНУ «ФИПИ».
Кодификатор проверяемых требований к результатам освоения основной образовательной программы основного общего образования и элементов содержания для проведения ОГЭ по математике, подготовленная ФГБНУ «ФИПИ».
ОГЭ 2020. Математика. Основной государственный экзамен. Тематические экзаменационные задания / Ю.А. Глазков, И.К. Варшавский, М.Я. Гаиашвили. – М.: издательство «Экзамен», 2020.
Математика. Основной государственный экзамен. Готовимся к итоговой аттестации / А.В. Семёнов, А.С. Трепалин, И.В. Ященко, П.И. Захаров, И.Р. Высоцкий, Л.А. Титова. – М.: издательство «Интеллект-центр», 2020.
Ященко И.В., Шестаков С.А. Математика. Подготовка к основному государственному экзамену ОГЭ по математике 2018.
Колягин Ю.М. и др. Изучение алгебры в 7-9 классах. Книга для учителя.
https://spadilo.ru/oge-po-matematike/
https://math-oge.sdamgia.ru/
7







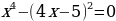
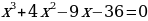
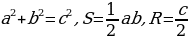
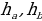 - соответственно высоты, проведённые к этим сторонам, γ - угол между этими сторонами, S - площадь параллелограмма. Основные формулы для вычисления площади параллелограмма: S = aha = bhb; S = absinγ.
- соответственно высоты, проведённые к этим сторонам, γ - угол между этими сторонами, S - площадь параллелограмма. Основные формулы для вычисления площади параллелограмма: S = aha = bhb; S = absinγ.