Окружностью называется множество точек, расположенных на одинаковом расстоянии от данной точки, которая называется центром окружности.
Для любой точки  , лежащей на окружности выполняется равенство
, лежащей на окружности выполняется равенство  ( Длина отрезка
( Длина отрезка  равна радиусу окружности.
равна радиусу окружности.
Отрезок, соединяющий две точки окружности называется хордой.
Хорда, проходящая через центр окружности называется диаметром окружности ( ).
). 

Длина окружности:

Площадь круга:

Дуга окружности:
Часть окружности, заключенная между двумя ее точками называется дугой окружности. Две точки окружности определяют две дуги. Хорда  стягивает две дуги:
стягивает две дуги:  и
и  . Равные хорды стягивают равные дуги.
. Равные хорды стягивают равные дуги.

Угол между двумя радиусами называется центральным углом:
 Чтобы найти длину дуги
Чтобы найти длину дуги  , составляем пропорцию:
, составляем пропорцию:
а) угол  дан в градусах:
дан в градусах:


Отсюда 
б) угол  дан в радианах:
дан в радианах:


Отсюда 
Диаметр, перпендикулярный хорде, делит эту хорду и дуги, которые она стягивает пополам:

Если хорды 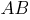 и
и  окружности пересекаются в точке
окружности пересекаются в точке 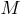 , то произведения отрезков хорд, на которые они делятся точкой
, то произведения отрезков хорд, на которые они делятся точкой 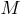 равны между собой:
равны между собой:


Касательная к окружности.
Прямая, имеющая с окружностью одну общую точку называется касательной к окружности. Прямая, имеющая с окружностью две общие точки называется секущей.
Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке:


Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть:


Следствие: произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть:


Углы в окружности.
Градусная мера центрального угла равна градусной мере дуги, на которую он опирается:

∠ ⌣
⌣ 
Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписанным углом. Вписанный угол измеряется половиной дуги, на которую он опирается:
 ∠
∠ ∠
∠
Вписанный угол, опирающийся на диаметр, прямой:

∠ ∠
∠ ∠
∠
Вписанные углы, опирающиеся на одну дугу, равны:

∠ ∠
∠ ∠
∠
Вписанные углы, опирающиеся на одну хорду равны или их сумма равна 
 ∠
∠ ∠
∠
∠ ∠
∠ ∠
∠
Вершины треугольников с заданным основанием и равными углами при вершине лежат на одной окружности:

Угол между двумя хордами (угол с вершиной внутри окружности) равен полусумме угловых величин дуг окружности, заключенных внутри данного угла и внутри вертикального угла.
 ∠
∠ ∠
∠ ∠
∠ ( ⌣
( ⌣  ⌣
⌣  )
)
Угол между двумя секущими (угол с вершиной вне окружности) равен полуразности угловых величин дуг окружности, заключенных внутри угла.

∠ ∠
∠ ∠
∠ ( ⌣
( ⌣  ⌣
⌣  )
)
Вписанная окружность.
Окружность называется вписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.
 Не во всякий многоугольник можно вписать окружность.
Не во всякий многоугольник можно вписать окружность.
Площадь многоугольника, в который вписана окружность можно найти по формуле
 ,
,
здесь  - полупериметр многоугольника,
- полупериметр многоугольника,  - радиус вписанной окружности.
- радиус вписанной окружности.
Отсюда радиус вписанной окружности равен 
Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:


В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.
 Радиус вписанной окружности равен
Радиус вписанной окружности равен  . Здесь
. Здесь 
Описанная окружность.
Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:
Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна  .
.

∠ +∠
+∠ =∠
=∠ +∠
+∠
Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:
 Радиус описанной окружности вычисляется по формулам:
Радиус описанной окружности вычисляется по формулам:


Где  - длины сторон треугольника,
- длины сторон треугольника,  - его площадь.
- его площадь.
Теорема Птолемея
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:








 , лежащей на окружности выполняется равенство
, лежащей на окружности выполняется равенство  ( Длина отрезка
( Длина отрезка  равна радиусу окружности.
равна радиусу окружности. ).
). 



 стягивает две дуги:
стягивает две дуги:  и
и  . Равные хорды стягивают равные дуги.
. Равные хорды стягивают равные дуги.
 Чтобы найти длину дуги
Чтобы найти длину дуги  дан в градусах:
дан в градусах:






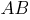 и
и 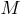 , то произведения отрезков хорд, на которые они делятся точкой
, то произведения отрезков хорд, на которые они делятся точкой 








 ⌣
⌣ 
 ∠
∠ ∠
∠

 ∠
∠ ∠
∠

 ∠
∠ ∠
∠

 ∠
∠ ∠
∠

 ∠
∠ ∠
∠ ∠
∠ ( ⌣
( ⌣  ⌣
⌣  )
)
 ∠
∠ ∠
∠ ( ⌣
( ⌣  ⌣
⌣  Не во всякий многоугольник можно вписать окружность.
Не во всякий многоугольник можно вписать окружность. ,
, - полупериметр многоугольника,
- полупериметр многоугольника,  - радиус вписанной окружности.
- радиус вписанной окружности.


 Радиус вписанной окружности равен
Радиус вписанной окружности равен 

 +∠
+∠ =∠
=∠ +∠
+∠
 Радиус описанной окружности вычисляется по формулам:
Радиус описанной окружности вычисляется по формулам:

 - длины сторон треугольника,
- длины сторон треугольника,  - его площадь.
- его площадь.











