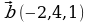Просмотр содержимого документа
«Математика СТ-21 01.11.2021»
Векторное произведение двух векторов
Пусть 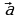 ,
, 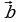 и
и 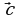 три ненулевые вектора, не параллельные одной плоскости. Приводя их к общему началу получим систему трех векторов.
три ненулевые вектора, не параллельные одной плоскости. Приводя их к общему началу получим систему трех векторов.
С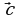 истема трех векторов
истема трех векторов 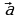 ,
, 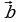 ,
, 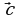 называется правой, если поворот вектора
называется правой, если поворот вектора
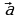 , совмещающий его по кратчайшему пути с вектором
, совмещающий его по кратчайшему пути с вектором 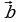 совершается против часовой стрелки для наблюдателя, глаз которого помещается в конце вектора
совершается против часовой стрелки для наблюдателя, глаз которого помещается в конце вектора 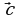 .
.
Если же упомянутый поворот совершается по часовой стрелке, то система векторов 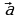 ,
, 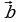 ,
, 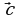 называется левой.
называется левой.
Имеет значение в каком порядке взяты векторы.
Векторным произведением вектора 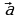 на не коллинеарный с ним вектор
на не коллинеарный с ним вектор 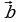 называется вектор
называется вектор 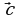 , который строится следующим образом:
, который строится следующим образом:
1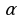 ) его модуль численно равен площади параллелограмма (
) его модуль численно равен площади параллелограмма (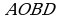 ), построенного на векторах
), построенного на векторах 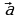 и
и 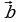 , т.е. он равен
, т.е. он равен 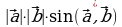
2) его направление перпендикулярно к плоскости указанного параллелограмма
3) при этом направление вектора 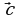 выбирается так (из двух возможных), чтобы векторы
выбирается так (из двух возможных), чтобы векторы 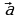 ,
, 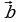 ,
, 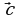 составляли правую систему.
составляли правую систему.
Обозначение: 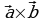
Свойства векторного произведения:
1. При перестановке сомножителей векторное произведение меняет знак на обратный, т.е. 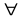 векторов
векторов 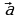 и
и 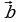 имеет место следующее соотношение
имеет место следующее соотношение 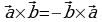
2.  векторов
векторов 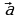 ,
, 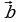 и
и 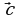 имеет место следующее соотношение
имеет место следующее соотношение 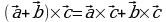
3. 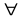 векторов
векторов 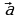 и
и 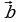 и числа α имеет место следующее соотношение
и числа α имеет место следующее соотношение 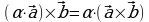
Если векторы 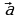 и
и 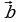 заданы своими координатами
заданы своими координатами 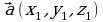 и
и 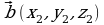 , то векторное произведение находится по формуле
, то векторное произведение находится по формуле 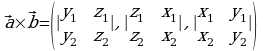
Задание: Найти векторное произведение векторов 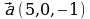 и
и 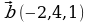







 ,
, 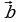 и
и 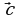 три ненулевые вектора, не параллельные одной плоскости. Приводя их к общему началу получим систему трех векторов.
три ненулевые вектора, не параллельные одной плоскости. Приводя их к общему началу получим систему трех векторов.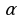 ) его модуль численно равен площади параллелограмма (
) его модуль численно равен площади параллелограмма (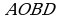 ), построенного на векторах
), построенного на векторах 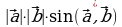
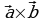
 векторов
векторов 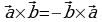
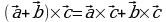
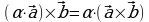
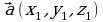 и
и 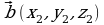 , то векторное произведение находится по формуле
, то векторное произведение находится по формуле 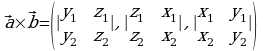
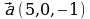 и
и