МАТЕМАТИКА ДЛЯ СТРОИТЕЛЕЙ

Учебно-методическое пособие для студентов
Введение
Велика роль задач в профессиональной направленности математической подготовки обучающихся строительных специальностей. Задачи выступают основным средством формирования качеств личности, необходимых для выполнения основных видов профессиональной деятельности. Переходя к понятию профессионально ориентированной задачи в строительстве, заметим, что в качестве задачной ситуации в ней выступает некая модель профессиональной ситуации, в которой по известным характеристикам профессионального объекта или явления надо найти другие его характеристики или свойства. Разрешение или исследование представленной профессиональной ситуации способствует развитию у обучающихся определенных профессиональных качеств, профессиональному развитию личности обучающегося. Умение решать такие задачи является необходимым условием успешного формирования будущего специалиста - строителя.
Основной целью создания пособия является оказание методической помощи обучающимся при решении профессионально-ориентированных задач как на занятиях математики так и при решении профессиональных задач строительного содержания при изучении специальных дисциплин по профилю.
Пособие состоит из теоретической части, которая располагается на первых страницах. В ней даны основные математические формулы, которые могут понадобиться при решении.
В данной разработке все задачи разделены на четыре основных вида:
1) задачи, в которой в математической модели требуется применить формулы объемов геометрических тел;
2) задачи, в которых для решения необходимо применит формулу площади боковой или полной поверхности геометрического тела;
3) задачи, в которых требуются умения вычислять площади плоских фигур и сторон прямоугольного треугольника;
4) задачи, в которых рассматриваются комбинации геометрических тел.
Для знакомства с основными идеями решения предлагаемых задач каждого вида приводятся примеры задач с подробным решением. Каждый пример сопровождается блоком задач, который предполагает самостоятельного решения. Ответы на все задачи приведены в конце пособия.
В текстах задач даются ссылки на Приложение, в котором содержатся глоссарий строительных терминов и их изображения.
Методические указания
Объемы геометрических тел
(1) объем параллелепипеда: V = a b
b  c, где a
c, где a b, c - линейные измерения параллелепипеда
b, c - линейные измерения параллелепипеда
(2) объем куба: V = a3, где а - сторона куба
(3) объем цилиндра: V = Sосн H = πR2H, где Sосн - площадь основания цилиндра, Н - высота цилиндра, R - радиус основания цилиндра
H = πR2H, где Sосн - площадь основания цилиндра, Н - высота цилиндра, R - радиус основания цилиндра
π = 3,14
(4) объем конуса: V = 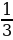 Sосн
Sосн H
H
(5) объем шара: V = 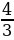 πR3, где R - радиус шара
πR3, где R - радиус шара
Площади поверхностей
(6) Площадь боковой поверхности параллелепипеда: Sбок= Pосн  H, где Pосн - периметр основания параллелепипеда,
H, где Pосн - периметр основания параллелепипеда,
Периметр плоской фигуры - сумма всех сторон фигуры
(7) Площадь полной поверхности параллелепипеда: Sпар-да =2Sосн + Sбок, где Sосн - площадь основания параллелепипеда
Так как в основании прямоугольного
параллелепипеда может лежать прямоугольник, то площадь основания Sосн = а  b, где а и b - стороны прямоугольника, а если квадрат, то Sосн = а2, где а - сторона квадрата.
b, где а и b - стороны прямоугольника, а если квадрат, то Sосн = а2, где а - сторона квадрата.
(8) Площадь боковой поверхности цилиндра: Sбок = 2πRH
(9) Площадь полной поверхности цилиндра: Sцил = 2πRH + 2πR2 = 2πR( H + R)
(10) Площадь боковой поверхности конуса: Sбок = πRL, где L - образующая конуса
(11) Площадь полной поверхности конуса: Sкон= πRL + πR2 = πR( L +R)
(12) Площадь сферы: Sсф= 4 πR2, где R - радиус сферы
Площади плоских фигур
(13) площадь прямоугольного треугольника: Sтр= 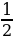 a b, где a и b - катеты треугольника
a b, где a и b - катеты треугольника
(14) площадь трапеции: Sтрап= 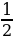 (a + b) h, где a и b - основания трапеции, h - высота трапеции, опущенной из одного основания на другое
(a + b) h, где a и b - основания трапеции, h - высота трапеции, опущенной из одного основания на другое
15) площадь прямоугольника: Sпрям = а  b, где а и b - стороны прямоугольника
b, где а и b - стороны прямоугольника
(16) площадь квадрата: Sкв = а2, где а - сторона квадрата.
(17) площадь круга: Sкр= πR2, где R - радиус круга
(18) длина окружности: С = 2πR, где R - радиус окружности
Некоторые величины и соотношения
В прямоугольном треугольнике:
(19) sinα = 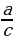 , где α - острый угол треугольника, а - противолежащий катет, с - гипотенуза
, где α - острый угол треугольника, а - противолежащий катет, с - гипотенуза
(20) cos α = 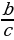 , где b - прилежащий катет
, где b - прилежащий катет
(21) tg α = 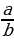
(22) 1% = 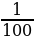 = 0,01
= 0,01
(23) m = V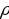 , где m - масса, V
, где m - масса, V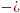 объем,
объем, 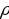 - плотность вещества
- плотность вещества
Пример1: Рассчитать необходимое количество бетона для заливки колонны (см.Приложение) со стороной основания 80см и высотой 4м.
Решение:
Чтобы рассчитать количество бетона, т.е. необходимый объем раствора, нужно воспользоваться для расчета формулой (1), т.к колонна имеет форму прямоугольного параллелепипеда.
Итак, V = a b
b  c, где a
c, где a 80 см ( 0,8м), b = 80 см (0,8м), c = 4 м.
80 см ( 0,8м), b = 80 см (0,8м), c = 4 м.
V = 0,8  0,8
0,8  4 = 2,56(м3)
4 = 2,56(м3)
Ответ: для заливки колонны необходимо бетонного раствора объемом 2,56 м3.
Пример2: Рассчитать расход бетонного раствора для заливки 10 канализационных колец с внутренним диаметром 1000 мм, внешним диаметром 1160 мм и высотой 900 мм. Сколько необходимо грузовых машин грузоподъемностью 5т для перевозки этих колец, если плотность бетона 2200 кг/ м3?
Решение:
Для того чтобы рассчитать расход бетонного раствора используем формулу для вычисления объема цилиндра (3) V = Sосн H = πR2H.
H = πR2H.
Объем кольца = объем внешнего цилиндра - объем внутреннего цилиндра.
1000мм= 1м, 1160мм=1,16м, 900мм= 0,9м
R и D - радиус и диаметр внешнего цилиндра, r и d - радиус и диаметр внутреннего цилиндра
R = 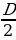 = 0,58м, r =
= 0,58м, r = 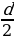 = 0,5м
= 0,5м
Объем внешнего цилиндра: V = 3,14  0,582
0,582  0,9 = 0,95 м3
0,9 = 0,95 м3
Объем внутреннего цилиндра: V = 3,14  0,52
0,52  0,9 = 0,7 м3
0,9 = 0,7 м3
Объем кольца = 0,95 - 0,7 = 0,25 м3
Для заливки одного кольца необходимо 0,25 м3 бетона.
для 10 колец = 0,25  10 = 2,5 м3 раствора.
10 = 2,5 м3 раствора.
Для расчета количества машин необходимо вычислить массу всех колец. Сначала вычислим массу одного кольца по формуле (23) m = V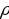 : m = 0,25
: m = 0,25 
2200 = 550 кг.
Масса 10 колец составляет = 550  10 = 5500кг = 5,5т.
10 = 5500кг = 5,5т.
рассчитаем количество машин = 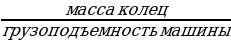 =
= 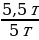 = 1,1 машины.
= 1,1 машины.
Ответ: для перевозки 10 канализационных колец необходимо 2 грузовые машины грузоподъемностью 5т.
Пример 3: Сколько потребуется банок краски ( 2,8кг) для окрашивания труб диаметром 60 мм длиной 100м, если на 1 м2 расходуется 200г краски?
Решение:
Сначала вычислим площадь поверхности труб, которые нужно окрасить. Для этого применим формулу для вычисления площади боковой поверхности цилиндра (8) Sбок = 2πRH.
60мм= 0,06м
R = 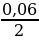 = 0,03м
= 0,03м
Sбок= 2  3,14
3,14  0,03
0,03  100 = 18,84м 2
100 = 18,84м 2
200г = 0,2кг
количество краски = Sбок  0,2 = 18,84
0,2 = 18,84  0,2 = 3,768 кг
0,2 = 3,768 кг
количество банок = 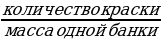 =
= 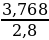
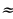 1,4 банки.
1,4 банки.
Ответ: Для окрашивания труб требуется 1,4 банки краски.
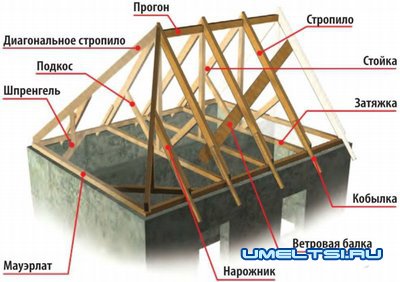
Пример 4: Какой должна быть стойка двускатной крыши при длине балки перекрытия 8м, чтобы угол наклона крыши был 300?
Решение:
Стойка, стропило и половина балки перекрытия составляют прямоугольный треугольник.
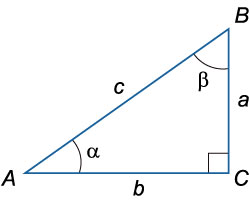
противолежащий катет b - стойка, прилежащий катет а - половина балки перекрытия, гипотенуза с - стропило,  A - угол наклона крыши.
A - угол наклона крыши.
Стойку крыши найдем по определению тангенса (21) tg α = 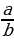
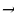
a = b  tg
tg  A = 4
A = 4  tg 300 = 4
tg 300 = 4 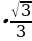 =
= 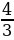
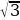 (м)
(м)
Ответ: Стойка двускатной крыши должна быть длиной 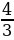
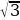 м при длине балки перекрытия 8 м, чтобы угол наклона крыши составлял 300.
м при длине балки перекрытия 8 м, чтобы угол наклона крыши составлял 300.
Задания для самостоятельной работы
1.1. Сколько необходимо заказать машин - бетонных миксеров объемом 5 м3 для того чтобы залить бетоном сплошной фундамент ( см.Приложение) размерами 8м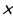 9м и высотой 70 см ?
9м и высотой 70 см ?
1.2. Рассчитать необходимое количество мешков цемента (вес мешка 50 кг), для того чтобы залить 3 плиты перекрытия размерами 5м, 2м и 30см, из расчета, что на 1 м3 раствора необходимо 100кг цемента.
1.3. Какое количества мешков песка нужно, для того чтобы замесить раствор для заливки 20 столбов столбчатого фундамента размерами 0,5 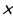 0,5
0,5 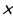 1 м, если в один мешок можно поместить 50 кг песка и на 1 м3 раствора идет 100кг песка?
1 м, если в один мешок можно поместить 50 кг песка и на 1 м3 раствора идет 100кг песка?
1.4. Сколько строительного кирпича и раствора потребуется для постройки стены длиной 12 м, толщиной 0,5 м и высотой 2,5 м, если в 1 м3 кирпичной кладки содержится 400 шт. кирпича, а потребность в растворе составляет 0,2 объема кладки.
2.1.Рассчитать расход бетонного раствора для заливки ленточного фундамента высотой 0,8 м, внешними размерами 8,5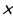 7,5м и внутренними размерами 8
7,5м и внутренними размерами 8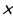 7м. Каким объемом нужен бетонный миксер для доставки раствора потребителю?
7м. Каким объемом нужен бетонный миксер для доставки раствора потребителю?
2.2. Сколько потребуется бетона для того чтобы залить швеллер с параллельными гранями полок 12П длиной 10м?
2.3. Сколько понадобится кирпичей ( 250  65
65  120мм), чтобы выстроить коробку размерами 9м, 12 м и высотой 3м и толщиной стен в 48см?
120мм), чтобы выстроить коробку размерами 9м, 12 м и высотой 3м и толщиной стен в 48см?
2.4. Рассчитать необходимое количество бетона, необходимое для того чтобы изготовить четырехугольный колодец кабельной связи, если размеры колодца 1400мм 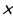 1400мм
1400мм 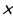 835мм, радиус люка 350 мм, сторона ниши 290мм при толщине стенок колодца 70 мм.
835мм, радиус люка 350 мм, сторона ниши 290мм при толщине стенок колодца 70 мм.
3.1. Сколько потребуется приобрести рулонов материала для изоляции труб длиной 50 м диаметром 460 мм, если длина материала в рулоне 10 м, а ширина 1,5 м?
3.2. Рассчитайте сколько потребуется мешков (30кг) сухой строительной смеси (расход 8,5кг/м2 при толщине слоя 10мм) для отделки поверхности длиной 5м и шириной 2,5м при толщине слоя 23мм?
3.3. Какой длины утеплитель шириной 3м потребуется для утепления стен помещения 3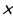 3
3 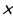 5м ?
5м ?
3.4. Нужно оклеить обоями комнату, длина которой 6 м, ширина 4 м, высота 3 м, площадь дверей и окон составляет 1/5 всей площади стен. Сколько потребуется рулонов обоев для оклейки, если длина рулона 12 м, а ширина 50 см?
4.1. Какой длины надо изготовить стропила для дома 6м 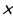 7м, если стойка крыши составляет1,5 м?
7м, если стойка крыши составляет1,5 м?
4.2. Рассчитать количество листов шифера (980мм 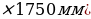 , необходимого для дома 9м
, необходимого для дома 9м 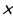 12м, если стойка крыши 1,5м.
12м, если стойка крыши 1,5м.
4.3. Во сколько обойдется покупка металлочерепицы (245руб/м2) на крышу (уклон крыши составляет 300) деревянного дома размерами 6м 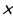 6м при этом запас составляет 15% от всей площади крыши?
6м при этом запас составляет 15% от всей площади крыши?
4.4. Какова должна быть длина стойки крыши, чтобы стропила были длиной 5м , а балка перекрытия 8м? Рассчитать количество досок шириной 200мм и длиной 4м для того чтобы закрыть фронтон.
Ответы к задачам
1.1. 11 машин
1.2. 18 мешков
1.3. 100 мешков
1.4. 6000 штук и 3 м3 раствора
2.1. 6,2 м3 ; 7м3
2.2.0,0543 м3
2.3. 29744 штук
2.4. 0,27 м3
3.1. 5 рулонов
3.2. 8 м
3.3. 16 м
3.4. 8 рулонов
4.1. 3,3 м
4.2. 66 листов
4.3.11495,4 руб
4.4. 15 досок
Приложение
Виды фундаментов



сплошной столбчатый ленточный
Колодцы

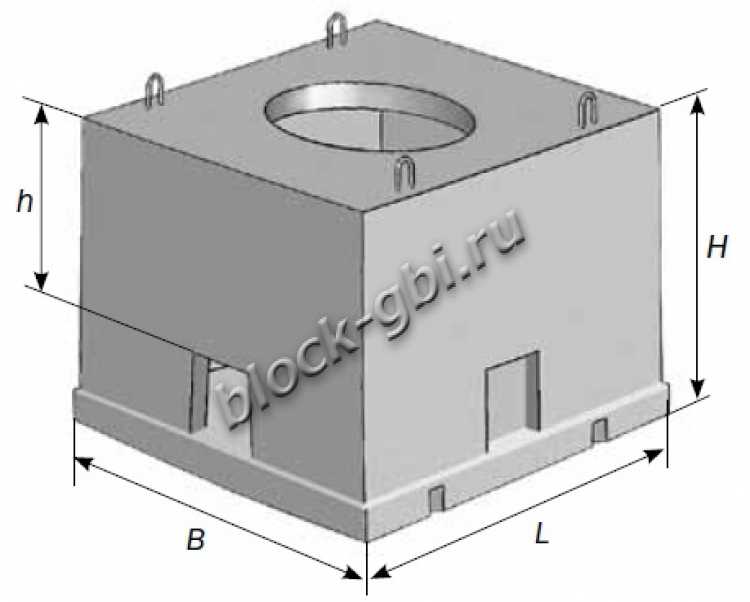
канализационный колодец кабельной связи

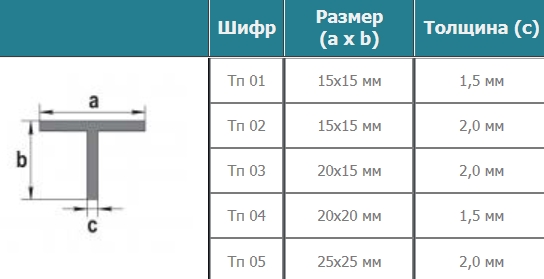
тавр


двутавр швеллер
Двускатная крыша Колонна

Плиты перекрытия

Глоссарий
Двутавр или двутавровая балка - мощный элемент армирования сварной конструкции, который выглядит как соединенные между собой две буквы «Т». Именно отсюда и пошло название «двутавра».
Крыша - верхняя часть строения, покрывающая его и служащая защитой от атмосферных явлений.
Тавр - (тавровая балка - тавровый профиль), Профиль металлический.
Фундамент сооружения – подземная часть сооружения, служащая для передачи и распределения давления от сооружения на грунт:
Швеллер – это гнутый металлический профиль, с П-образным сечением, основное назначение которого – служить несущим элементом при возведении строительных конструкций.








 b
b  b, c - линейные измерения параллелепипеда
b, c - линейные измерения параллелепипеда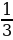 Sосн
Sосн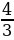 πR3, где R - радиус шара
πR3, где R - радиус шара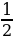 a b, где a и b - катеты треугольника
a b, где a и b - катеты треугольника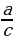 , где α - острый угол треугольника, а - противолежащий катет, с - гипотенуза
, где α - острый угол треугольника, а - противолежащий катет, с - гипотенуза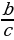 , где b - прилежащий катет
, где b - прилежащий катет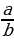
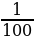 = 0,01
= 0,01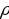 , где m - масса, V
, где m - масса, V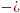 объем,
объем,  80 см ( 0,8м), b = 80 см (0,8м), c = 4 м.
80 см ( 0,8м), b = 80 см (0,8м), c = 4 м.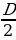 = 0,58м, r =
= 0,58м, r = 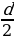 = 0,5м
= 0,5м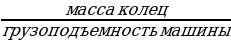 =
= 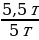 = 1,1 машины.
= 1,1 машины.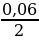 = 0,03м
= 0,03м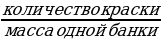 =
= 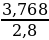
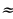 1,4 банки.
1,4 банки.
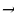
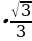 =
= 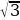 (м)
(м)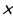 9м и высотой 70 см ?
9м и высотой 70 см ?
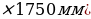 , необходимого для дома 9м
, необходимого для дома 9м 





















