Algebraik droblary köpeltmek, bölmek we derejä götermek
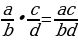 (1)
(1)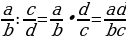 (2)
(2) 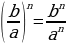 (3)
(3)
Arifmetik kwadrat kök.
 =b, bu ýerde b ≥ 0 we
=b, bu ýerde b ≥ 0 we  =a
=a 
 a bu ýerde a ≥ 0
a bu ýerde a ≥ 0
Arifmetik kwadrat köküň häsiýetleri
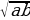 =
= •
• 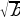 (1)
(1)  =
=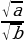 (2)
(2)  |x| (3)
|x| (3)
Kwadrat deňlemäniň kökleriniň formulasy
a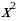 +bx+c =0 (1)
+bx+c =0 (1) 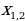 =
=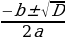 , bu ýerde D=
, bu ýerde D=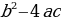
Bitin görkezijili derejäniň häsiýetleri
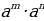 =
=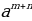 (1)
(1) 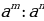 =
=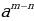 (2)
(2)  =
= (3)
(3) =
=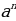 ·
·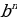 (4)
(4) 
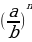 =
= 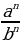 (5)
(5)  =1 (6)
=1 (6)  =
= (7)
(7)
Rasional görkezijili dereje we onuň häsiýetleri
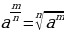 a0, n ≥ 2
a0, n ≥ 2 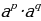 =
= (1)
(1)
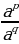 =
=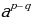 (2)
(2) 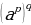 =
= (3)
(3)
 =
=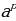 ·
·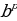 (4)
(4)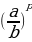 =
= 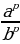 (5)
(5)
Eger o 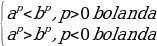 (6)
(6)
Eger p 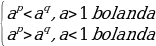 (7)
(7)
n-nji derejeli arifmetik köküň häsiýetleri
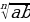 =
=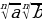 (1)
(1)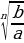 =
= 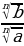 (2)
(2)
 =
=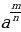 (3) (
(3) ( )m =
)m = (4)
(4)
 =
= (5)
(5)  =
=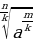 (6)
(6)
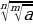 =
= (7) 0≤a
(7) 0≤a

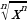 =
=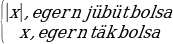
 köküň bahasy
köküň bahasy 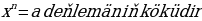
GYSGA KÖPELTMEK FORMULALARY
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2
(a+b)3 = a3+3a2b+ 3ab2 + b3
(a - b)3 = a3- 3a2b+ 3ab2 - b3
a3+b3 = (a+b)·(a2- ab+b2)
a3- b3 = (a - b)·(a2+ ab+b2)
a2- b2 = (a-b)·(a+b)
Köpgranlyklaryň göwrümleri
Gönüburçly parallelepipediň göwrümi V=a·b·c
Kubuň göwrümi V=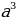
Göni prizmanyň göwrümi V=S·H
Ýapgyt prizmanyň göwrümi V=S·L ýa-da V=Q·H
Bu ýerde S- perpendikulýar kesik, Q-esasynyň meýdany, L-gapdal gapyrgasy,H-beýiklik
Piramidanyň göwrümi V=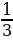 QH
QH
Kesilen piramidanyň göwrümi V= 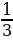 H(Q+
H(Q+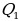 +
+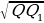 )
)
Meňzeş jisimleriň göwrümleriniň gatnaşygy
 =
= 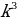
ÖNÜM , С
, С =0, x'=1,
=0, x'=1,  )'=2x
)'=2x
(kx +b)'= k,  (
( )'=
)'= 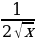 , (
, (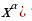 =α
=α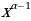
Önümi hasaplamagyň düzgünleri
(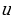 +
+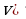 =
= 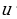 +
+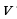 (1) (
(1) (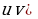 =
= 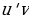 +
+ (2)
(2)
(C 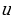 )
) = C
= C 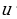 (3)
(3) 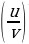 =
= 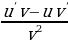 (4)
(4)
f(x)=φ(g(x)) bolsa,onda 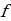 (x)=φ
(x)=φ (g(x))· g
(g(x))· g (x)
(x)
Trigonometrik funksiýalaryň önümleri
(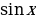 )
) = cos
= cos (1) (
(1) (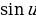 )
) =
=  cos
cos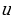 (2)
(2)
(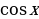 )
) = -
= -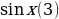 (
(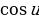 )
) = -
= -
(tg )
) =
= (5) (tgu)
(5) (tgu) =
= (6)
(6)
(ctg )
) =
=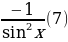 (ctg
(ctg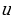 )
) =
= (8)
(8)
Esasy trigonometrik toždestwolar.
 tg
tg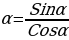 Ctg
Ctg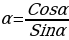
tgα·Ctgα = 1 1+tg2α =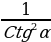 1+ctg 2α =
1+ctg 2α =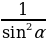
Goşmak formulalary
Sin(α+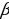 )=SinαCos
)=SinαCos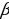 +CosαSin
+CosαSin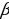 Sin(α-
Sin(α-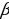 )=SinαCos
)=SinαCos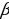 -CosαSin
-CosαSin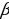 Cos(α+
Cos(α+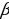 )=GosαCos
)=GosαCos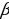 -SinαSin
-SinαSin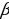 Cos(α-
Cos(α-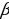 )=GosαCos
)=GosαCos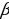 +SinαSin
+SinαSin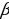
tg(α+β)=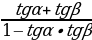 tg(α-β)=
tg(α-β)=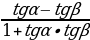
Ctg(α+β)=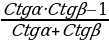 Ctg(α-β)=
Ctg(α-β)=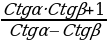
Ikeldilen burçuň trigonometrik funksiýalary
Sin2α=2Sinα·Cosα Cos2α=Cos2α –Sin2α
Cos2α=1-2Sin2α Cos2α=2Cos2α –1
tg2α=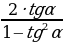 Ctg2α=
Ctg2α= 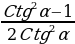
Üçeldilen burçuň trigonometrik funksiýalary
Sin3α=3Sinα- 4 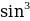 α Cos3α=4Cos3α –3Сosα
α Cos3α=4Cos3α –3Сosα
tg3α=
Ýarym burçuň trigonometrik funksiýalary
Sin
 Cos
Cos
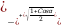
tg
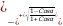 Ctg
Ctg
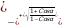
Ýarym burçuň tangensi arkaly aňlatmak
Sinα=  Cosα=
Cosα= 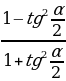 tgα=
tgα=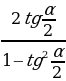
Ctgα=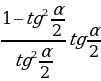 =
=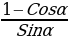 =
= 
Derejäni peseltmegiň formulalary
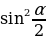 =
= 
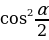 =
= 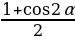
Jemi köpeltmek hasylyna öwürmegiň formulasy.
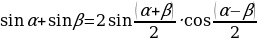
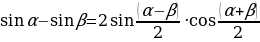
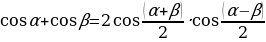
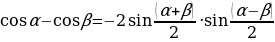
tgα+tgβ=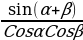 tgα-tgβ=
tgα-tgβ=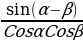
Ctgα+Ctgβ= Ctgα-Ctgβ=
Ctgα-Ctgβ=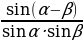
Köpeltmek hasylyny jeme öwürmegiň formulasy.
SinαSinβ=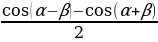 SinαCosβ=
SinαCosβ= 
CosαCosβ = 
Kwadrat üçagzany köpeldijilere dagytmak
ax2 + bx + c = a(x-x1)(x-x2)
Kwadrat üçagzadan ikiagzanyň kwadratyny bölüp çykarmak
ax2 + bx + c = a(x-m)2 + n
Funksiýanyň grafiginiň ýönekeý özgertmeleri
y= f (x-m)+ n
Ýönekeý diofant deňlemeleriniň çözülişi
(x0;y0) ax2 + bx + c =0 deňlemäniň haýsydyr bir çözüwi bolsa , onda onuň galan ähli çösüwleri
x = x0-bt, y = y0+ at
formula bilen tapylýar
Wektorlary skalýar köpeltmek
 (1),
(1), 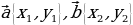 (2)
(2)



(3)






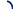


α
0
Cosα=
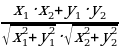
(4)
Dogry köpburçluklar
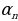 =
=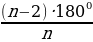 , n=
, n= 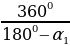 ,
, 
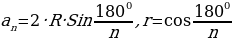

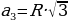 ,
,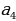 =R·
=R· ,
, = R
= R


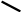




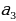
R
r

O
Dogry köpburçlugyň meýdany
S= 
Arifmetik progressiýa
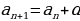
 =
=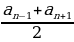
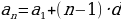
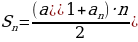
Geometrik rpogressiýa
 ,
,  = ԛ,
= ԛ,  =
=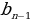 ·
·
 =
=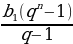 ,
,  =
= , ԛ≠1
, ԛ≠1
S=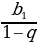
Ýönekeý we çylşyrymly göterimler
 )
) 
Şol bir argumentli trigonometrik funksiýalaryň arasyndaky gatnaşyk
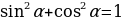
tgα = , Ctgα =
, Ctgα = 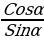
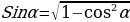

Hakyky görkezijili derejäniň häsiýetleri
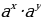 =
=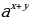 (1)
(1) 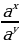 =
= (2)
(2) 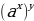 =
=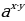 (3)
(3)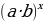 =
=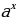 ·
·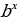 (4)
(4) 
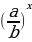 =
= 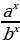 (5)
(5) 
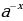 =
=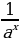 (6)
(6)
Logarifmler
 ,
, 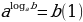 ,
, 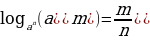 (2)
(2)
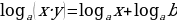 (3)
(3)
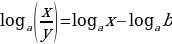 (4)
(4)
 =k
=k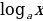 (5)
(5)
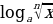 =
=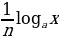 (6)
(6) =
=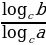 (7)
(7)
 =-
=-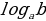 (8)
(8)

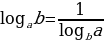 (10)
(10)
Predeller

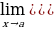
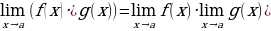


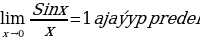


Funksiýanyň artdyrmasy
△x=x-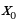 ýa-da x=
ýa-da x=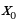 +△x
+△x
△f=f(x)-f(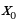 )=f(
)=f(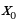 +△x)- f(
+△x)- f(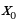 )
)
f(x)=f(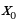 +△x)= f(
+△x)= f(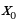 )+△f
)+△f
Trigonometrik deňlemeleriň çözülişi
1) Sinx=a -1k·arcsina+k
Sinx=1 x=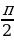 +2k
+2k
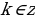
Sinx=0 x= 
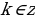
Sinx=-1 x=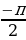 +2k
+2k
2) Cos x=a -1 x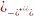 arccosa+2k
arccosa+2k
Cos x=1 x= 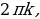
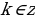
Cos x=0 x=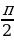 +2k
+2k
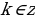
Cos x=-1 x=  +2k
+2k
3. tg(x)=a x= arctga+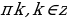
tg(x)=0 x= 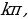
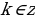
4. Ctg(x)=a x= arctga+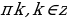
Ctg(x)=0 x=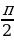 +k
+k
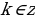
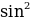 x=a 0
x=a 0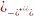 arcsin
arcsin +k
+k
 x=a 0 x
x=a 0 x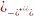 arccos
arccos +k
+k
tg2(x)=a 0∞ x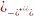 arctg
arctg +
+
Ctg2(x)=a 0∞ x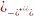 arcctg
arcctg +
+
Sinα=Sinβ α-β=2k ýa-da α+β=(2k+1)
ýa-da α+β=(2k+1)
Cosα = Cosβ α+β= ýa-da α-β=2k
ýa-da α-β=2k
tgα= tgβ α- β=k we α≠(2k+1)
we α≠(2k+1)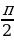 ,β≠(2k+1)
,β≠(2k+1)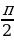
Ctgα =Gtgβ α-β=k  we α≠k
we α≠k , β≠ k
, β≠ k
Paskalyň üçburçlugy
| 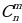
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 2n |
| 0 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
| 1 | 1 | 1 |
|
|
|
|
|
|
|
|
|
|
|
| 2 |
| 2 |  1 1
| 2 | 1 |
|
|
|
|
|
|
|
|
|
|
| 4 |
| 3 | 1 | 3 | 3 | 1 |
|
|
|
|
|
|
|
|
|
| 8 |
| 4 | 1 | 4 |  6 6
| 4 | 1 |
|
|
|
|
|
|
|
|
| 16 |
| 5 | 1 | 5 | 10 | 10 | 5 | 1 |
|
|
|
|
|
|
|
| 32 |
| 6 | 1 | 6 | 15 |  20 20
| 15 | 6 | 1 |
|
|
|
|
|
|
| 64 |
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
|
|
|
|
|
| 128 |
| 8 | 1 | 8 | 28 | 56 |  70 70
| 56 | 28 | 8 | 1 |
|
|
|
|
| 256 |
| 9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
|
|
|
| 512 |
| 10 | 1 | 10 | 45 | 120 | 210 |  252 252
| 210 | 120 | 45 | 10 | 1 |
|
|
| 1024 |
| 11 | 1 | 11 | 55 | 165 | 330 | 462 |  462 462
| 330 | 165 | 55 | 11 | 1 |
|
| 2048 |
| 12 | 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 |
| 4096 |
| 13 | 1 | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 | 78 | 13 | 1 | 4192 |


B
Göniburçly üçburçlugyň ýiti burçunyň sinusy, kosinusy, tangensi. 
gipotenuza


katet
katet


C
A
1.A burçuň garşysynda ýatan katetiň gipotenuza bolan gatnaşygyna A burçuň sinusy diýilýär
SinA= 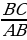
2.A burça sepleşýän katetiň gipotenuza bolan gatnaşygyna A burçuň kosinusy diýilýär
CosA=
3.A burçuň garşysynda ýatan katetiň sepleşýän katete bolan gatnaşygyna A burçuň tangensi diýilýär
tg A= 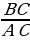
Käbir burçlar üçin trigonometrik funksiýalaryň bahalary
| 
|  I I
|   II II
|   III III
|   IV IV
|
| 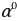
| 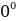
| 
| 
| 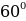
| 
| 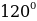
| 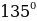
| 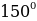
| 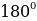
| 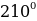
| 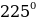
| 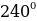
| 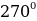
| 
| 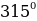
| 
| 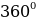
|
| 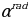
| 0 | 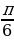
| 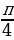
| 
| 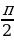
| 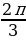
| 
| 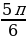
| 
| 
| 
| 
| 
| 
| 
| 
| 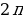
|
| Sinα | 0 | 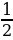
| 
| 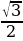
| 1 | 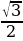
| 
| 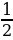
| 0 | 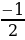
| 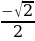
| 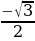
| -1 | -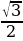 | - | -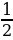 | 0 |
| Сosα | 1 | 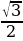
| 
| 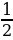
| 0 | -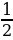 | 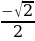
| 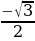
| -1 | 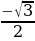
| - | 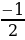
| 0 | 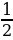
| 
| 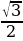
| 1 |
| tgα | 0 | 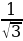
| 1 | 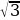
| ∞ | 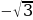
| -1 | -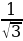 | 0 | 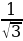
| 1 | 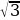
| ∞ | 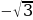
| -1 | -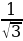 | 0 |
| ctgα | ∞ | 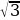
| 1 | 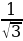
| 0 | 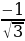
| -1 | 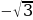
| ∞ | 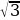
| 1 | 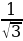
| 0 | 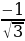
| -1 | 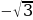
| ∞ |
Käbir burçlar üçin trogonometrik funksiýalaryň bahalary
| 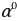
| 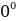
| 
| 
| 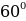
| 
|
|
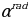
|
0 | 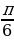
| 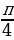
| 
| 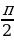
|
| Sinα |
0 | 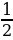
| 
| 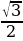
|
1 |
| Сosα |
1 | 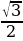
| 
| 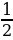
|
0 |
| tgα |
0 | 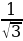
|
1 |
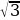
|
∞ |
| ctgα |
∞ |
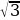
|
1 | 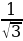
|
0 |
Asyl funksiýalary tapmagyň käbir formulalary
| f(x) | k | Xα | 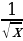
| Sinx | Cosx | 
| 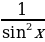
| 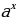
| 
| 
| 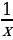
|
| F(X)+С | kx+c | 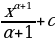
|
2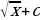 |
-Cosx+c |
Sinx+c | tgx+c |
-Ctgx+c | 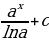
|

| 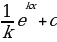
|

|
Asyl funksiýany tapmagyň üç düzgüni
f üçin F, g üçin G asyl funksiýa bolsa, onda
f + g üçin F+G asyl funksiýadyr.
f üçin F asyl funksiýa bolsa ,onda k·f üçin k·F asyl funksiýadyr.
f(x) üçin F(X) asyl funksiýa bolsa, onda f(kx +b)
üçin  F(kx+b) asyl funksiýadyr.
F(kx+b) asyl funksiýadyr.
Sferanyň deňlemesi.
1.Merkezi O(0;0;0)nokatda bolan sferanyň deňlemesi x2+y2+z2=R2 (1)
2. Merkezi C0(x0;y0;z0)nokatda bolan sferanyň deňlemesi
(x-x0)2+(y-y0)2+(z-z0)2=R2 (2)
Tekizligiň deňlemesi
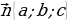 wektora perpendikulýar bolan tekizligiň deňlemesi
wektora perpendikulýar bolan tekizligiň deňlemesi
ax+by+cz+d = 0 (3)
Nokatdan tekizlige çenli uzaklygy tapmagyň formulasy
M(x;y;z) nokatdan 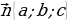 wektora perpendikulýar bolan ax+by+cz+d = 0 deňleme bilen berilen tekizlige çenli uzaklyk
wektora perpendikulýar bolan ax+by+cz+d = 0 deňleme bilen berilen tekizlige çenli uzaklyk
l = (4)
(4)
Wektorlary skalýar köpeltmek
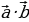 =|
=| |·|
|·| |·Cosα =x·x1+y·y1+z·z1 (5)
|·Cosα =x·x1+y·y1+z·z1 (5)
Nokadyň we wektoryň koordinatalarynyň arabaglanyşygy
A(x1,y1,z1) we B(x2,y2,z2) bolsa ,onda
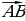 {x2-x1;y2-y1;z2-z1} (1)
{x2-x1;y2-y1;z2-z1} (1)
| |=
|=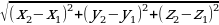 (2)
(2)
Giňişlikde iki nokadyň arasyndaky uzaklyk
Eger M(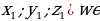 M(
M( bolsa ,onda
bolsa ,onda
d=| |=
|=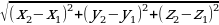 (3)
(3)
Giňişlikde iki göni çyzygyň arasyndaky burçuň kosinusy
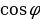 =
= 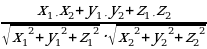 (4)
(4)
Göni çyzyk bilen tekizligiň arasyndaky burçuň sinusy.
Eger P{ x1,y1,z1} göni çyzygyň ugrukdyryjy wektory, 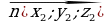 } α tekizlige perpendikulýar wektor bolsa , onda
} α tekizlige perpendikulýar wektor bolsa , onda
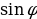 =
= 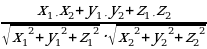 (5)
(5)


a
a
Kwadratyň ,gönüburçlugyň,parallelogramyň , üçburçlugyň,trapesiýanyň meýdany. 








b
b
a






a
a

a
S=a
2 S= a·b







h
h
b
b




a
a
S= a ·h S= 0,5·a ·h
Pifagoryň teoremasy

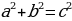


b
c
a
2 = c
2 – b
2 
a
b
2 =c
2 – a
2 Güberçek n – burçlugyň burçlarynyň jemi
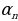 =
=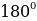 ·(n-2)
·(n-2)



B
Ç
B
Üçburçlugyň we trapesiýanyň orta çyzygy 











D
A
E
F
E
F
Ç
A
EF||AC EF||BC, EF||AD
EF=0,5AC EF=0,5(AD+BC)
Gönüburçly üçburçlukda proporsional kesimler
h =  a =
a = 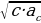
b = 





h
a

b




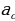

c
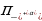 , 2
, 2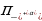 we ş.m burçlar üçin getirme formulalary
we ş.m burçlar üçin getirme formulalary
 | π+α | π-α | 2π+α | 2π-α | 3π+α | 3π-α | 4π+α | 4π-α |
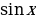 |  | 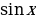 | 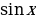 |  |  | 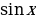 | 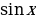 |  |
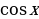 | 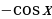 | 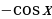 | 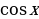 | 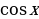 | 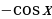 | 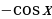 | 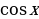 | 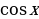 |
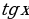 | 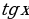 |  | 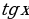 |  | 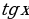 |  | 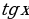 |  |
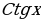 |  | 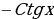 | 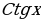 | 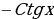 | 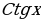 | 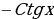 | 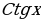 | 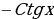 |
 ,
, 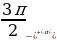 we ş.m burçlar üçin getirme formulalary
we ş.m burçlar üçin getirme formulalary
Görkezijili funksiýanyň önümi.
( )̍ =
)̍ =  (1) (
(1) ( )′ =u′·
)′ =u′· (2)
(2)
(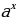 )̍ =
)̍ = 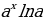 (3) (
(3) ( )′ =u′·
)′ =u′· ln a (4)
ln a (4)
Logarifmik funksiýanyň önümi
(lnx)′=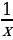 (1) (lnu)′=
(1) (lnu)′= (2)
(2)
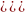 =
=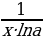 (3)
(3)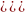 =
=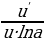 (4)
(4)
Ters funksiýanyň önümi
F we g özara ters funksiýalar we f funksiýanyň 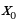 nokatda önümi bolup , ol hem nola deň däl bolsun, onda
nokatda önümi bolup , ol hem nola deň däl bolsun, onda 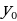
 =f(
=f(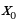 )) nokatda g funksiýanyň önümi bardyr.
)) nokatda g funksiýanyň önümi bardyr.
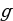 (
(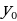 ) =
) = 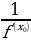
Galtaşýan çyzygyň deňlemesi we ýakynlaşan hasaplamalar.
 y=
y= 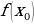 +
+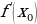 ·(x-
·(x- 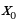 )
)
f(x)= 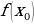 +
+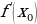 ·△x (1+△x)n ≈1+n·△x
·△x (1+△x)n ≈1+n·△x
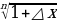 ≈1+
≈1+
Sin (x0+△x) ≈ Sin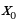 +△xCos x0 (x0+△x)n ≈
+△xCos x0 (x0+△x)n ≈ +n
+n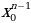 ·△x
·△x
 ≈
≈ 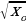 +
+
 ≈1+
≈1+


B1
B
Üçburçluklaryň meňzeşlik nyşanlary 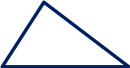





C
A
A1
C1

s
I.Eger 1, 1 onda △ABC △A1 B 1C1 
s
II. Eger 1,  onda △ABC △A1 B 1C1
onda △ABC △A1 B 1C1 
s
III.Eger 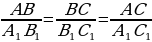 , onda △ABC △A1 B 1C1ч
, onda △ABC △A1 B 1C1ч 

B1
B
Üçburçluklaryň meýdanlarynyň gatnaşygy 





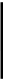






h
h1
a
b
A
A1
C
C1
1
Eger 1, onda 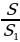 =
= 
Eger h = h1 bolsa , onda 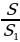 =
= 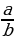

s
Eger △ABC △A1 B 1C1,onda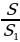 = k2
= k2


B
Üçburçlugyň bissektrisasynyň häsiýeti 
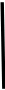


1
2



D
C
A
Eger bolsa, onda 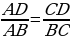
Iki hordanyň, iki kesijiniň we galtaşýan çyzyk bilen hordanyň arasyndaky burç



B
B



























D
E
B
O
O
O
·
·
·
D
C
E
C
C
D
A
A
A



3
1
2


2)
1)
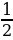 (ᴗAC+ᴗDE)
(ᴗAC+ᴗDE) 
3)

С
Köpburçlugyň ortogonal proýeksiýasynyň meýdany. 


 So.pr=S·cosφ
So.pr=S·cosφ







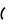

φ
С2
B
С1


A
α
Iki wektoryň kollinearlyk nyşany
 =k·
=k· (1) deňlik ýerine ýetmeli .Bu ýerde
(1) deňlik ýerine ýetmeli .Bu ýerde
 we
we  nol däl wektorlar.
nol däl wektorlar.
Üç wektoryň komplanarlyk nyşany.
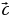 = х
= х  +y
+y (2) deňlik ýerine ýetmeli
(2) deňlik ýerine ýetmeli
Wektory komplanar däl üç wektor boýunça dagytmak
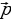 = х
= х  +y
+y + z
+ z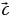 (3)
(3)
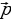 = х
= х  +y
+y + z
+ z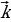 (4)
(4) 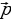 { х ,y,z}
{ х ,y,z}
Kwadrat üçagza we onuň kökleri
ax2 + bx + c görnüşli köpagza kwadrat üçagza diýilýär
x üýtgeýän ululygyň kwadrat üçagzanyň bahasyny nola deňleýän bahalaryna kwadrat üçagzanyň kökleri diýilýär.
Kwadrat üçagzanyň köklerini tapmak üçin ax2 + bx + c = 0 kwadrat deňlemäni çözmek ýeterlikdir.
Mysal. 2x2 - 3x + 1 kwadrat üçagzanyň köklerini tapalyň. Kwadrat üçagzanyň köklerini tapmak üçin 2x2 - 3x + 1 = 0
deňlemäni çözmeli
D=(-3)2- 4·2·1=9-8=1
X1,2= 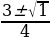 ; X1=1, X2 =
; X1=1, X2 = 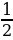 . Diýmek
. Diýmek
2x2 - 3x + 1 kwadrat üçagzanyň 1-e we 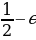 deň bolan iki sany köki bar.
deň bolan iki sany köki bar.
Kwadrat üçagzany köpeldijilere dagytmak
Teorema.Eger x1 we x2 sanlar
ax2 + bx + c kwadrat üçagzanyň kökleri bolsa,onda
ax2 + bx + c = a(x-x1)(x-x2)
deňlik dogrudyr.
Kwadrat üçagzanyň diskriminanty nola deň bolan ýagdaýynda onuň iki sany deň köki bardyr.
Kwadrat üçagzadan ikiagzanyň kwadratyny bölüp çykarmak
ax2 + bx + c = a(x-m)2 + n
Funksiýanyň grafiginiň ýönekeý özgertmeleri
y= f (x-m)+ n
Natural görkezijili derejäniň häsiýetleri
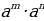 =
=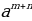 (1)
(1) 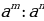 =
=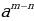 (2)
(2)  =
= (3)
(3)  =
=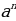 ·
·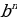 (4)
(4) 
 =1 (5)
=1 (5) 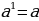 (6)
(6)
Köpagzalary goşmak we aýyrmak
Köpagzalary goşmak ýa-da aýyrmak ücin, olary jem ýa-da tapawut görnüşinde ýazmaly, soňra ýaýlary açmaly we meňzeş goşulyjylary toplamaly
(x+6y)+(3-4y)=x+6y+3-4y=6y-4y+x+3=2y+x+3






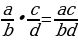 (1)
(1)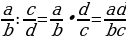 (2)
(2) 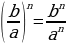 (3)
(3) =b, bu ýerde b ≥ 0 we
=b, bu ýerde b ≥ 0 we  =a
=a 
 a bu ýerde a ≥ 0
a bu ýerde a ≥ 0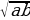 =
=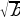 (1)
(1)  =
=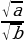 (2)
(2)  |x| (3)
|x| (3) 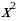 +bx+c =0 (1)
+bx+c =0 (1) 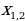 =
=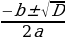 , bu ýerde D=
, bu ýerde D=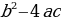
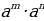 =
=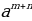 (1)
(1) 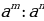 =
=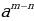 (2)
(2)  =
= (3)
(3) =
=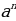 ·
·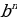 (4)
(4) 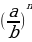 =
= 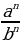 (5)
(5)  =1 (6)
=1 (6)  =
= (7)
(7)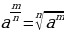 a0, n ≥ 2
a0, n ≥ 2 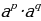 =
= (1)
(1)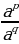 =
=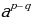 (2)
(2) 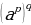 =
= (3)
(3) =
=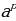 ·
·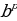 (4)
(4)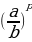 =
= 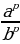 (5)
(5)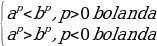 (6)
(6)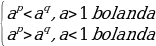 (7)
(7)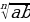 =
=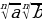 (1)
(1)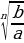 =
= 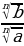 (2)
(2) =
=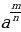 (3) (
(3) ( )m =
)m = (5)
(5) 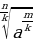 (6)
(6)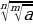 =
= (7) 0≤a
(7) 0≤a
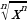 =
=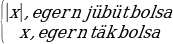
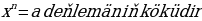
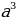
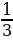 QH
QH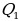 +
+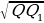 )
) =
= 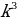
 , С
, С =0, x'=1,
=0, x'=1,  )'=2x
)'=2x  (
( )'=
)'= 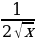 , (
, (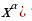 =α
=α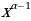
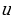 +
+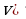 =
= 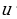 +
+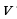 (1) (
(1) (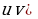 =
= 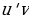 +
+ (2)
(2) 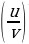 =
= 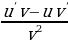 (4)
(4)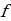 (x)=φ
(x)=φ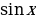 )
) (1) (
(1) (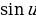 )
) cos
cos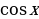 )
)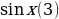 (
(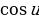 )
)
 (5) (tgu)
(5) (tgu) (6)
(6) 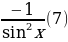 (ctg
(ctg (8)
(8) tg
tg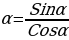 Ctg
Ctg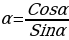
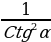 1+ctg 2α =
1+ctg 2α =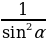
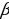 )=SinαCos
)=SinαCos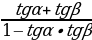 tg(α-β)=
tg(α-β)=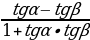
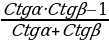 Ctg(α-β)=
Ctg(α-β)=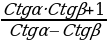
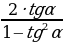 Ctg2α=
Ctg2α= 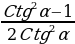
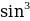 α Cos3α=4Cos3α –3Сosα
α Cos3α=4Cos3α –3Сosα

 Cos
Cos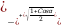
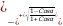 Ctg
Ctg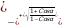
 Cosα=
Cosα= 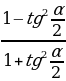 tgα=
tgα=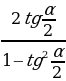
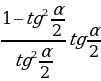 =
=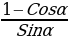 =
= 
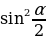 =
= 
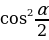 =
= 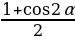
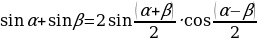
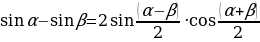
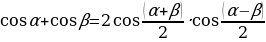
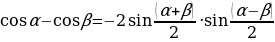
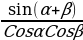 tgα-tgβ=
tgα-tgβ=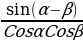
 Ctgα-Ctgβ=
Ctgα-Ctgβ=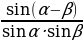
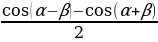 SinαCosβ=
SinαCosβ= 

 (1),
(1), 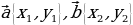 (2)
(2)

 (3)
(3) 





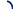


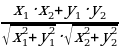 (4)
(4) 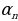 =
=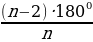 , n=
, n= 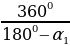 ,
, 
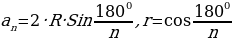

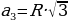 ,
, =R·
=R· ,
, = R
= R

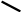




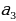

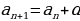
 =
=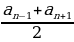
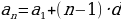
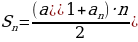
 ,
,  = ԛ,
= ԛ,  =
=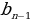 ·
·
 =
=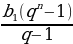 ,
,  , ԛ≠1
, ԛ≠1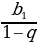
 )
) 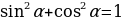
 , Ctgα =
, Ctgα = 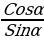
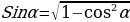

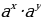 =
=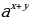 (1)
(1) 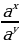 =
= (2)
(2) 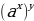 =
=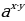 (3)
(3)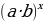 =
=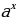 ·
·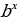 (4)
(4) 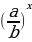 =
= 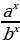 (5)
(5) 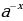 =
=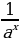 (6)
(6) ,
, 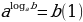 ,
, 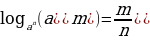 (2)
(2)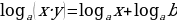 (3)
(3)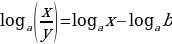 (4)
(4) =k
=k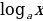 (5)
(5)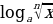 =
=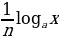 (6)
(6)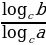 (7)
(7) =-
=-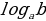 (8)
(8)
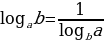 (10)
(10)
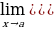
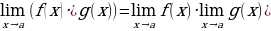


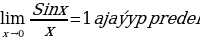

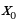 ýa-da x=
ýa-da x=
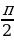 +2k
+2k
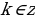

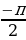 +2k
+2k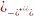 arccosa+2k
arccosa+2k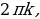
 +2k
+2k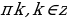
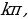
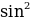 x=a 0
x=a 0 x=a 0 x
x=a 0 x
 ýa-da α-β=2k
ýa-da α-β=2k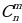
 1
1 252
252 462
462



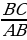

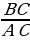

 I
I
 II
II
 III
III
 IV
IV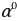
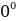


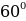

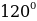
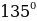
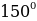
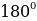
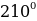
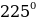
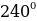
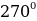

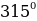

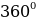
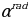
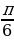
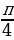

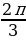

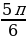







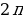
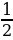

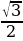
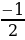
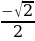
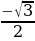
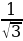
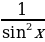


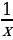
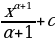
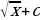
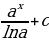

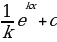

 F(kx+b) asyl funksiýadyr.
F(kx+b) asyl funksiýadyr.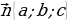 wektora perpendikulýar bolan tekizligiň deňlemesi
wektora perpendikulýar bolan tekizligiň deňlemesi (4)
(4)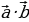 =|
=| {x2-x1;y2-y1;z2-z1} (1)
{x2-x1;y2-y1;z2-z1} (1)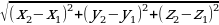 (2)
(2)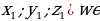 M(
M( bolsa ,onda
bolsa ,onda  |=
|=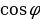 =
= 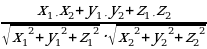 (4)
(4)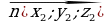 } α tekizlige perpendikulýar wektor bolsa , onda
} α tekizlige perpendikulýar wektor bolsa , onda 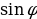 =
= 









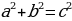






 a =
a = 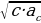










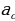

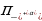 , 2
, 2
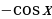
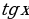

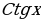

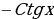
 ,
, 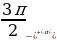 we ş.m burçlar üçin getirme formulalary
we ş.m burçlar üçin getirme formulalary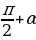
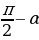


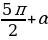



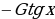
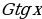
 )′ =u′·
)′ =u′·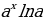 (3) (
(3) ( )′ =u′·
)′ =u′· (2)
(2)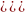 =
=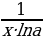 (3)
(3)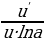 (4)
(4)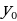
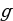 (
(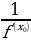
 y=
y= 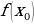 +
+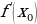 ·(x-
·(x- 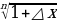 ≈1+
≈1+
 +n
+n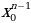 ·△x
·△x ≈
≈ 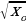 +
+
 ≈1+
≈1+


 onda △ABC △A1 B 1C1
onda △ABC △A1 B 1C1 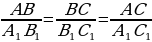 , onda △ABC △A1 B 1C1ч
, onda △ABC △A1 B 1C1ч 



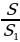 =
= 
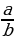


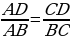













 So.pr=S·cosφ
So.pr=S·cosφ 



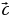 = х
= х 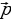 = х
= х 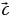 (3)
(3) +y
+y + z
+ z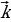 (4)
(4) 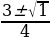 ; X1=1, X2 =
; X1=1, X2 = 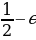 deň bolan iki sany köki bar.
deň bolan iki sany köki bar. 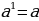 (6)
(6)

















