§2. Математикалык логика боюнча негизги түшүнүктөр. Көптүктөр теориясы.
Логика сөзү гректердин “logos- сөз, ой ,кеп, акыл” деген сөзүнөн алынып, логика илими ой жүгүртүү менен туура чечим кабыл алуу усулдары жана мыйзамдары жөнүндөгү илим болот. Ал үч бөлүктөн турат: диалектикалык логика, математикалык логика жана формалдуу логика.
Диалектикалык логика – адамдын ой жүгүртүүсүндө объективдүү дүйнөнүн турпатын чагылуу абалы жана чындыкты таанып – билүүнүн мыйзам ченемдери жөнүндөгү илим. Анын элементтерин байыркы Гераклит, Платон, Аристотель ж. б. ойчулдардын эмгектеринде, ал эми таанып-билүүнүн, ой жүгүртүүнүн жалпы принциптери жана методдору боюнча Ф. Бекон, Декарт, Лейбниц ж. б. окууларында жолуктурууга болот. Диалектикалык логиканы өнүктүрүүгө Кант менен Гегель белгилүү салым кошушкан. Анын негизги маселеси катары, заттардын кыймыл аракетин, диалектиканын мыйзамдары аркылуу түшүнүктөрдө чагылдырууну изилдөө, анын негизинде ой жүгүртүүнүн өзүнүн өнүгүшүн үйрөнүү, таанып – билүүнүн жалпы мыйзам ченемдери болуп эсептелет.
Формалдуу логика – ойдун формаларынын (ойдо талдоо, ой жыйынтыктоо, түшүнүү, далилдөө ж. б.) логикалык түзүлүшүн үйрөтүүчү илим. Формалдуу логиканын негизги максаты – корутунду билимге ээ болуу жараянында сакталуучу мыйзамдарды жана принциптерди иштеп чыгуу болуп саналат.
Математикалык логика – математиканын формалдуу методдорун жана математикалык ой жүгүртүүлөр менен далилдөөлөрдүн, логикалык изилдөөлөрдү колдонуунун натыйжасында түзүлгөн билимдер тармагы. Математикалык логикада: логикалык процесстер – логикалык эсептөөлөр сыяктуу формалдаштырылган тилдерде, аларды чагылдыруу аркылуу изилденет. Логикалык эсептөөлөрдүн формалдуу түзүлүшүн изилдөө менен катар эле, эсептөөлөр жана алардын интерпретациясы менен моделдери болуп кызмат кылуучу мазмундуу тармактардын ортосундагы катыш – байланыштарды кароо милдети да турат.
Математикалык логиканын изилдөө ыкмаларында математикалык тамга – символдор, сөз – сүйлөмдөр менен кошо, логиканын өзүнүн символдордон куралган тили колдонулат. Логиканын негизги түшүнүктөрүн бирин “Айтуу” дейбиз.
Def – 1. Логикада чын же жалган деп бир мааниде мүнөздөөгө мүмкүн болгон жай сүйлөмдү - “Айтуу” деп атайбыз.
Демек “Айтуу” бир учурда чын жана жалган боло албайт. Мисалы: “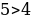 ” - чын айтуу; “Мугалим пара албайт” – айтуу эмес; “
” - чын айтуу; “Мугалим пара албайт” – айтуу эмес; “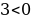 ” – жалган айтуу; “
” – жалган айтуу; “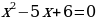 ” - айтуу эмес.
” - айтуу эмес.
Аныктамада айтылгандай суроолуу, илептүү сүйлөмдөр айтуу боло албайт. Логикада айтууларды кичине тамгалар менен белгилеп жазып, анын мазмунуна эмес чын же жалган экендигине гана маани берилип, айтуулардын арасындагы катыш – байланыштары изилденет. Айтуулар чын болсо “1”, жалган болсо “0” сандары менен бааланышат.
Математикалык логикада “Айтууларды” толук изилдөө системасы “предикаттар логикасы” аркылуу толукталат. Өзгөрүлмө чоңдуктар катышкан сүйлөмдү – “предикат” деп атайбыз. Предикат өзгөрүлмөлөрдүн ар башка маанилеринде “чын” же “жалган” маанилерди кабыл алышы мүмкүн.
Мисалы 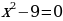 - сүйлөмү предикат болот. Ал өзгөрүлмөлөрдүн
- сүйлөмү предикат болот. Ал өзгөрүлмөлөрдүн 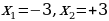 маанилеринде “чын”, ал эми калган маанилерде “жалган” айтуулар болушат.
маанилеринде “чын”, ал эми калган маанилерде “жалган” айтуулар болушат.
Жогоруда §1 де баяндалган математикалык тамга – белгилер жана кийинки логикалык символдордун баары, реалдуу дүйнөдө жашабаган, кыялыбызда гана формалдуу белгиленген түзүлүштөр болушат. Математикалык логиканын бүгүнкү милдети: кыялыбызда кабыл алган формалдуу символдорду, кыялыбызда киргизилген амалдар аркылуу байланыштырып, реалдуу дүйнө процесстерин математикалык моделдерин түзүп, моделдер аркылуу туура чечимдерди кабыл алуу усулдарын изилдөө болуп эсептелет.
Көптүктөр теориясы
Математикадагы «натуралдык сан», «чекит», «түз сызык», «аралык» ж. б. алгачкы түшүнүктөр сыяктуу «көптүк» түшүнүгү да алгачкы түшүнүк болуп, ага аныктоо берилбейт жана мисалдар келтирүү менен түшүндүрүүгө болот. Көптүктөр теориясын аксиомалардын жардамы менен да түзүүгө болот.
Көптүктөр теориясы учурдагы математиканын негиздерин бири болуп, анын теориялык негиздери Георг Кантор (1845—1918) тарабынан 1872-жылы берилген. Кантордун теориясы боюнча «көптүк - бул бир жерге чогултулган элес» болот. Мисалы, класстагы окуучулардын көптүгү, кыргыз алфавитиндеги тамгалардын көптүгү, библиотекадагы китептердин көптүгү, А чекити аркылуу өтүүчү түз сызыктардын көптүгү, 5 цифрасын камтып турган эки орундуу сандардын көптүгү, 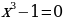 теңдемесинин тамырларынын көптүгү, ж. б. Жалпысынан алганда кандайдыр жалпы касиетке ээ болгон объектилердин, нерселердин тобу же биригүүсү көптүк болот. Турмушта «көптүк» сөзүнүн маанисин билдирүүчү башка сөздөр да колдонулат. Алар: «ансамбль», «коллекция», «армия», «букет», «система», «парк» ж. б. сөздөрү – көптүк сөзүнүн синонимдери болушат. Мисалы, бир нече комузчулардын тобу комузчулардын ансамблин, бир топ гүлдөр букетти түзүшөт, бир нече трактор турган жер тракторлордун паркы деп аталат. Көптүктөр А, В, С, D,... ,Х, У,... сыяктуу чоң тамгалар менен белгиленет. Көптүккө кирген объектилер, нерселер анын элементтери деп аталышат.
теңдемесинин тамырларынын көптүгү, ж. б. Жалпысынан алганда кандайдыр жалпы касиетке ээ болгон объектилердин, нерселердин тобу же биригүүсү көптүк болот. Турмушта «көптүк» сөзүнүн маанисин билдирүүчү башка сөздөр да колдонулат. Алар: «ансамбль», «коллекция», «армия», «букет», «система», «парк» ж. б. сөздөрү – көптүк сөзүнүн синонимдери болушат. Мисалы, бир нече комузчулардын тобу комузчулардын ансамблин, бир топ гүлдөр букетти түзүшөт, бир нече трактор турган жер тракторлордун паркы деп аталат. Көптүктөр А, В, С, D,... ,Х, У,... сыяктуу чоң тамгалар менен белгиленет. Көптүккө кирген объектилер, нерселер анын элементтери деп аталышат.
Көптүктүн элементтери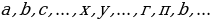 сыяктуу кичине тамгалар менен белгиленишет. Эгерде а объектиси А көптүгүнүн элементи болсо,
сыяктуу кичине тамгалар менен белгиленишет. Эгерде а объектиси А көптүгүнүн элементи болсо, 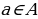 деп жазылат жана «
деп жазылат жана « 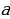 элементи А көптүгүнө таандык» деп окулат. Эгерде
элементи А көптүгүнө таандык» деп окулат. Эгерде 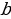 элементи А көптүгүнүн элементи болбосо, ал
элементи А көптүгүнүн элементи болбосо, ал 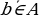 деп жазылат жана «
деп жазылат жана «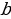 элементи А көптүгүнө таандык эмес» деп окулат. Мисалы, А жуп сандардын көптүгү болсо, анда 102
элементи А көптүгүнө таандык эмес» деп окулат. Мисалы, А жуп сандардын көптүгү болсо, анда 102 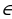 А болот, бирок 13
А болот, бирок 13 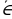 А. Бир да элементи жок болгон көптүк бош же куру көптүк деп аталып
А. Бир да элементи жок болгон көптүк бош же куру көптүк деп аталып 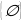 - символу менен белгиленет.
- символу менен белгиленет.
Сандардын алгебрасында сандар менен түрдүүчө амалдарды жүргүзгөндөй эле, көптүктөр менен да бир топ алгебралык амалдарды жүргүзүүгө болот.
1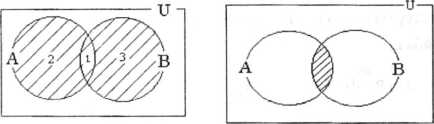 . Көптүктөрдү кошуу
. Көптүктөрдү кошуу
а) 1 – чийме б)
Def – 2. Эгерде А,В,С, ... , D көптуктөрү берилген болсо, анда жок дегенде алардын бирине таандык болгон элементтердин көптүгү, ал көптүктөрдүн суммасы (биригүүсү) деп аталат жана ал
А В
В С
С ...
...  D символу менен белгиленет (“
D символу менен белгиленет (“ ” – биригүү белгиси).
” – биригүү белгиси).
Эгерде А=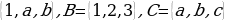 болсо , анда
болсо , анда
А В
В С=
С= 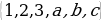 болот. А – жуп сандардын көптүгү, В – так сандардын көптүгү болсо, анда А
болот. А – жуп сандардын көптүгү, В – так сандардын көптүгү болсо, анда А В баардык жуп жана так сандардын көптүгү болот.
В баардык жуп жана так сандардын көптүгү болот. 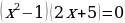 теңдемесин чыгаруу талап кылынсын дейли. Анда ал барабардыкты канааттандыруучу
теңдемесин чыгаруу талап кылынсын дейли. Анда ал барабардыкты канааттандыруучу
М=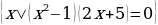 көптүктүн элементтерин табуу жетиштүү. Ал
көптүктүн элементтерин табуу жетиштүү. Ал
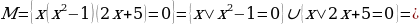
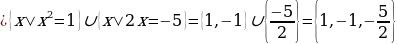 көптүгү болот. Бул көптүктүн каалаган элементи берилген теңдеменин чыгарылышы болот. Аны ордуна коюп текшерүү мүмкүн.
көптүгү болот. Бул көптүктүн каалаган элементи берилген теңдеменин чыгарылышы болот. Аны ордуна коюп текшерүү мүмкүн.
Эки А, В көптүктөрүн биригүүсүн 1а) – чиймеде штрихтелип көрсөтүлгөн. Мында  универсалдык көптүк деп аталып, ал бардык көптүктөрдү камтып турган кудреттүү көптүк катары эсептелет.
универсалдык көптүк деп аталып, ал бардык көптүктөрдү камтып турган кудреттүү көптүк катары эсептелет.
Көптүктөрдү кошуунун аныктамасынан төмөнкү касиеттер келтирилип чыгарылат:
А ( кошуунун орун алмаштыруу закону);
( кошуунун орун алмаштыруу закону);
(А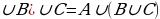 ( топтоштуруу закону);
( топтоштуруу закону);
А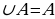 ;
;
А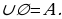 Мында
Мында 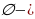 элементи жок “бош” же “куру” көптүк.
элементи жок “бош” же “куру” көптүк.
2 . Көптүктөрдү көбөйтүү
Def – 3. Бизге А жана В көптүктөрү берилсе, анда алардын экөөсүнө тең таандык болгон элементтердин көптүгү, А жана В көптүктөрүнүн көбөйтүндүсү (кесилиши) деп аталат жана ал 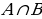 символу менен белгиленет :
символу менен белгиленет : 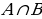 =
= 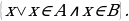
Эгерде А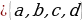 , B
, B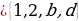 болсо, анда
болсо, анда 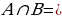
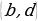 болот. Эгерде А – тик бурчтуктардын көптүгү, В – ромбдордун көптүгү болсо, анда
болот. Эгерде А – тик бурчтуктардын көптүгү, В – ромбдордун көптүгү болсо, анда 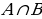 – квадраттардын көптүгү болот. А=
– квадраттардын көптүгү болот. А=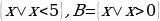 болсо, анда
болсо, анда 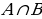 =
=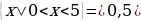 интервалы болот. Эгерде А жана В көптүктөрү жалпы элементтерге ээ болушпаса, анда алардын кесилиши куру
интервалы болот. Эгерде А жана В көптүктөрү жалпы элементтерге ээ болушпаса, анда алардын кесилиши куру 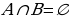 көптүк болот. Мисалы, А=
көптүк болот. Мисалы, А=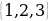 , В=
, В=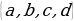 болсо, анда
болсо, анда 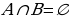 . Эгерде
. Эгерде 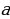 түз сызыгы жана
түз сызыгы жана 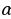 тегиздиги өз ара параллель болушса, анда
тегиздиги өз ара параллель болушса, анда 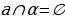 болот, ж.у.с. Эки А, В көптүктөрдүн кесилиши 1б)– чиймеде штрихтелип көрсөтүлгөн.
болот, ж.у.с. Эки А, В көптүктөрдүн кесилиши 1б)– чиймеде штрихтелип көрсөтүлгөн.
Көптүктөрдү көбөйтүүнүн аныктамасынан төмөнкүдөй натыйжалар келип чыгат.
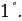 Ар дайым
Ар дайым 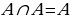 , жалпысынан алганда
, жалпысынан алганда 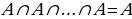 болот.
болот.
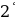 .
. 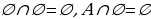 ;
;
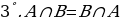 ;
;
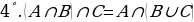 ;
;
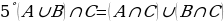 .
.
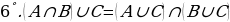 .
.
А көптүгүн тануусу деп, анын элементтерин танган маанидеги (карама – каршы же тескери) элементтердин көптүгүн айтып, тануу көптүгүн 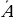 символу менен белгилейбиз. Мисалы
символу менен белгилейбиз. Мисалы 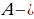 бардык так натуралдык сандардын көптүгү болсо,
бардык так натуралдык сандардын көптүгү болсо, 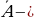 бардык так эмес же жуп натуралдык сандардын көптүгү болот. 2 б) – чиймеде А көптүгүн
бардык так эмес же жуп натуралдык сандардын көптүгү болот. 2 б) – чиймеде А көптүгүн 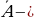 тануусу штрихтелип көрсөтүлгөн.
тануусу штрихтелип көрсөтүлгөн.
Көптүктөрдү кошууда жана көбөйтүүдө де Моргандын закону деп аталуучу төмөнкү байланыш – катышы орун алат:
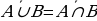 , (1)
, (1)
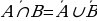 . (2)
. (2)
Акырында төмөнкү туура барабардыктарды эске сала кетебиз:
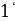 .
.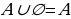 ;
; 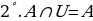 ;
; 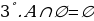 ;
; 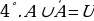 ;
;

а) 2 – чийме б)
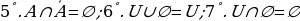 .
.
3. Көптүктөрдү кемитүү
Def – 4. А жана В көптүктөрү берилсин. В көптүгүнө таандык болбогон А көптүгүн элементтеринин көптүгү, А жана В көптүктөрүнүн айырмасы деп аталат жана 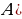 символу менен белгиленет (2а - чийме).
символу менен белгиленет (2а - чийме).
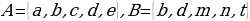 болсо,
болсо, 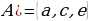 болот. Жалпы эле
болот. Жалпы эле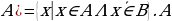 — натуралдык сандардын көптүгү, В — жөнөкөй сандарын көптүгү болсо, анда
— натуралдык сандардын көптүгү, В — жөнөкөй сандарын көптүгү болсо, анда 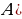 — бир саны менен бардык курама сандардын көптүгү болот.
— бир саны менен бардык курама сандардын көптүгү болот.
A көптүгү берилсе 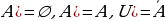 экендигин айта кетүү зарыл. Эгерде
экендигин айта кетүү зарыл. Эгерде 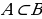 болсо,
болсо, 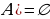 болот.
болот.
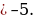 В нын элементи болбогон А көптүгүнүн элементтери менен, А нын элементи болбогон В көптүгүн элементеринин суммасы, А жана В көптүктөрүн симметриялуу айырмасы деп аталат жана ал айырма
В нын элементи болбогон А көптүгүнүн элементтери менен, А нын элементи болбогон В көптүгүн элементеринин суммасы, А жана В көптүктөрүн симметриялуу айырмасы деп аталат жана ал айырма 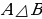 символу менен белгиленет.
символу менен белгиленет.
Аныктаманы белгилер менен 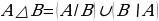 көрүнүштө жазып, симметриялуу айырманы
көрүнүштө жазып, симметриялуу айырманы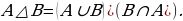 деп да жазабыз.
деп да жазабыз.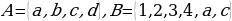 болсо, анда
болсо, анда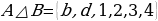 болот.
болот. 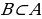 болсо, анда
болсо, анда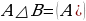 , ал эми
, ал эми
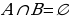 болсо,
болсо, 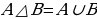 болот, ж. у. с.
болот, ж. у. с.
Практикада изилдөө зарылдыгына жараша, ар кандай нерселердин көптүктөрү каралганы менен, аларды изилдөө ыкмалары сандарга салыштырылып жүргүзүлөт. Ошондуктан, математика илиминде сандык көптүктөр же сан тамгалардын көптүктөрү кеңири колдонулуп, өзгөчө орунда турат.








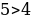 ” - чын айтуу; “Мугалим пара албайт” – айтуу эмес; “
” - чын айтуу; “Мугалим пара албайт” – айтуу эмес; “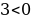 ” – жалган айтуу; “
” – жалган айтуу; “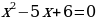 ” - айтуу эмес.
” - айтуу эмес.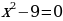 - сүйлөмү предикат болот. Ал өзгөрүлмөлөрдүн
- сүйлөмү предикат болот. Ал өзгөрүлмөлөрдүн 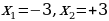 маанилеринде “чын”, ал эми калган маанилерде “жалган” айтуулар болушат.
маанилеринде “чын”, ал эми калган маанилерде “жалган” айтуулар болушат.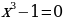 теңдемесинин тамырларынын көптүгү, ж. б. Жалпысынан алганда кандайдыр жалпы касиетке ээ болгон объектилердин, нерселердин тобу же биригүүсү көптүк болот. Турмушта «көптүк» сөзүнүн маанисин билдирүүчү башка сөздөр да колдонулат. Алар: «ансамбль», «коллекция», «армия», «букет», «система», «парк» ж. б. сөздөрү – көптүк сөзүнүн синонимдери болушат. Мисалы, бир нече комузчулардын тобу комузчулардын ансамблин, бир топ гүлдөр букетти түзүшөт, бир нече трактор турган жер тракторлордун паркы деп аталат. Көптүктөр А, В, С, D,... ,Х, У,... сыяктуу чоң тамгалар менен белгиленет. Көптүккө кирген объектилер, нерселер анын элементтери деп аталышат.
теңдемесинин тамырларынын көптүгү, ж. б. Жалпысынан алганда кандайдыр жалпы касиетке ээ болгон объектилердин, нерселердин тобу же биригүүсү көптүк болот. Турмушта «көптүк» сөзүнүн маанисин билдирүүчү башка сөздөр да колдонулат. Алар: «ансамбль», «коллекция», «армия», «букет», «система», «парк» ж. б. сөздөрү – көптүк сөзүнүн синонимдери болушат. Мисалы, бир нече комузчулардын тобу комузчулардын ансамблин, бир топ гүлдөр букетти түзүшөт, бир нече трактор турган жер тракторлордун паркы деп аталат. Көптүктөр А, В, С, D,... ,Х, У,... сыяктуу чоң тамгалар менен белгиленет. Көптүккө кирген объектилер, нерселер анын элементтери деп аталышат.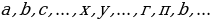 сыяктуу кичине тамгалар менен белгиленишет. Эгерде а объектиси А көптүгүнүн элементи болсо,
сыяктуу кичине тамгалар менен белгиленишет. Эгерде а объектиси А көптүгүнүн элементи болсо, 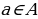 деп жазылат жана «
деп жазылат жана « 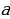 элементи А көптүгүнө таандык» деп окулат. Эгерде
элементи А көптүгүнө таандык» деп окулат. Эгерде 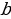 элементи А көптүгүнүн элементи болбосо, ал
элементи А көптүгүнүн элементи болбосо, ал 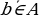 деп жазылат жана «
деп жазылат жана «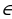 А болот, бирок 13
А болот, бирок 13 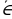 А. Бир да элементи жок болгон көптүк бош же куру көптүк деп аталып
А. Бир да элементи жок болгон көптүк бош же куру көптүк деп аталып 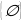 - символу менен белгиленет.
- символу менен белгиленет.  . Көптүктөрдү кошуу
. Көптүктөрдү кошуу 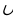 В
В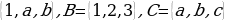 болсо , анда
болсо , анда 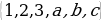 болот. А – жуп сандардын көптүгү, В – так сандардын көптүгү болсо, анда А
болот. А – жуп сандардын көптүгү, В – так сандардын көптүгү болсо, анда А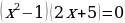 теңдемесин чыгаруу талап кылынсын дейли. Анда ал барабардыкты канааттандыруучу
теңдемесин чыгаруу талап кылынсын дейли. Анда ал барабардыкты канааттандыруучу 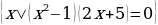 көптүктүн элементтерин табуу жетиштүү. Ал
көптүктүн элементтерин табуу жетиштүү. Ал 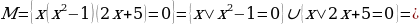
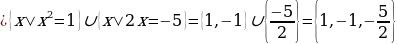 көптүгү болот. Бул көптүктүн каалаган элементи берилген теңдеменин чыгарылышы болот. Аны ордуна коюп текшерүү мүмкүн.
көптүгү болот. Бул көптүктүн каалаган элементи берилген теңдеменин чыгарылышы болот. Аны ордуна коюп текшерүү мүмкүн.  универсалдык көптүк деп аталып, ал бардык көптүктөрдү камтып турган кудреттүү көптүк катары эсептелет.
универсалдык көптүк деп аталып, ал бардык көптүктөрдү камтып турган кудреттүү көптүк катары эсептелет. ( кошуунун орун алмаштыруу закону);
( кошуунун орун алмаштыруу закону); 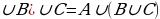 ( топтоштуруу закону);
( топтоштуруу закону);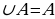 ;
;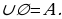 Мында
Мында 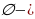 элементи жок “бош” же “куру” көптүк.
элементи жок “бош” же “куру” көптүк.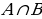 символу менен белгиленет :
символу менен белгиленет : 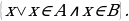
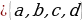 , B
, B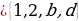 болсо, анда
болсо, анда 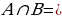
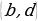 болот. Эгерде А – тик бурчтуктардын көптүгү, В – ромбдордун көптүгү болсо, анда
болот. Эгерде А – тик бурчтуктардын көптүгү, В – ромбдордун көптүгү болсо, анда 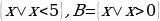 болсо, анда
болсо, анда 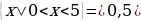 интервалы болот. Эгерде А жана В көптүктөрү жалпы элементтерге ээ болушпаса, анда алардын кесилиши куру
интервалы болот. Эгерде А жана В көптүктөрү жалпы элементтерге ээ болушпаса, анда алардын кесилиши куру 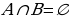 көптүк болот. Мисалы, А=
көптүк болот. Мисалы, А=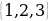 , В=
, В=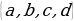 болсо, анда
болсо, анда 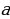 түз сызыгы жана
түз сызыгы жана 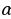 тегиздиги өз ара параллель болушса, анда
тегиздиги өз ара параллель болушса, анда 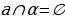 болот, ж.у.с. Эки А, В көптүктөрдүн кесилиши 1б)– чиймеде штрихтелип көрсөтүлгөн.
болот, ж.у.с. Эки А, В көптүктөрдүн кесилиши 1б)– чиймеде штрихтелип көрсөтүлгөн.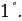 Ар дайым
Ар дайым 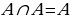 , жалпысынан алганда
, жалпысынан алганда 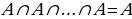 болот.
болот. 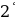 .
. 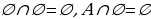 ;
;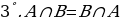 ;
;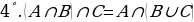 ;
;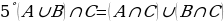 .
.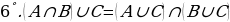 .
.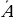 символу менен белгилейбиз. Мисалы
символу менен белгилейбиз. Мисалы 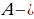 бардык так натуралдык сандардын көптүгү болсо,
бардык так натуралдык сандардын көптүгү болсо, 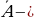 бардык так эмес же жуп натуралдык сандардын көптүгү болот. 2 б) – чиймеде А көптүгүн
бардык так эмес же жуп натуралдык сандардын көптүгү болот. 2 б) – чиймеде А көптүгүн 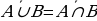 , (1)
, (1)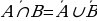 . (2)
. (2)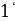 .
.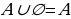 ;
; 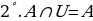 ;
;  ;
; 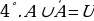 ;
;
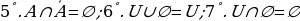 .
. 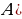 символу менен белгиленет (2а - чийме).
символу менен белгиленет (2а - чийме).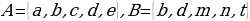 болсо,
болсо, 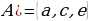 болот. Жалпы эле
болот. Жалпы эле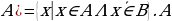 — натуралдык сандардын көптүгү, В — жөнөкөй сандарын көптүгү болсо, анда
— натуралдык сандардын көптүгү, В — жөнөкөй сандарын көптүгү болсо, анда 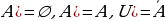 экендигин айта кетүү зарыл. Эгерде
экендигин айта кетүү зарыл. Эгерде 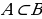 болсо,
болсо, 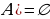 болот.
болот. 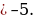 В нын элементи болбогон А көптүгүнүн элементтери менен, А нын элементи болбогон В көптүгүн элементеринин суммасы, А жана В көптүктөрүн симметриялуу айырмасы деп аталат жана ал айырма
В нын элементи болбогон А көптүгүнүн элементтери менен, А нын элементи болбогон В көптүгүн элементеринин суммасы, А жана В көптүктөрүн симметриялуу айырмасы деп аталат жана ал айырма 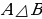 символу менен белгиленет.
символу менен белгиленет.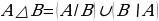 көрүнүштө жазып, симметриялуу айырманы
көрүнүштө жазып, симметриялуу айырманы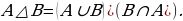 деп да жазабыз.
деп да жазабыз.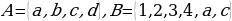 болсо, анда
болсо, анда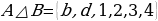 болот.
болот. 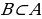 болсо, анда
болсо, анда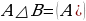 , ал эми
, ал эми 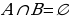 болсо,
болсо, 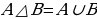 болот, ж. у. с.
болот, ж. у. с.









