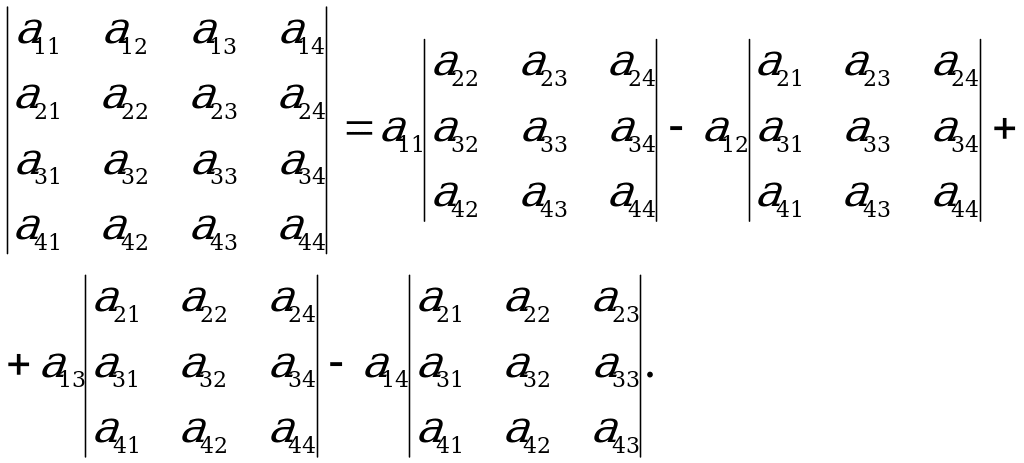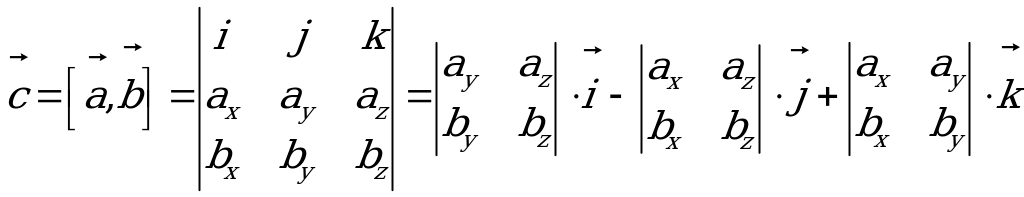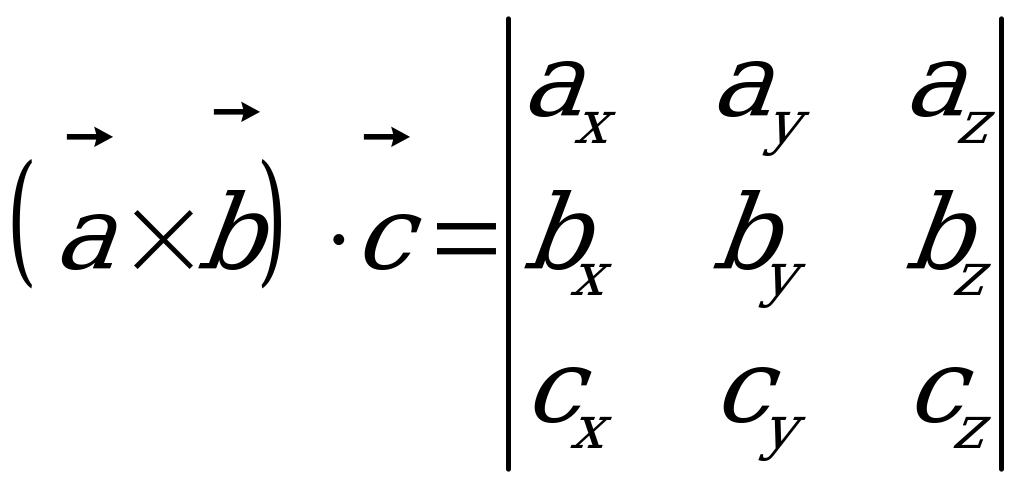MATEMATIKI BELGILEMELER
, – degişli, degişli däl belgileri:
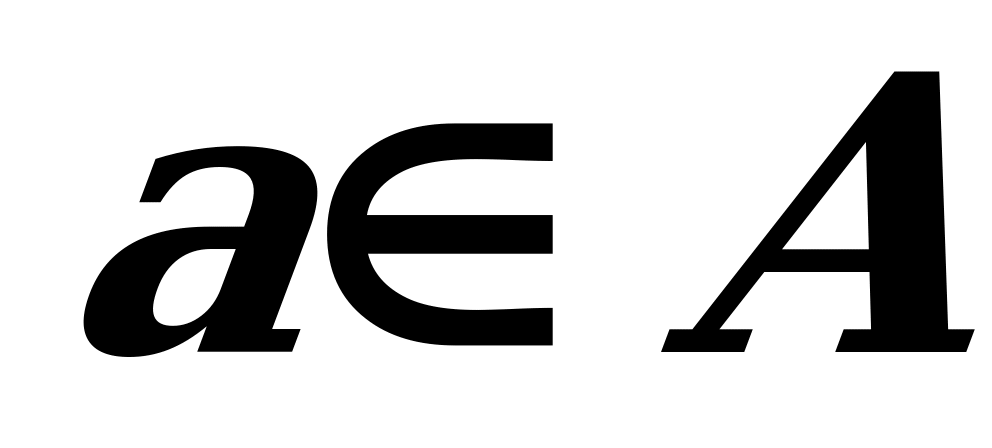 – "a element A köplüge degişli",
– "a element A köplüge degişli", 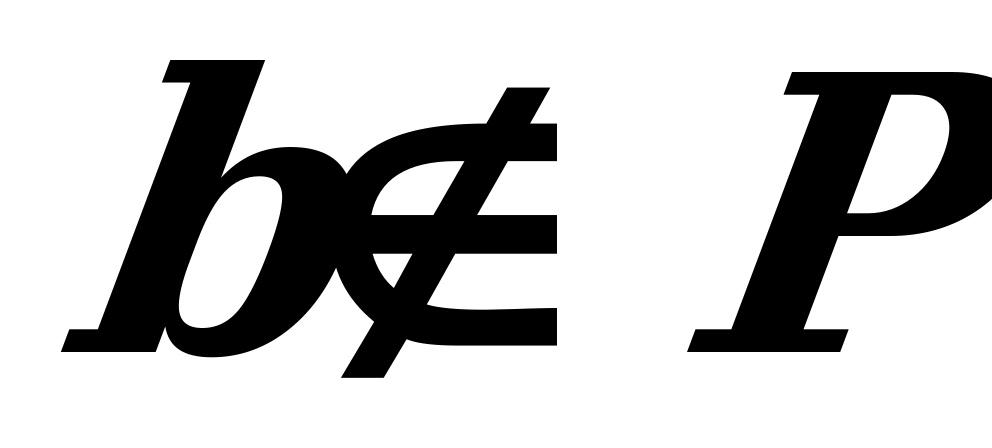 – "b element P köplüge degişli däl" diýlip okalýarlar;
– "b element P köplüge degişli däl" diýlip okalýarlar;
, – girme, özünde saklama belgileri:
BA – "B köplük A köplügine girýär – bölek köplügi",
AB – "A köplük B köplügini (bölek köplügini) özünde saklaýar"
ýaly okalýarlar;
– "islendik … üçin" belgisi:
B – "islendik B köplük üçin" diýlip okalýar;
– "bar", "tapylýar" belgisi:
M – "M köplügi bar",
xR – "R köplügine degişli x element bar, tapylýar" ýaly okaýlarlar;
: – "ýerine ýetýär", "ýerinde bar" belgisi:
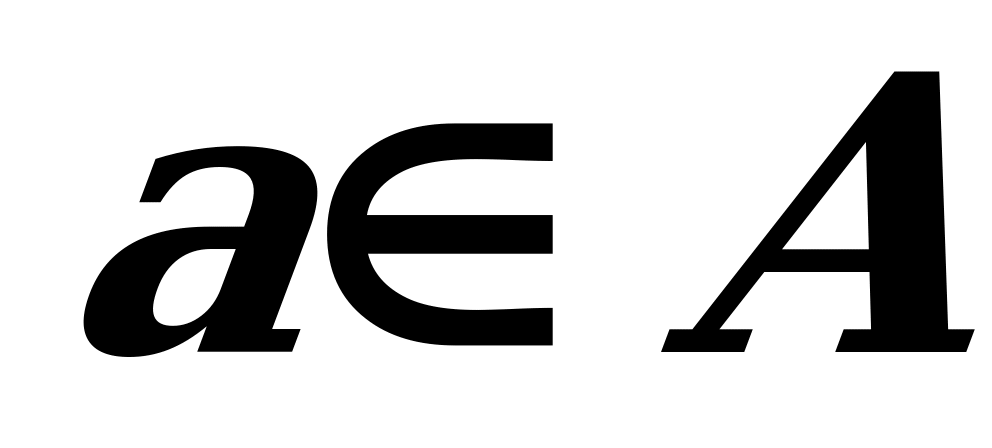 :
:  – "A köplüge degişli islendik a element üçin, a element B köplüge degişlidir" diýlip okalýar;
– "A köplüge degişli islendik a element üçin, a element B köplüge degişlidir" diýlip okalýar;
– "logiki gelip çykmak", "eger… bolsa, onda …" belgisi:
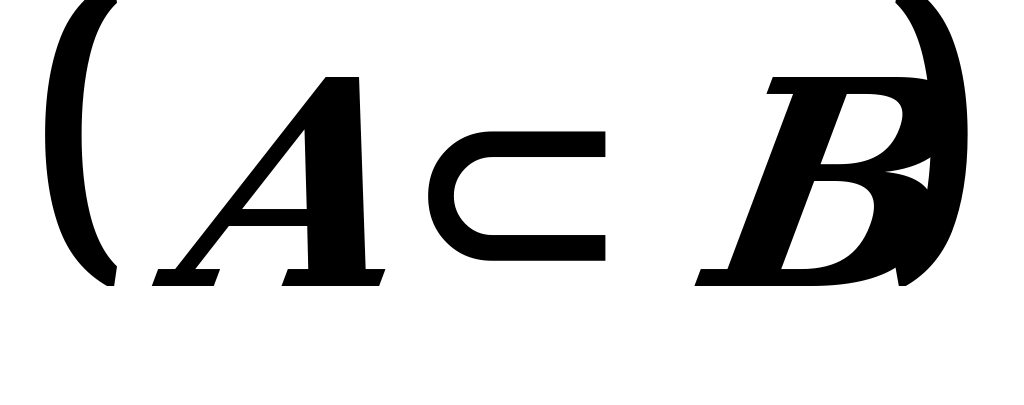 (
(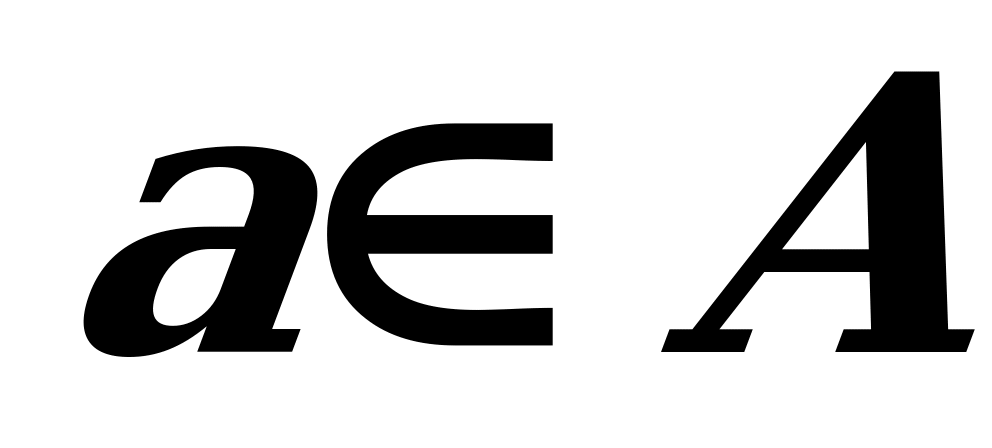 :
: 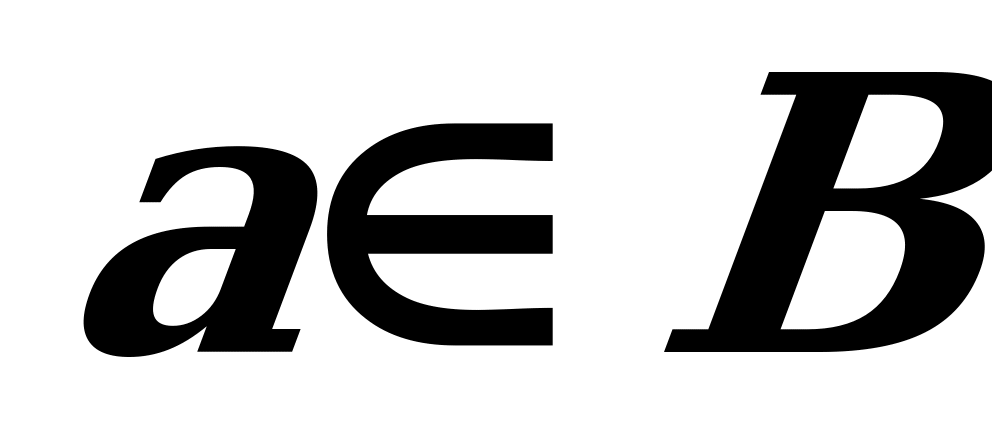 ) – "eger A köplük B köplügiň bölek köplügi bolsa, onda A köplügiň islendik a elementi üçin a degişli B gelip çykýar" diýlip okalýär.
) – "eger A köplük B köplügiň bölek köplügi bolsa, onda A köplügiň islendik a elementi üçin a degişli B gelip çykýar" diýlip okalýär.
7.  - "deňgüýçlilik", "şonda we diňe şonda, haçanda" belgisi:
- "deňgüýçlilik", "şonda we diňe şonda, haçanda" belgisi:  - "P tassyklama Q tassyklama deňgüýçli" ýa-da "P tassyklama ýerine ýetýär, şonda we diňe şonda, haçanda Q ýerine ýetende", ýa-da "P tassyklamadan Q gelip çykýär we tersine , Q tassyklamadan P gelip çykýär" diýlip okalýar.
- "P tassyklama Q tassyklama deňgüýçli" ýa-da "P tassyklama ýerine ýetýär, şonda we diňe şonda, haçanda Q ýerine ýetende", ýa-da "P tassyklamadan Q gelip çykýär we tersine , Q tassyklamadan P gelip çykýär" diýlip okalýar.
Şu bellemeleri girizmek bilen, meselem,
görnüşlerde ýazmak bolar.
KESGITLEÝJILERIŇ HASAPLANYŞY
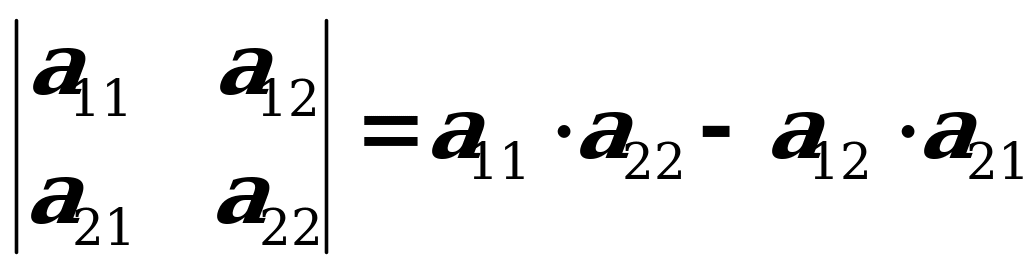
 .
.
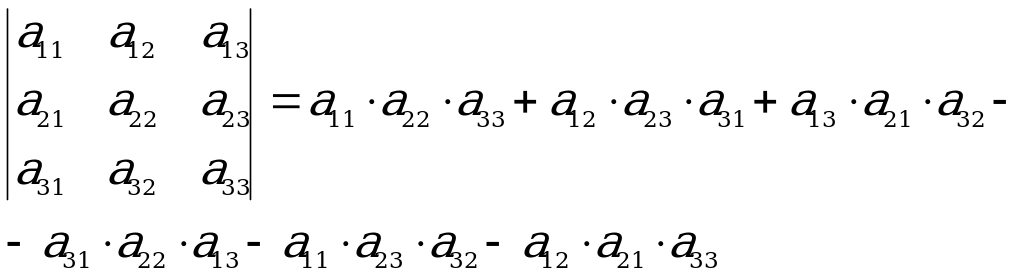
Üçünji tertipli kesgitleýjini hasaplamakda aşakdaky shemany ulanmak amatlydyr:
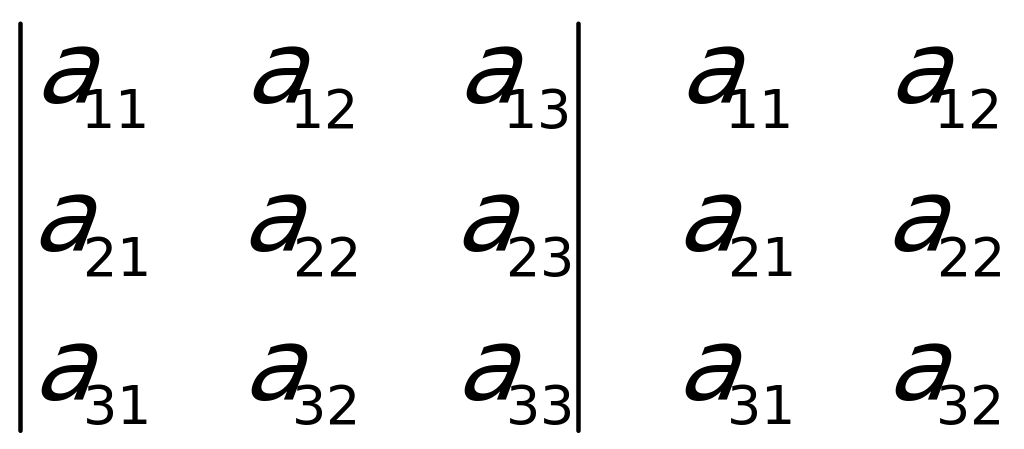
 .
.  .
.
Kesgitleýjini i-nji setiriň elementleri boýunça dargadyp, şeýle ýazmak bolar:
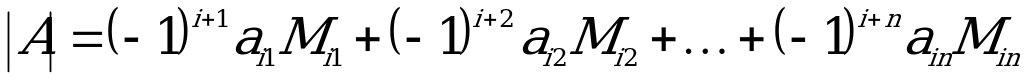 ,
,
bu ýerde  arkaly
arkaly  matrisanyň i-nji setirini we j-nji sütünini çyzmakdan galýan (n-1)-nji tertipli kesgitleýji – minor belgilenendir.
matrisanyň i-nji setirini we j-nji sütünini çyzmakdan galýan (n-1)-nji tertipli kesgitleýji – minor belgilenendir.
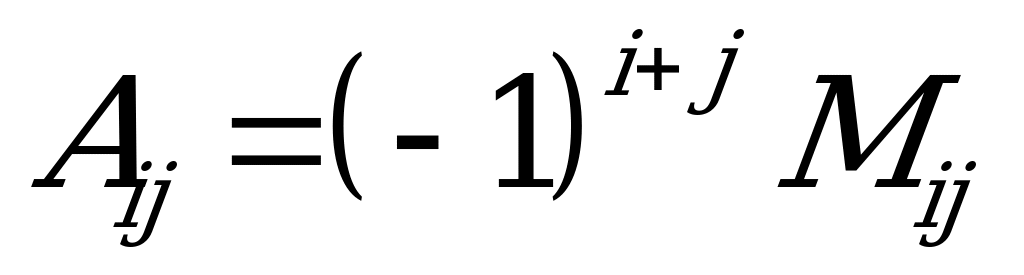 ululyga
ululyga  elementiň algebraik doldurgyjy diýilýär.
elementiň algebraik doldurgyjy diýilýär.
Onda (*) dargatmany şeýle ýazmak bolar:
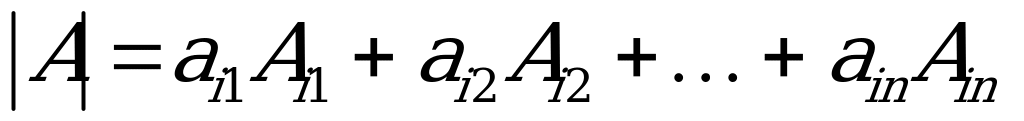 . (**)
. (**)
(**) formula boýunça 4-nji tertipli kesgitleýjini 1-nji setiriň elementleri boýunça dargadyp alarys:
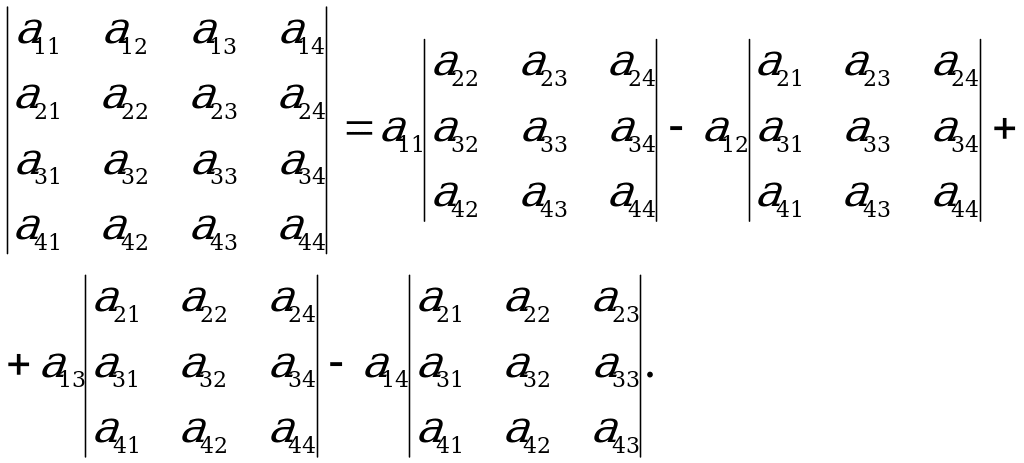
WEKTORLARYŇ SKALÝAR KÖPELTMEK HASYLY
 we
we  wektorlaryň skalýar köpeltmek hasyly şeýle bir c san bolup,
wektorlaryň skalýar köpeltmek hasyly şeýle bir c san bolup, 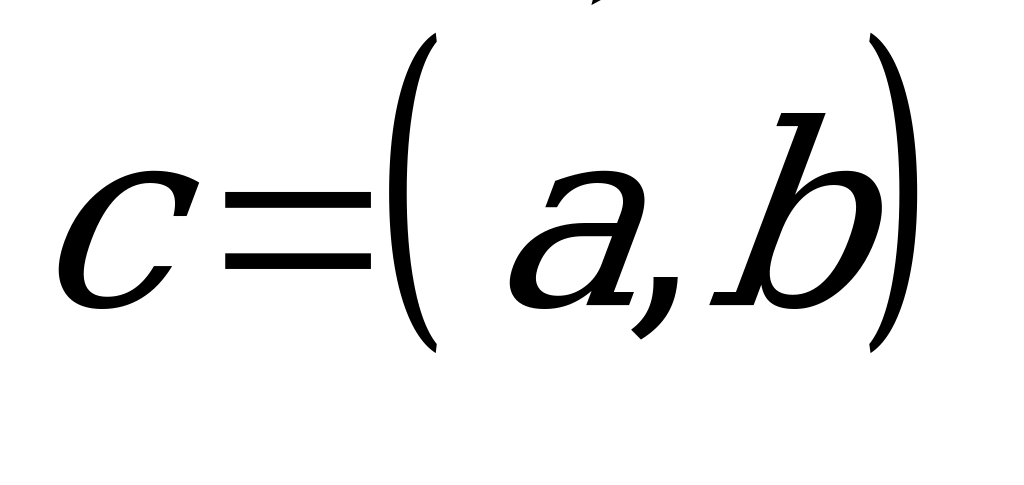 ýa-da
ýa-da 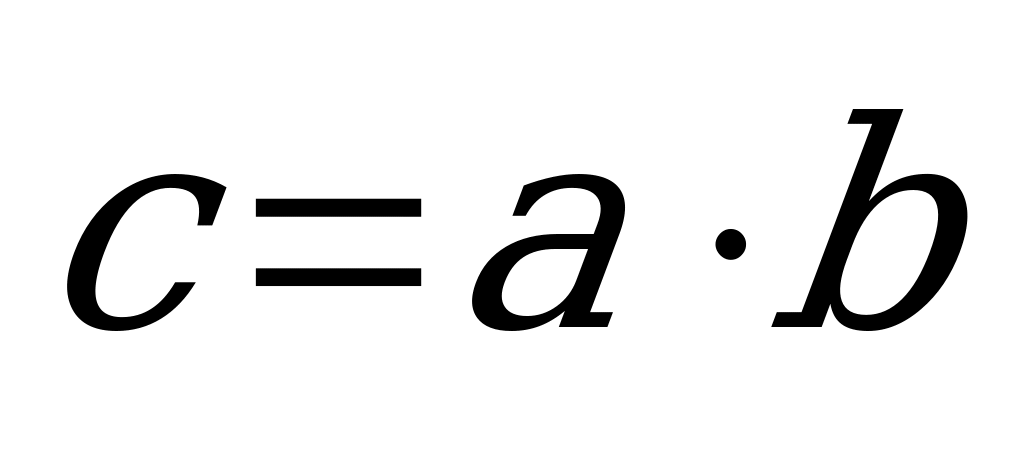 ýaly belgilenilýär we şeýle formula bilen kesgitlenýär:
ýaly belgilenilýär we şeýle formula bilen kesgitlenýär: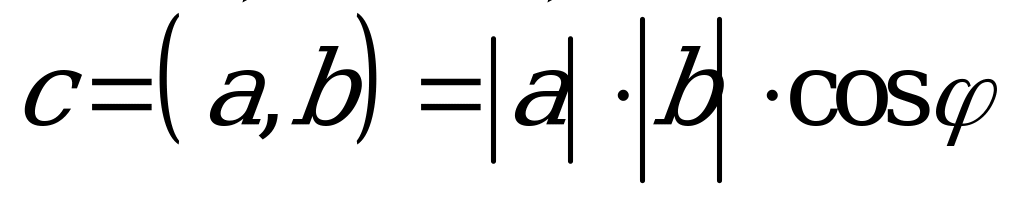 ,bu ýerde –
,bu ýerde – 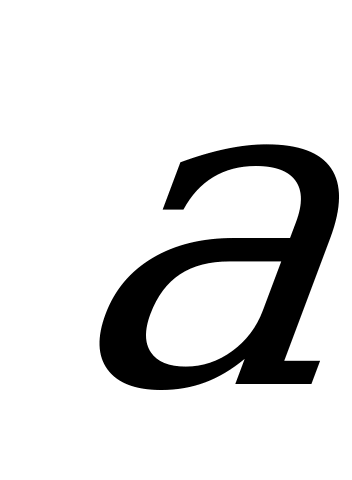 we
we  wektorlaryň arasyndaky burçdur.
wektorlaryň arasyndaky burçdur.
Wektoryň öz-özüne skalýar köpeltmek hasyly onuň modulynyň kwadratyna deňdir: 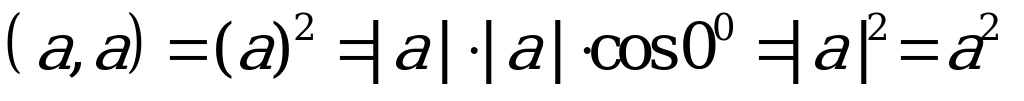 .
.
Eger wektorlar gönüburçly koordinatlar tekizliginde
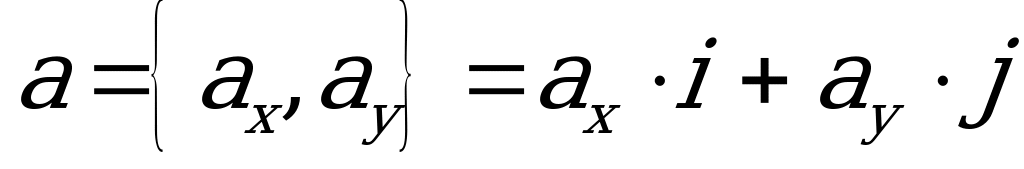 ,
, 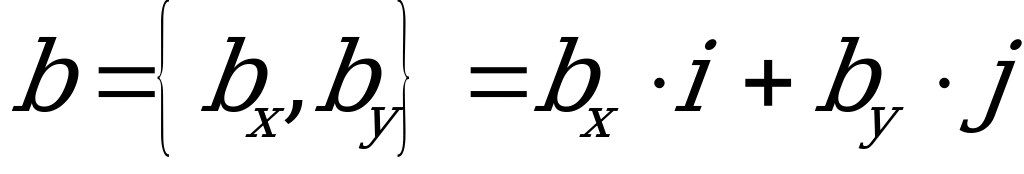
koordinatlary bilen berlen bolsalar, onda olaryň skalýar köpeltmek hasyly 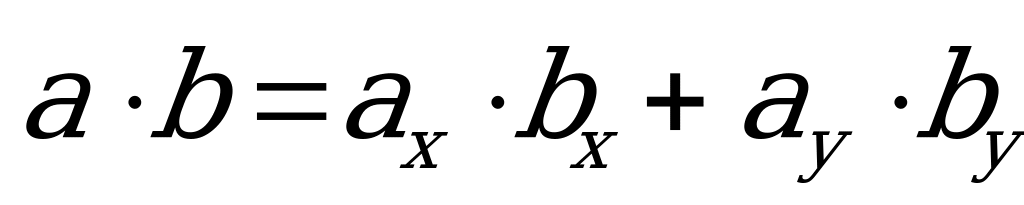 .
.
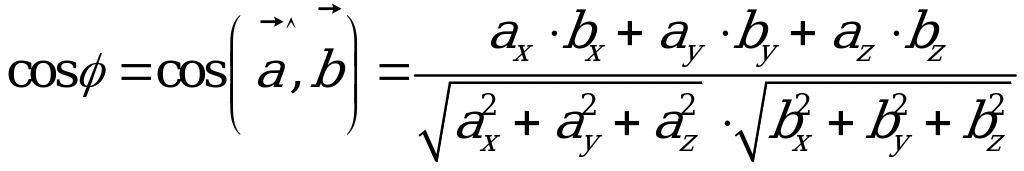 .
.
Berlen  wektor bilen
wektor bilen  ,
,  ,
, 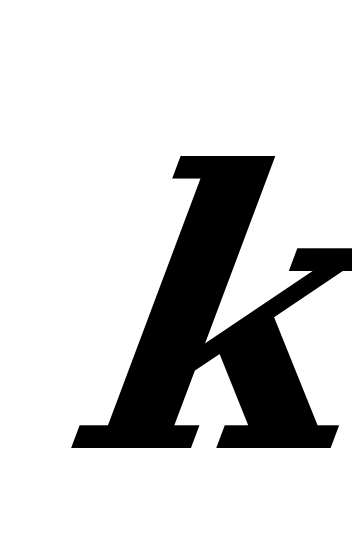 ortlar arasyndaky , , burçlarynyň kosinuslaryna ugrukdyryjy kosinuslar diýilýär we olar şeýle tapylýarlar:
ortlar arasyndaky , , burçlarynyň kosinuslaryna ugrukdyryjy kosinuslar diýilýär we olar şeýle tapylýarlar:
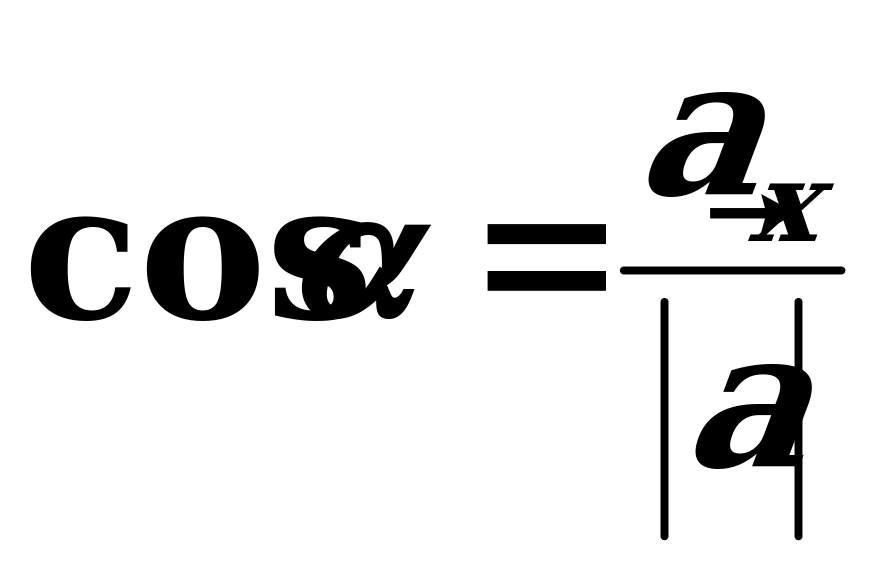 ,
, 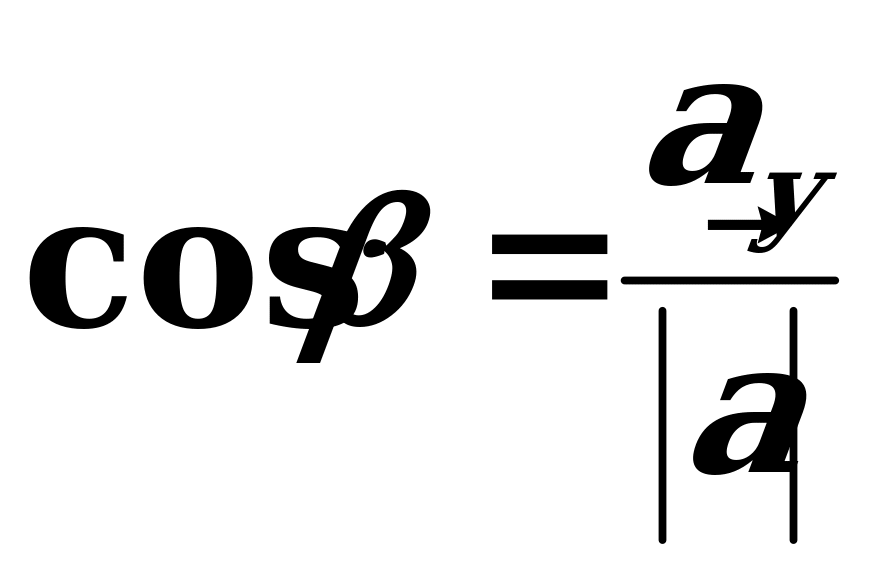 ,
,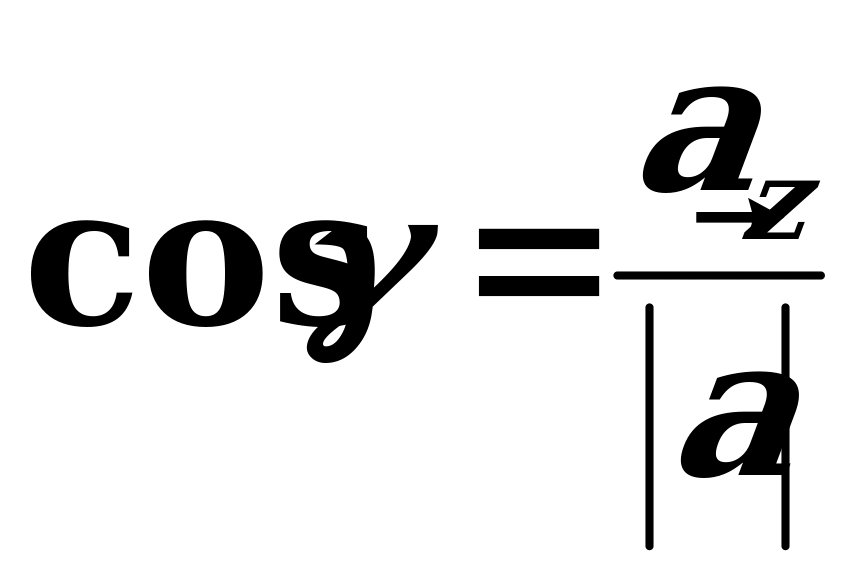 (giňişlikde).
(giňişlikde).
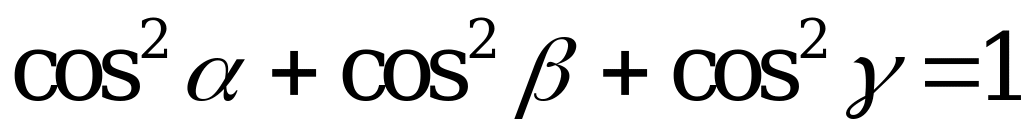 .
.
WEKTORLARYŇ WEKTOR KÖPELTMEK HASYLY
Kesgitleme.  we
we  wektorlaryň wektor köpeltmek hasyly şeýle bir
wektorlaryň wektor köpeltmek hasyly şeýle bir  wektor bolup,
wektor bolup, 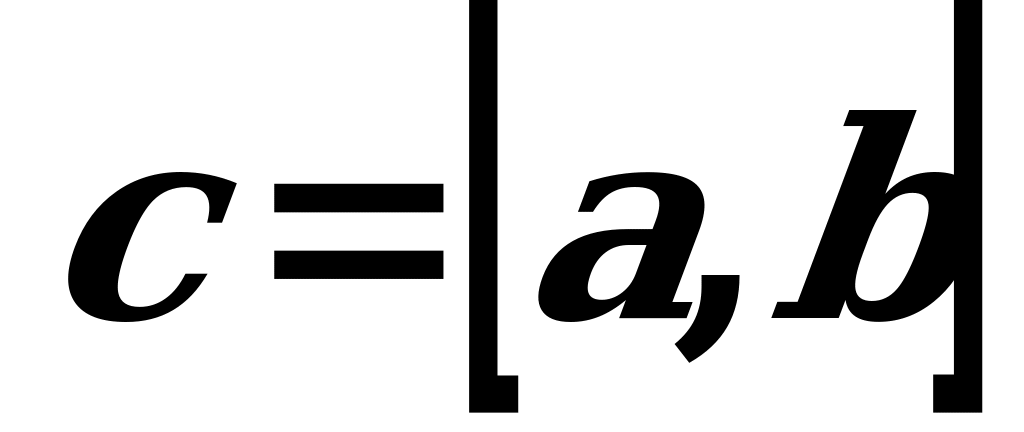 ýa-da
ýa-da 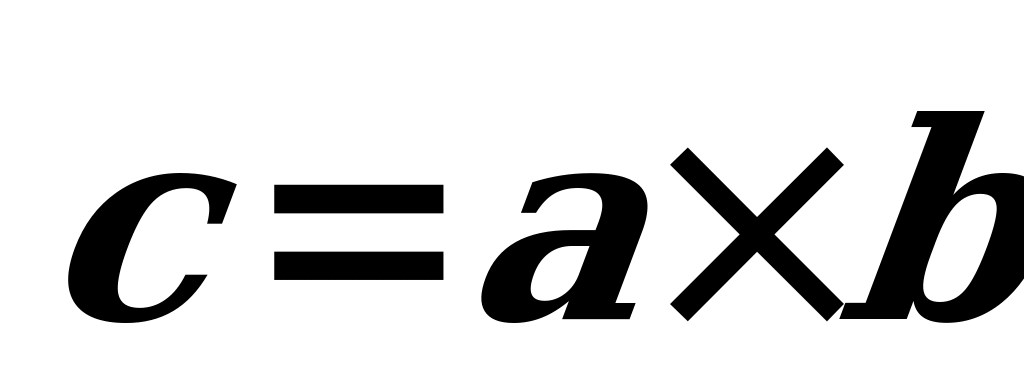 ýaly belgilenilýär we aşakdaky üç şert boýunça kesgitlenýär:
ýaly belgilenilýär we aşakdaky üç şert boýunça kesgitlenýär:
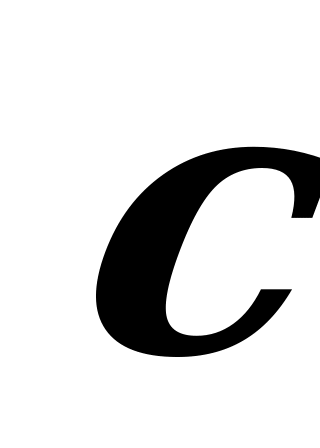 wektoryň moduly
wektoryň moduly  we
we 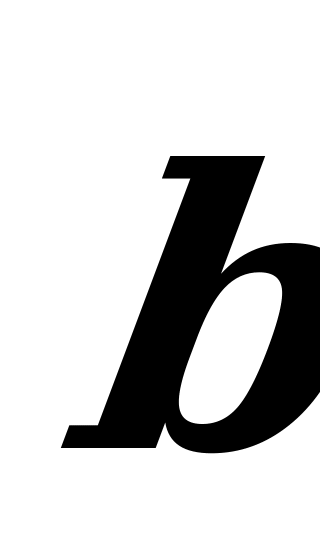 wektorlaryň üstünde gurlan parallelogramyň meýdanyna deňdir:
wektorlaryň üstünde gurlan parallelogramyň meýdanyna deňdir: 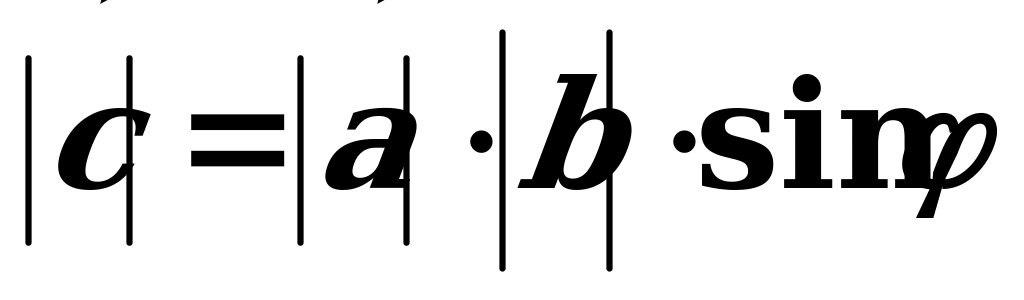 ;
; 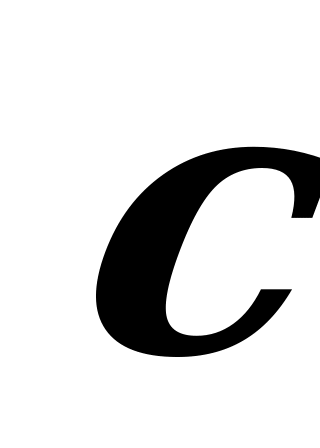 wektor
wektor  we
we 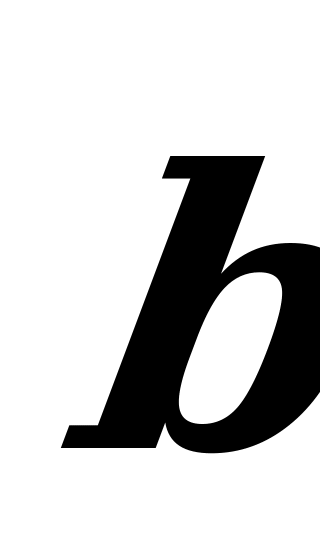 wektorlaryň her birine, diýmek olaryň ýatan tekizligine perpendikulýardyr:
wektorlaryň her birine, diýmek olaryň ýatan tekizligine perpendikulýardyr:  we
we 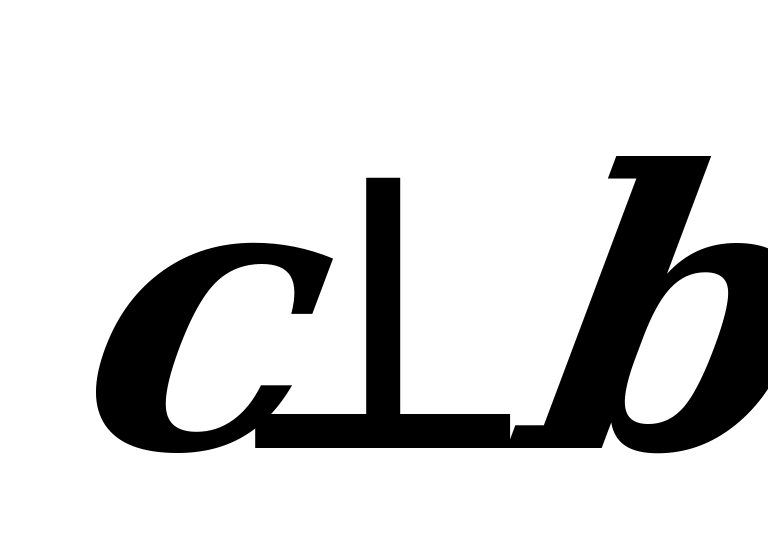 ;
;
Bir başlangyçdan alnyp goýlan  ,
, 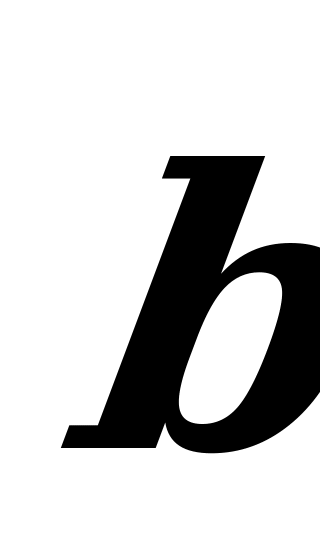 we
we 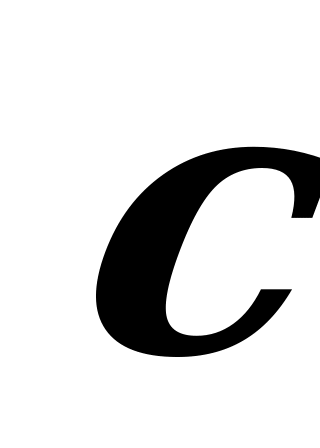 wektorlar wektorlaryň sagky üçlügini emele getirýärler
wektorlar wektorlaryň sagky üçlügini emele getirýärler

Wektorlar özara kollinear bolanda ýa-da birden-biri nul wektor bolsa, wektor köpeltmek hasyly nula deňdir. Wektoryň öz-özüne wektor köpeltmek hasyly nul wektora deňdir: 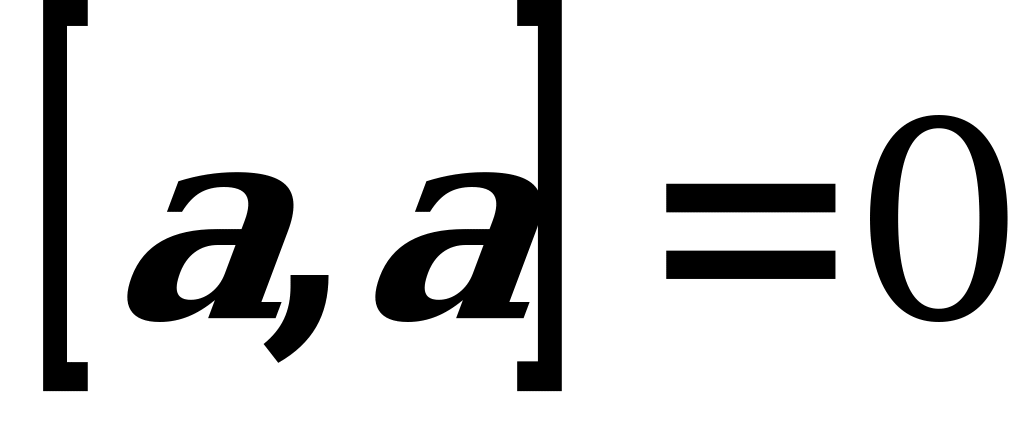 .
.
Eger  we
we 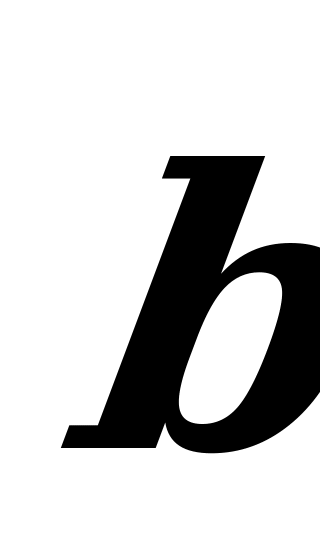 wektorlar giňişlikde, gönüburçly koordinatlar ulgamynda özleriniň
wektorlar giňişlikde, gönüburçly koordinatlar ulgamynda özleriniň 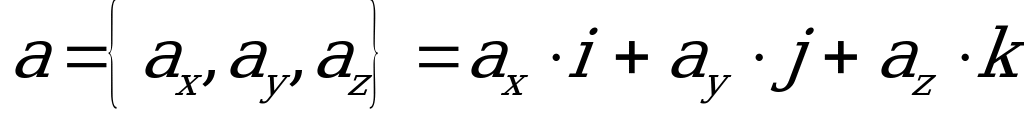 ,
,
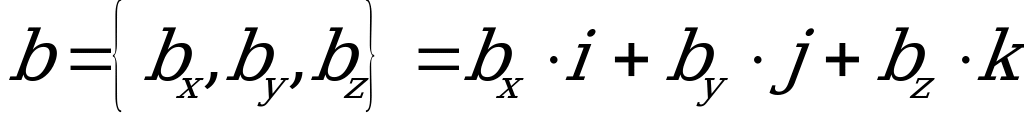 koordinatlary bilen berlen bolsa, onda olaryň wektor köpeltmek hasyly 3-nji tertipli kesgitleýji arkaly şeýle hasaplanylýar:
koordinatlary bilen berlen bolsa, onda olaryň wektor köpeltmek hasyly 3-nji tertipli kesgitleýji arkaly şeýle hasaplanylýar:
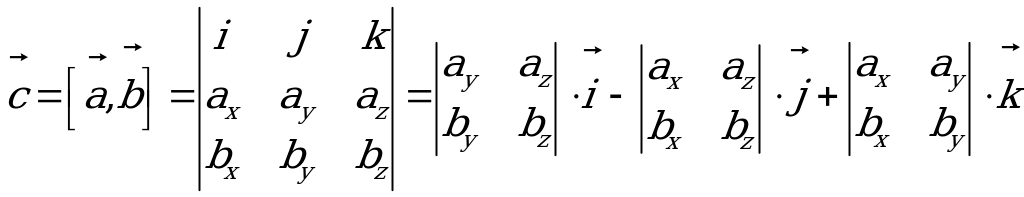
WEKTORLARYŇ GARYŞYK KÖPELTMEK HASYLY
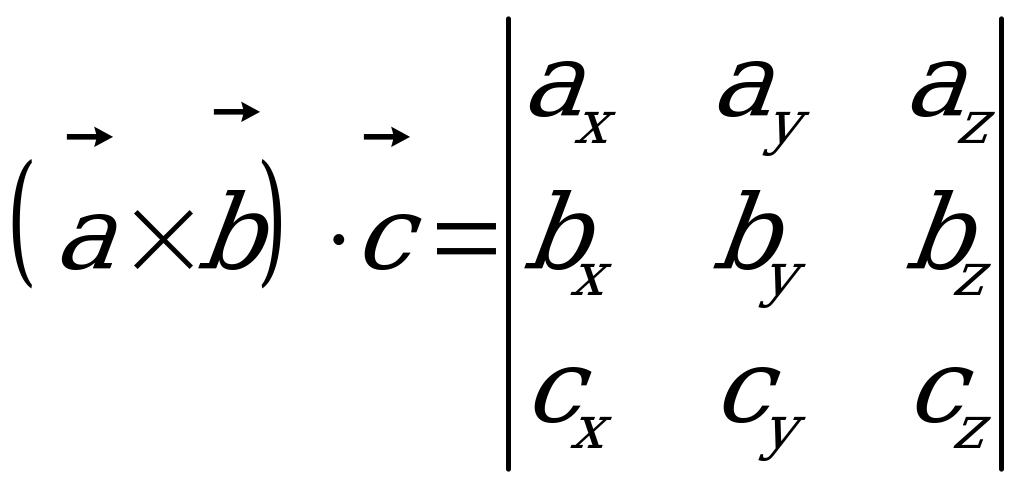






 .
.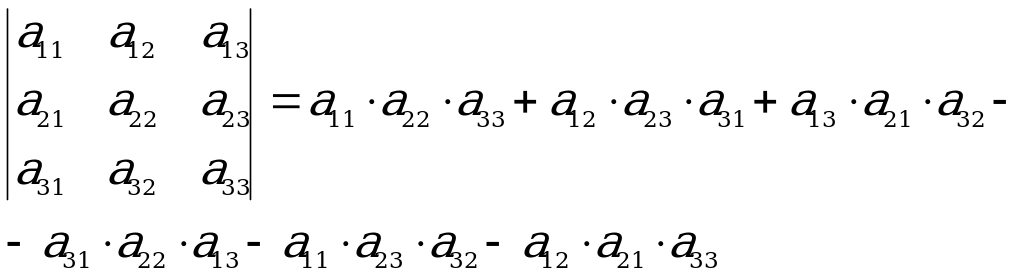
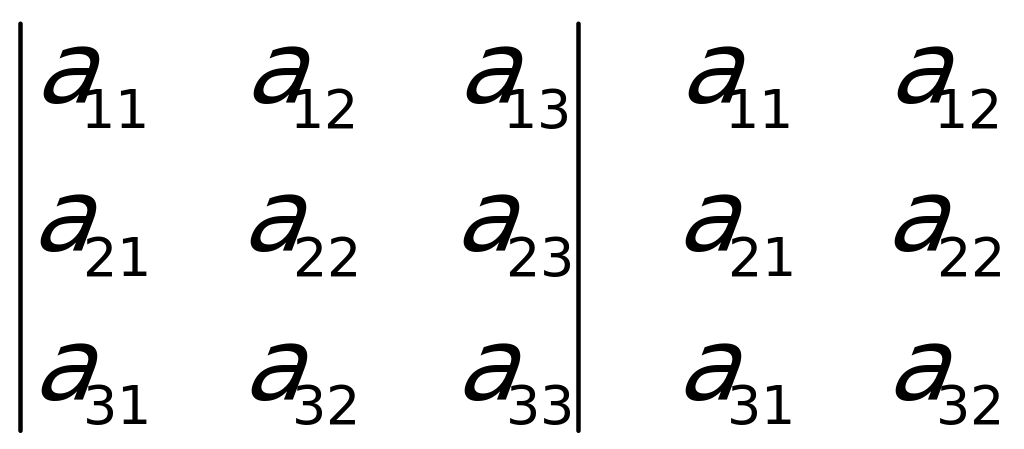
 .
.  .
.