Решение задач по теме:
«Вычисление расстояний и углов в пространстве»
Пример.
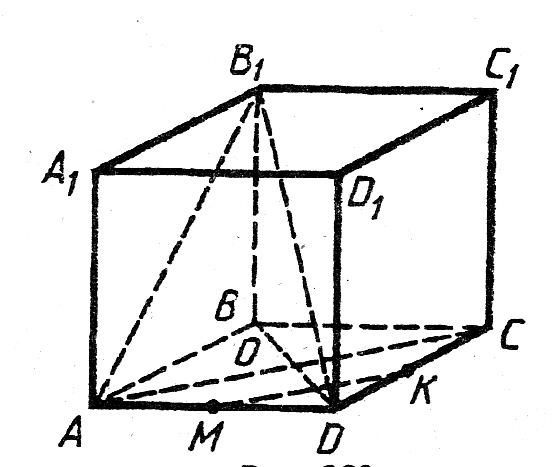 Дан куб АВСDА1В1С1D1. Ребро куба = а. Точка О – пересечение диагоналей АС и ВD. Точки М и К – середины ребер АD и CD соответственно.
Дан куб АВСDА1В1С1D1. Ребро куба = а. Точка О – пересечение диагоналей АС и ВD. Точки М и К – середины ребер АD и CD соответственно.
1. Найти расстояния:
-
от точки А до плоскости (А1В1С1);
-
от точки С до плоскости (ВDD1);
-
между прямыми АА1 и ВС;
-
между прямыми АС и ВВ1.
2. Найти углы:
-
между прямой В1D и плоскостью (АВС);
-
между прямыми В1D и АА1;
-
двугранный угол АDD1В (угол с ребром DD1 и гранями АDD1 и DD1В).
Решение:
1.
Расстоянием от точки до плоскости называется длинна перпендикуляра, опущенного из этой точки на плоскость.
-
Расстояние от точки А до плоскости (А1В1С1) – длина отрезка АА1. По условию АА1=а.
-
Расстояние от точки С до плоскости (ВDD1) – длина отрезка СО. СО = ½ СА. Зная ребро куба, по Т. Пифагора: СА = 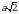 . Тогда СО =
. Тогда СО = 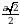 .
.
Расстояние между скрещивающимися прямыми – это длина их общего перпендикуляра.
-
АА1 и ВС – скрещивающиеся. АВ – их общий перпендикуляр. По условию АВ=а.
-
АС и ВВ1 – скрещивающиеся. ОВ – их общий перпендикуляр. Зная ребро куба, по Т. Пифагора: ВD = 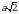 . Тогда ВО =
. Тогда ВО = 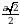 .
.
2.
а) Угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость.
ВD – проекция В1D на плоскость (АВС).
Найдем угол между В1D и ВD.
Рассмотрим треугольник В1ВD. В нем угол В прямой, ВВ1 = а, ВD = 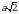 . Угол В1DВ - ?
. Угол В1DВ - ?
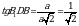 .
.
б) Угол между скрещивающимися прямыми – это угол между пересекающимися параллельными им прямыми.
В1D и АА1 - скрещивающиеся.
ВВ1 параллельна АА1 и пересекается с В1D. Значит угол между прямыми В1D и АА1 равен углу между прямыми В1D и ВВ1.
Рассмотрим треугольник В1ВD. В нем угол В прямой, ВВ1 = а, ВD = 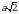 . Угол ВВ1D - ?
. Угол ВВ1D - ?
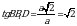
в) Мерой двугранного угла является мера его линейного угла. Линейный угол двугранного угла ищут в плоскости, перпендикулярной его ребру.
Угол АDВ является линейным углом двугранного угла АDD1В.
Рассмотрим треугольник АВD. В нем угол А прямой, ВА = АD = а. Угол АDВ - ?
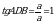 . Угол АDВ = 45˚.
. Угол АDВ = 45˚.
Самостоятельно:
Вычисление расстояний.
-
Устно. Что называется расстоянием между параллельными прямыми? скрещивающимися прямыми?
-
Начертите куб. Постройте общий перпендикуляр:
-
двух скрещивающихся ребер куба (выбрать самим любые скрещивающиеся ребра);
-
диагонали грани и ребра, не пересекающего эту диагональ, например, АВ1 и СС1;
-
диагонали куба и ребра, не пересекающего эту диагональ, например, DВ1 и СС1.
-
Укажите какие отрезки определяют расстояние между нижеперечисленными прямыми и найдите их длину:
-
А1В1 и СС1
-
В1D1 и AB
-
АА1 и В1D1
-
АС и В1D1
-
МК и DD1
-
Устно. Что называется расстоянием между точками? от точки до прямой? от точки до плоскости?
-
Укажите какие отрезки определяют расстояние между нижеперечисленными точками и плоскостями и найдите их длину:
-
от С до (BDD1)
-
от О до (DСС1)
-
от центра куба до точки А
Вычисление углов.
-
Устно. Что называется углом между прямой и плоскостью?
-
Вычислить угол между прямой и плоскостью:
-
ВD и (В1АВ)
-
В1D и (В1АВ)
-
Устно. Что называется углом между скрещивающимися прямыми?
-
Вычислить угол между скрещивающимися прямыми:
-
АС и А1D1
-
МК и СС1
-
Устно. Что такое линейный угол двугранного угла?
-
Вычислить двугранный угол:
-
АВВ1С
-
АВВ1D
-
КАА1D
Задания выполнить в рабочей тетради. Решение задач сопровождать чертежами.







 Дан куб АВСDА1В1С1D1. Ребро куба = а. Точка О – пересечение диагоналей АС и ВD. Точки М и К – середины ребер АD и CD соответственно.
Дан куб АВСDА1В1С1D1. Ребро куба = а. Точка О – пересечение диагоналей АС и ВD. Точки М и К – середины ребер АD и CD соответственно.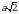 . Тогда СО =
. Тогда СО = 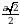 .
.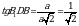 .
.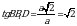
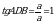 . Угол АDВ = 45˚.
. Угол АDВ = 45˚.

















